Álgebra Tutoriais

Assíntotas horizontais

Neste tutorial abordaremos o conceito de subida horizontal e suas aplicações mais importantes. Tentaremos evitar explicações excessivamente técnicas, mas serão utilizados alguns toques de Cálculo.

Principalmente, a parte importante deste tutorial é uma forte intuição geométrica sobre assíntotas horizontais. Vamos começar!

O que é uma assíntota horizontal

Uma Assíntota Horizontal é um limite superior, que você pode imaginar como uma linha horizontal que estabelece um limite para o comportamento do gráfico de uma determinada função.

Isso significa que o gráfico da função \(f(x)\) se aproxima dessa linha horizontal, à medida que o valor de \(x\) aumenta.

Como você encontra a assíntota horizontal?

Compreender este comportamento horizontal limitante de funções que apresentam esta característica pode ser muito útil para encontrar assíntotas horizontais.

Na verdade, em certas circunstâncias, esse comportamento limitante se parece bastante com o de uma linha horizontal para valores grandes de \(x\). Veja a função abaixo, por exemplo.

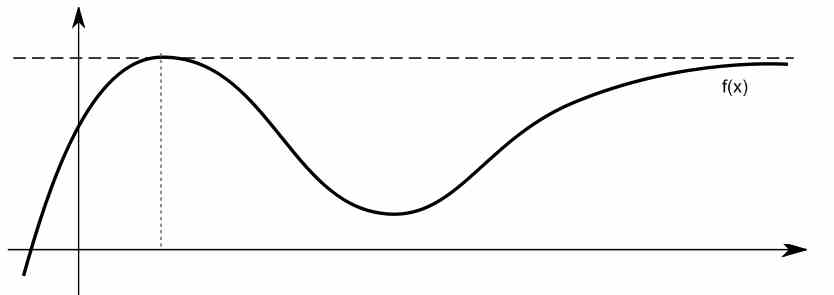
Como você encontra a assíntota horizontal de uma função usando limites?

Para deixar a definição clara, uma linha horizontal \(y = h\) é uma assíntota horizontal da função \(f(x)\) se

\[\large \lim_{x\to\infty} f(x) = h\]

se o limite acima existe e é finito. Para quem ainda não fez aula de cálculo, a reta horizontal \(y = h\) é uma assíntota horizontal da função \(f(x)\) quando \(h\) é o limite de \(f(x)\) conforme \(x\) se aproxima do infinito. O que significa ser um “limite”? Isso significa que para valores suficientemente grandes de \(x\), o valor de \(f(x)\) será tão próximo de \(h\) quanto predeterminamos. Fantasia, certo?

Qual é a fórmula da assíntota horizontal?

Para determinar a fórmula da assíntota horizontal, primeiro precisamos de determinar o limite correspondente. Suponha que você tenha

\[\large \lim_{x\to\infty} f(x) = h\]

Nesse caso, diremos que a assíntota horizontal é \(h\), e a fórmula para a assíntota horizontal é \(y = h\). Em outras palavras, a assíntota horizontal é simples é a reta horizontal, esta é uma reta com inclinação zero.

Isso dá sentido ao que significa uma assíntota horizontal em termos de limites: o limite encontrado corresponde a definir a linha horizontal que é chamada de assíntota horizontal.

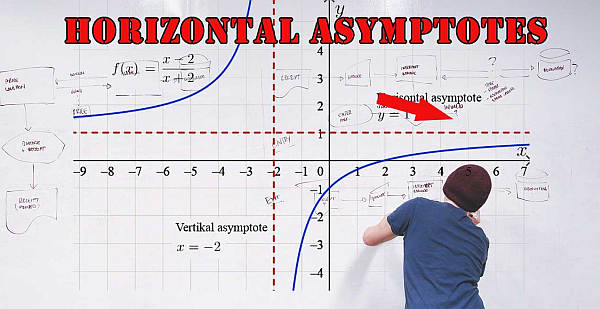
Exemplo 1

Encontre uma assíntota horizontal para a função

\[ \large f(x) = \frac{x^2}{x^2+1} \]

Resposta:

Para encontrar a assíntota horizontal, precisamos encontrar o limite da função \(f(x)\) à medida que \(x\) se aproxima do infinito. Se você não está familiarizado com Cálculo, você deve primeiro tentar avaliar a função com um valor muito grande de \(x\).

Por exemplo, digamos que \(x = 1,000,000\). Vamos inserir esse número na função:

\[ \large f(1,000,000) = \frac{1,000,000^2}{1,000,000^2+1} = \frac{1,000,000,000,000}{1,000,000,000,000+1}\] \[ = \frac{1,000,000,000,000}{1,000,000,000,001} = 0.999999999999 \]

que é muito próximo de 1. Então, deve-se suspeitar que o limite é 1. Na verdade, acontece que quando \(x\) é grande, o valor de \(x^2\) é tão grande em relação a 1, que \(x^2\) é muito semelhante a \(x^2 + 1\), pelo menos em termos relativos. Então temos, dividindo o numerador e o denominador por \(x^2\):

\[ \large f(x) = \frac{x^2}{x^2+1} = \frac{1}{1+\frac{1}{x^2}} \rightarrow \frac{1}{1+0} = 1 \]

porque \(\frac{1}{x^2}\) se aproxima de 0 enquanto \(x\) se aproxima do infinito. Portanto, não é difícil provar ou estar convencido de que

\[\large \lim_{x\to\infty} f(x) =\large \lim_{x\to\infty} \frac{x^2}{x^2+1} = 1\]

o que significa que a assíntota horizontal é \(y = 1\). Agora, tome cuidado com sua resposta se estiver respondendo a uma prova ou lição de casa. Algumas pessoas dirão “a assíntota horizontal é 1”, o que está errado.

Tecnicamente, a assíntota horizontal é a função \(y = 1\), e NÃO o número 1. A assíntota horizontal é uma função constante, que não é o mesmo que um número. Só estou dizendo, porque existem alguns alunos exigentes por aí.

Exemplo 2

Encontre uma assíntota horizontal, se existir para a função

\[ \large f(x) = \frac{x^3}{x^2+1} \]

Resposta:

Dividindo o numerador e o denominador por \(x^2\):

\[ \large f(x) = \frac{x}{1+\frac{1}{x^2}} \]

Mas espere! O truque não funcionou aqui? Sim, aconteceu. Observe que o denominador ficará muito próximo de 1 à medida que \(x\) se tornar muito grande, e o numerador ficará muito grande.

Não é difícil acreditar que \(f(x)\) converge para o infinito, de modo que não existe uma assíntota horizontal. Sempre que vemos uma função ilimitada, como é o caso de \(f(x)\) neste exemplo, não teremos uma assíntota horizontal.

Assíntota horizontal ou assíntota horizontal?

Tecnicamente, poderia haver duas assíntotas horizontais, uma à esquerda e outra à direita. A assíntota horizontal esquerda é \(y = h_L\) se

\[\large \lim_{x \to -\infty} f(x) = h_L\]

Da mesma forma, a assíntota horizontal direita é \(y = h_R\) se

\[\large \lim_{x \to +\infty} f(x) = h_R\]

caso algum dos limites acima exista e seja finito. Pode acontecer que uma função tenha duas assíntotas horizontais, tenha apenas uma assíntota horizontal ou não tenha nenhuma.

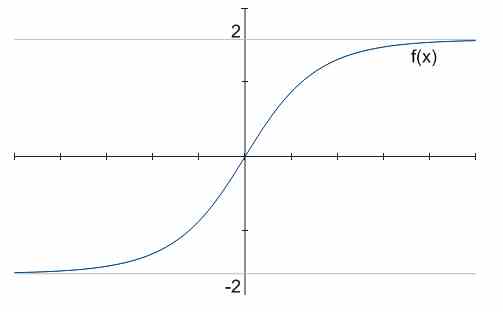
Por exemplo, no gráfico acima, existem duas assíntotas horizontais, \(y = -2\) e \(y = 2\).

Qual é a regra para encontrar a assíntota horizontal?

Não existem regras gerais que funcionem para todos os casos. No caso geral, precisamos calcular o limite quando \(x\) se aproxima de \(-\infty\), e o limite quando \(x\) se aproxima de \(+\infty\).

Se algum desses limites existir e for finito, teremos as assíntotas horizontais.

Uma regra específica pode ser desenvolvida para o caso em que a função dada \(f(x)\) é o quociente de dois polinômios. Se for esse o caso, vamos supor que \(m\) seja a ordem do polinômio no numerador e \(n\) seja a ordem do polinômio no denominador. Então temos os seguintes casos:

Caso 1: Se \(m < n\), então a assíntota horizontal é \(y = 0\).

Caso 2: Se \(m = n\) e \(a\) for o coeficiente inicial do polinômio no numerador e \(b\) for o coeficiente inicial do polinômio no denominador, então a assíntota horizontal será \(\displaystyle y = \frac{a}{b}\).

Caso 3: Se \(m > n\), então não há assíntota horizontal.

Exemplo 2

Encontre, se existir, a assíntota horizontal da função

\[\large f(x) = \frac{3x^2+2x-1}{2x^2 -x+2}\]

Resposta:

A função consiste no quociente de dois polinômios. O polinômio no numerador é \(3x^2+2x-1\), que é um polinômio de ordem 2, então \(m = 2\) e coeficientes iniciais 3.

O polinômio no denominador é \(2x^2 -x+2\), que é um polinômio de ordem 2, então \(n = 2\) e constante inicial 2. Você pode usar nosso calculadora polinomial para realizar esta divisão mostrando todos os passos.

Portanto, como neste caso \(m = n\), existe uma assíntota horizontal, e é o quociente dos coeficientes líderes, então, neste caso, a assíntota horizontal é

\[\large y = \frac{3}{2}\]

Mais sobre assíntotas horizontais

Então sua pergunta é como encontrar assíntotas de uma equação, certo? Primeiro de tudo, você encontra assíntotas de um função , não de uma equação. Então, você precisa começar com a definição geral, usando limites.

Se você não conhece cálculo e não sabe como calcular limites, então você deveria pelo menos tentar inserir valores muito grandes de \(x\), e também valores muito negativos de \(x\) na função, e ver como o função se comporta.

Até mesmo traçar a função com algum software pode dar uma dica clara se existem assíntotas horizontais.

Em última análise, no caso muito restrito em que a função é uma quociente de polinômios , então você pode aplicar a regra com base nos pedidos \(m\) e \(n\).