Regole degli esponenti
Le operazioni con esponenti sono tra le operazioni più comuni che eseguirai in tutto il mondo in matematica ed è fondamentale che tu abbia una base adeguata su di esse.
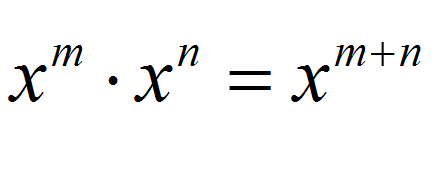
Senza ulteriori indugi, elenchiamo le proprietà di base degli esponenti. L'uso efficiente di queste proprietà è della massima importanza. Le regole sono:
Regola 1: \(\large \displaystyle x^0 = 1\), per \(x = \not 0\)
Regola 2: \(\large\displaystyle x^1 = x\)
Regola 3: \(\large\displaystyle x^m \cdot x^n = x^{m+n}\)
Regola 4: \(\large\displaystyle \left(x^m\right)^n = x^{mn}\)
Regola 5: \(\large\displaystyle \frac{x^m}{x^n} = x^{m-n}\)
Regola 6: \(\large\displaystyle (x \cdot y)^m = x^m \cdot y^m\)
Spieghiamo un po 'queste regole in parole .
Regola 1
sta dicendo che qualsiasi cosa elevata alla potenza di zero è uguale a 1. Bene, tranne 0, perché per convenzione (e c'è una buona ragione per questo) \(0^0 = 0\).
Adesso,
Regola 2
sta dicendo che prendendo un numero qualsiasi e elevandolo alla potenza di 1 si ottiene lo stesso numero originale. In altre parole, elevare un numero alla potenza di 1 non influisce sul numero.
Regola 3
sta dicendo che quando moltiplico potenze con la stessa base, il risultato è una potenza che ha la stessa base, elevata ad una potenza che corrisponde alla somma degli esponenti delle potenze che sto moltiplicando.
Regola 4
sta dicendo che prendere la potenza di una potenza è lo stesso che prendere una potenza con gli esponenti moltiplicati come esponente.
Regola 5
sta dicendo che quando divido potenze con la stessa base, il risultato è una potenza che ha la stessa base, elevata ad una potenza che corrisponde alla sottrazione degli esponenti delle potenze che sto moltiplicando.
Regola 6
sta dicendo che quando ho un potere che influenza una moltiplicazione, allora è come moltiplicare ciascuno dei termini elevati a quel potere.
ESEMPIO 1
Semplifica la seguente espressione
\[\large \displaystyle \frac{x^{3}y^{3}}{\sqrt x y^2}\]RISPOSTA:
Utilizzo della regola 5 per la divisione dei poteri con la stessa base:
\[\large \displaystyle \frac{x^{3}y^{3}}{\sqrt x y^2} = \frac{x^{3}y^{3}}{x^{1/2} y^2} \] \[\large \displaystyle = \frac{x^3}{x^{1/2}} \cdot \frac{y^3}{y^2} = \displaystyle x^{3-1/2} \cdot y^{3-2}\] \[\large \displaystyle = \displaystyle x^{5/2} \cdot y^{1} = x^{5/2} y\]Dovrei preoccuparmi degli esponenti negativi?
Non proprio. Prima di tutto, le 5 regole per gli esponenti sopra indicate non fanno alcuna dichiarazione specifica sul fatto che gli esponenti debbano essere non negativi. Infatti le regole funzionano lo stesso degli esponenti sono negativi.
Infatti, per esponenti negativi , ci saranno due regole che ti permetteranno di trasformarle in esponenti positivi:
\[\large\displaystyle \frac{1}{x^n} = x^{-n}\]
Questa espressione sopra ci mostra che possiamo convertire una potenza con un esponente negativo che è nel numeratore in una potenza nel denominatore con il corrispondente esponente positivo.
Questa espressione sopra ci mostra che possiamo convertire una potenza con un esponente negativo che è nel denominatore in una potenza al numeratore con il corrispondente esponente positivo.
ESEMPIO 2
Semplifica la seguente espressione, senza lasciare esponenti negativi:
\[\large \displaystyle \frac{x^{4}\sqrt{x} y^{-2}}{x^{-3/2} y^{1/2}}\]RISPOSTA:
Trasformare gli esponenti negativi in esponenti positivi e applicare le 5 regole degli esponenti:
\[\large \displaystyle \frac{x^{4}\sqrt{x} y^{-2}}{x^{-3/2} y^{1/2}} = \frac{x^{4} x^{1/2} y^{-2}}{x^{-3/2} y^{1/2}} \] \[\large \displaystyle = \frac{x^{4} x^{1/2} x^{3/2}}{y^{1/2} y^{2}} = \frac{x^{4+1/2+3/2}}{y^{2+1/2}} \] \[\large \displaystyle = \frac{x^{6}}{y^{5/2}} \]che conclude la semplificazione.
Queste regole degli esponenti sono in qualche modo correlate alle regole dei logaritmi?
Assolutamente! Controlla il regole logaritmiche e scoprirai che sono strutturalmente molto simili, e questo perché i logaritmi e le potenze sono operazioni inverse tra loro.
Solo come un piccolo esempio, facciamo una rapida dimostrazione. Supponiamo che \(a = x^m\) e \(b = x^n\). Quindi, per definizione, \(m = \log_x a\) e \(n = \log_x b\). Quindi, secondo le regole dell'esponente, \(a\cdot b = x^m \cdot x^n = x^{m+n}\). Quindi, per definizione, \(m + n = \log_x (a \cdot b)\). Ma \(m = \log_x a\) e \(n = \log_x b\), quindi \(\log_x a + \log_x b = \log_x (a \cdot b)\).
Ulteriori informazioni sulla regola degli esponenti
Una cosa su cui dobbiamo porre l'accento è sul fatto che le regole per gli esponenti non richiedono che gli esponenti siano positivi. Non è necessario che gli esponenti siano interi. Le regole valgono per gli esponenti reali.
• Non dimenticare che se hai a che fare con un esponente negativo al numeratore, puoi trasformarlo passandolo al denominatore con esponente positivo.
• Inoltre, se hai a che fare con un esponente negativo al denominatore, puoi trasformarlo passandolo al numeratore con esponente positivo.
Le regole degli esponenti hanno così tante applicazioni, incluso fornire una base per ottenere il regole per semplificare i radicali , che vengono come corollario delle radici degli esponenti.
In termini grafici, puoi esplorare questa regola con rappresentare graficamente diverse funzioni esponenziali e vedendo le proprietà specifiche che hanno.