Regole di registro
La funzione logaritmica è una delle funzioni più importanti in matematica e le regole di log sono semplici e convenienti, rendendo davvero facile lavorare con i logaritmi.
Ricordiamo innanzitutto qual è il significato di \(\log_b a\). In questo contesto, il valore \(b\) è il base del logaritmo e \(a\) è il discussione .
Diciamo che \(\log_b a = y\) quando \(b^y = a\). Questo sta dicendo che \(\log_b a\) è il numero a cui deve essere elevato \(b\) (la base) per ottenere \(a\) (l'argomento).
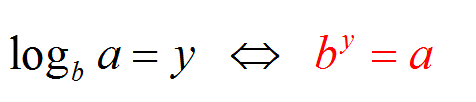
Ad esempio, \(\log_{10} 25\) corrisponde al numero a cui devo aumentare 10 per ottenere 25. Quindi il logaritmo che sto cercando è il numero \(y\) che ha la proprietà che \(10^y = 25\)
Ora la domanda è: come calcoliamo quel numero \(y\) che ha la proprietà \(10^y = 25\)? Bene, quel numero è ben definito e la funzione logaritmica \(f(x) = \log_{10} x\) se ne occupa. Questa funzione non è una funzione elementare e per rappresentarla è necessaria una serie di Taylor (serie infinita).
Oppure puoi usare una calcolatrice (che probabilmente è più facile, giusto?).
Le regole del registro: proprietà dei logaritmi
Queste sono le principali regole di registro:
Regola n. 1 : \(\large \log_a (b\cdot c) = \log_a (b)+ \log_a (c) \)
Regola n. 2 : \(\large \displaystyle \log_a \frac{b}{c} = \log_a (b) - \log_a (c) \)
Regola # 3 : \(\large \log_a (b^c) = c \cdot \log_a (b) \)
Regola # 4 : \(\large \log_a (a) = 1 \)
Regola n. 5 : \(\large \log_a (1) = 0 \)
ESEMPIO 1
Semplifica \(\log_2 8 + \log_2 4\) utilizzando le regole di registro:
RISPOSTA:
Usando la regola n. 1, troviamo che:
\[ \log_2 8 + \log_2 4 = \log_2 (8 \cdot 4) = \log_2 32 = 5\]Quindi, il primo passo è una semplice applicazione della Regola # 1, ma come otteniamo \(\log_2 32 = 5\)? È perché \(2^5 = 32\), quindi in questo caso troviamo direttamente qual è il numero che devi aumentare \(2\) per ottenere \(32\).
Per la maggior parte dei logaritmi avrai bisogno di una calcolatrice per calcolarli. Sono solo pochi selezionati che puoi calcolare direttamente. Cose come \(\log_{10} 100 = 2\), perché sai facilmente che \(10^2 = 100\).
Ma puoi calcolare \(\log_{10} 102\) direttamente? Non proprio, hai bisogno di una calcolatrice per questo.
ESEMPIO 2
Esprimi la somma e la sottrazione dei logaritmi: \( \displaystyle \log_{10} \sqrt[3]{\frac{a}{6bc}} \).
RISPOSTA:
Prima di tutto, dobbiamo ricordare che prendere una radice cubica è come elevare alla potenza \(1/3\). In altre parole, \(\sqrt[3]{x}\) è uguale a \(x^{1/3}\).
Quindi, prima usiamo la Regola # 3 per portare la potenza davanti al logaritmo, e poi usiamo le Regole # 1 e # 2. Noi abbiamo:
\[ \displaystyle \log_{10} \sqrt[3]{\frac{a}{6bc}} \] \[= \displaystyle \log_{10} \left({\frac{a}{6bc}}\right)^{1/3} \] \[= \displaystyle \frac{1}{3} \log_{10} \frac{a}{6bc} \] \[= \displaystyle \frac{1}{3} \left( \log_{10} a - \log_{10} (6bc) \right) \] \[= \displaystyle \frac{1}{3} \left( \log_{10} a - \log_{10} 6 - \log_{10} b - \log_{10} c \right) \]che è ciò che era richiesto: somma e sottrazioni di logaritmi semplici.
Il cambiamento della formula di base per i logaritmi
Una delle formule più utili relative ai logaritmi è il cambio di formula di base. Questa formula funziona così:
\[ \large \displaystyle \log_c a = \frac{\log_b a}{\log_b c}\]Questa formula sta solo dicendo che se vuoi cambiare la base da \(b\) a \(c\), i risultati sono essenzialmente gli stessi, ma devi dividere per il logaritmo della nuova base.
Ora, se sei orientato artisticamente, puoi goderti la forma alternativa del cambio di formula basato espresso di seguito:
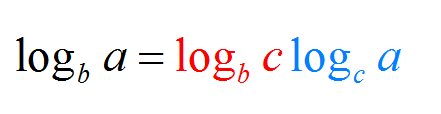
ESEMPIO 3
Esprimi il logaritmo naturale \(\ln\) in termini di \(\log\) (base 10).
RISPOSTA:
Usando il cambio di formula di base, otteniamo che:
\[ \large \displaystyle \ln a = \log_e a = \frac{\log_{10} a}{\log_{10} e} =\frac{\log a}{\log e} \]Quindi stai dicendo che \(\ln a\) si ottiene dividendo \(\log a\) per \(\log e\). Quanto conveniente? Chi ha detto che la matematica è stata difficile, eh?
Ulteriori informazioni sulle regole di registro
I logaritmi sono molto importanti in matematica. Storicamente, i logaritmi svolgono un ruolo molto importante nell'astronomia, come un modo per prevedere il movimento della luna e dei pianeti.
Le funzioni logaritmiche stanno al centro di tutto in Math, si intrecciano con esponenziali, esponenti e praticamente tutto. Ecco perché ti chiedono di imparare i logaritmi a memoria, perché sono importanti.
Inoltre, queste regole di registro presentate qui svolgono un ruolo cruciale nel facile il risoluzione di equazioni logaritmiche .
Convenzioni di notazione
Ci sono un paio di convenzioni di notazione che devi conoscere. In generale, scriviamo \(\log_b a\) e lo diciamo "logaritmo in base b di a". Quando la base è \(b = 10\), per convenzione scriviamo semplicemente \(\log a\). Quindi, quando vedi un \(\log\) senza una base, si presume che la base sia \(10\).
C'è un altro caso degno di nota. Per \(\log_b a\), quando la base è \(b = e\) (la costante di Eulero), scriviamo \(\ln a\) invece di \(\log_e a\). Quindi, quando viene utilizzato \(\ln\) invece di \(\log\), è perché la base del logaritmo è \(e\).
Si noti che \(\ln a\) viene visualizzato come indicato registro naturale . E sì, i log naturali hanno le stesse regole del log generale.
Se hai una funzione logaritmica che vorresti rappresentare graficamente, puoi provare il nostro Creatore di grafici di funzioni logaritmiche , che ti fornirà un grafico ben presentato.
