La parabola.
Una parabola è il luogo geometrico dei punti negli assi delle coordinate che hanno la proprietà che sono equidistanti da un punto fisso (chiamato focus) e una linea (chiamata Directrix).
So cosa sembra un po 'troppo tecnico, ma andremo attraverso di esso, e alla fine vedrai che non è così difficile.
Quindi, aiuterebbe se l'avessi detto
La Funzione \(f(x) = x^2\) Rappresenta UNA PARABLA?
Sicuro che aiuterà.E potresti pensare "perché non mi hai detto fin dall'inizio che la parabola è quella funzione?".
Perché non c'è una parabola, c'è un numero infinito di loro.E una parabola non deve nemmeno essere rappresentata da una funzione.Sì, alcune relazioni sono parabolas, come vedremo.
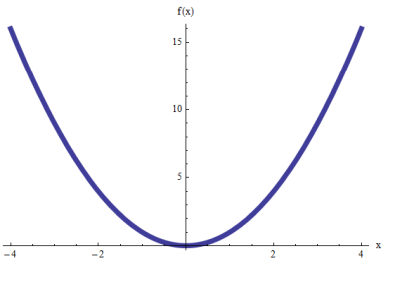
Una cosa è importante da ricordare: Utilizzando funzioni e relazioni, ci sono i parabole che "aprono" lungo l'asse \(y\)-asse, e ci sono i parabole che "aprivano" lungo l'asse \(x\)-Axis.
Alla fine, per simmetria, è facile rendersi conto che quei parabole che "aprivano" lungo l'asse Y hanno la stessa struttura di quelli che "aprono" lungo l'asse x, quindi è sufficiente sapere come impararegestire un tipo.
L'equazione generale della parabola
Ci sono semplici derivazioni per ottenere l'equazione di un parabola in base alla posizione di una Directrix e alla messa a fuoco, ma salteremo la derivazione in questa introduzione.
Controlla il grafico qui sotto.Dobbiamo identificare alcuni elementi cruciali della parabola: abbiamo il vertice, il focus e la directorrix.
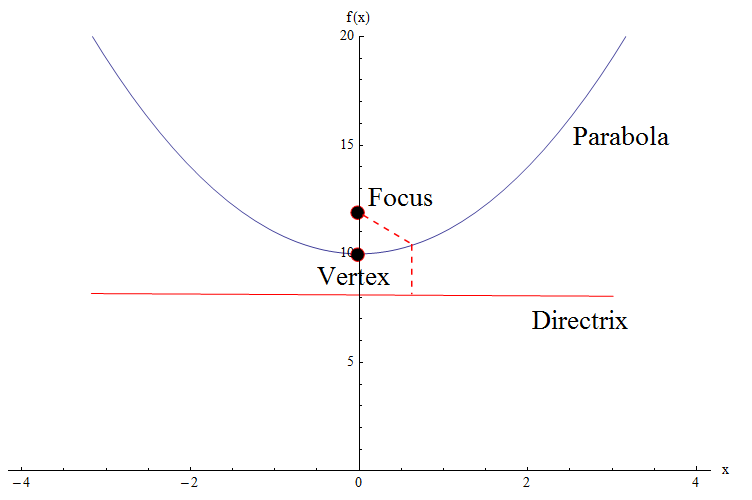
Non dovremmo molto dettagliare, ma diremo l'equazione di una parabola generale con vertice all'origine, con messa a fuoco \((0, a)\) e directrix uguale a \(y = -a\) è
Questa parabola è il tipo di parabola che si apre lungo l'asse Y.
Ora cosa succede quando invece di avere il vertice all'origine, vogliamo avere il vertice in un dato punto \((k,h)\)?
Bene, questa è la magia di lavorare con un sistema di coordinate, e tutto ciò che dobbiamo fare una traduzione dal punto punto \((k,h)\)?Ma come fai a una traduzione di \((k,h)\)?
Semplice!Ovunque tu abbia \(x\), lo sostituisci con \(x-k\), e ovunque tu abbia \(y\), lo sostituisci con \(x-h\).
Quindi, facendo una traduzione, l'equazione di una parabola generale con vertice al punto \((k,h)\), con focus \((k, h+a)\) e Directrix uguale a \(y = h-a\) è
\[\large y-h = 4a(x-k)^2\]che può essere scritto come
\[\large \boxed{ y = 4a(x-k)^2 + h }\]Cosa succede con i paraboli che si aprono lungo l'asse x?
Per simmetria, questo ha semplicemente ottenuto sostituendo i ruoli di \(x\) e \(y\) nell'equazione della parabola che abbiamo già.In praticità, ciò significa che ovunque \(x\) appare nell'equazione della parabola, lo abbiamo cambiato \(y\), e viceversa per \(y\).
Pertanto, l'equazione di una parabola generale con vertice al punto \((h,k)\), con focus \((h+a, k)\) e Directrix uguale a \(x = h-a\) è:
\[\large \boxed{ x = 4a(y-k)^2 + h }\]Notare la differenza:
Quando una parabola ha una directorrix del modulo \(y = -a\), allora la parabola si apre lungo l'asse y (su o giù a seconda che il focus sia sopra o sotto la Directrix).
Quando una parabola ha una directorrix del modulo \(x = -a\), quindi la parabola si apre lungo l'asse x (a sinistra oa destra a seconda che l'attenzione sia a sinistra oa destra della Directrix).
ESEMPIO 1
Trova l'equazione della parabola che ha una Directrix _ XYZ _ A _ e una messa a fuoco _ xyz_b _.Trova anche il vertice.
RISPONDERE:
Il vertice è il parabola sulla parabola, quindi è equidistante dalla Directrix \(y = -4\) e dalla messa a fuoco \((0, 4)\), quindi il vertice è \(0, 0)\).D'altra parte, per una parabola con vertice all'origine, l'equazione della directorrix è \(y = -a\), quindi in questo caso \(a = 4\).Di conseguenza, l'equazione della parabola è
\[ \large y = 4ax^2 = 4(4)x^2 = 16x^2 \]Graficamente:
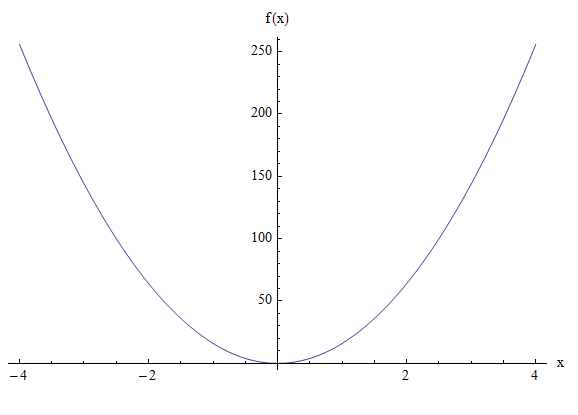
ESEMPIO 2.
Trova il vertice, la messa a fuoco e la directorrix della parabola \(y = 8x^2 - 16x + 9\).
RISPONDERE:
Prima di tutto, abbiamo bisogno di completare il quadrato:
\[\large y = 8x^2 - 16x + 9 = 8(x^2 - 2x) + 9 \] \[\large = 8(x^2 - 2x + 1 - 1) + 9 \] \[\large = 8(x^2 - 2x + 1) + 9 - 8 \] \[\large = 8(x-1)^2 + 1 \]L'equitazione con l'equazione generale, scopriamo che il vertice è al punto \((1, 1)\), e anche noi abbiamo quel \(4a = 8\), quindi \(a = 2\), quindi, la Directrix è \(y = h - a = 1 - 2 = -1\) e il focus è \((k, h + a) = (1, 1+2) = (1, 3)\).
Graficamente:
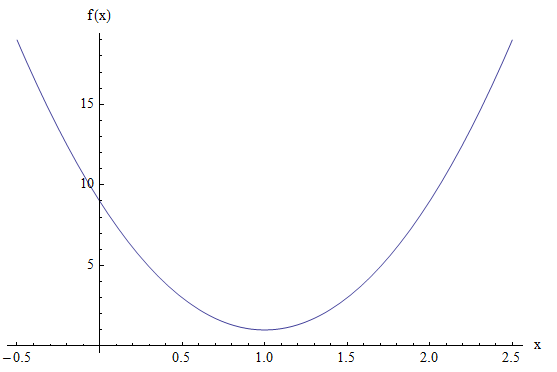
La parabola e le sezioni coniche generali
Strano come può essere, la parabola è strettamente correlata al cono.Come, diresti?Un matematico greco di nome Apollonius è di credito con aver contribuito con la versione moderna, utilizzando sistemi di coordinate, delle sezioni coniche.
Apollonius e altri matematici hanno scoperto che quando tagli un cono con un aereo, a seconda dell'angolo relativo del cono e del piano, il cono è tagliato in un modo che la sezione ha forme diverse.
Le diverse forme delle sezioni, a seconda dell'angolo relativo del taglio sono ciò che conosciamo come parabola, cerchio, ellisse e iperbole, come mostrato nella figura seguente:
Maggiori informazioni sulla parabola
Una parabola generale che si apre lungo l'asse y, con vertice all'origine \((0, 0)\) ha la seguente rappresentazione funzionale \(y = 4ax^2\).
Quindi, per simmetria, una parabola generale che si apre lungo l'asse x, con il vertice all'origine \((0, 0)\) ha la seguente rappresentazione funzionale \(x = 4ay^2\).
Quindi, un vertice generale può essere ottenuto applicando una traduzione a un determinato punto \((k, h)\).
Applicazioni
La parabola ha innumerevoli applicazioni in fisica, a causa del modo in cui la forza di gravità e le leggi di Newton operano, la traiettoria della maggior parte dei corpi che viene lanciata seguirà una traiettoria parabolica.
Inoltre, algebricamente parlando, i paraboli appaiono in algebra tutto il tempo, perché tutte le funzioni quadratiche hanno un grafico parabolico e le funzioni quadratiche appaiono molto in algebra.
Inoltre, i paraboli appaiono a calcolo quando trovi minimi e massimi.Si scopre che molti problemi di massimizzazione e di minimizzazione hanno una funzione quadratica per massimizzare e geometricamente, il massimo o il minimo (a seconda se la parabola si apre o verso il basso) viene raggiunta al vertice.
Altre sezioni coniche che potresti essere interessato a conoscere sono il Ellisse. , the Iperbole e il cerchio .