L'Ellisse
Un'ellisse è la posizione geometrica dei punti negli assi delle coordinate che hanno la proprietà che la somma delle distanze di un dato punto dell'ellisse a due punti fissi (i fuochi) è uguale a una costante, che denominiamo \(2a\).
Il concetto di "luogo geometrico" è molto interessante da un punto di vista concettuale, ma potrebbe non darti una visione chiara di ciò che stai cercando di rappresentare.
Prova a fare l'esercizio di guardare l'equazione qui sotto e vedi se riesci a capire come appare graficamente;
Potresti capire come funziona il grafico semplicemente guardando l'equazione sopra. Così ho pensato. Lascia che ti presenti l'ellisse:
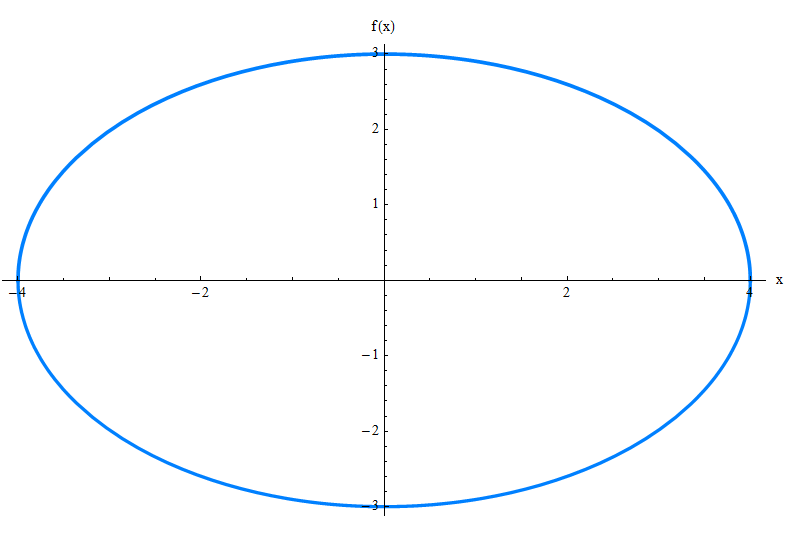
L'equazione generale dell'ellisse
Senza molta discussione teorica, affermeremo che l'equazione generale dell'ellisse con centro all'origine e con fuochi sull'asse x, per \(a \ge b\) è
\[\large \displaystyle \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 \]
Per l'ellisse sopra descritta, ha fuochi nei punti \((-c, 0)\) e \((c, 0)\), dove \(c = \sqrt{a^2 - b^2}\).
Ora cosa succede con l'equazione dell'iperbole sopra quando \(b > a\)?
In tal caso, i fuochi sono sull'asse y, e sono \((0, -c)\) e \((0, c)\), dove \(c = \sqrt{b^2 - a^2}\).
Ora, se volessimo spostare il centro in un punto \((k,h)\)?
Tutto quello che devi fare in questo caso è sostituire \(x\) con \(x-k\) e sostituire \(y\) con \(x-h\).
Quindi, facendo una traduzione, otteniamo che l'equazione di un'ellisse generale è
\[\large \boxed{\displaystyle \frac{(x-k)^2}{a^2} + \frac{(y-h)^2}{b^2} = 1 }\]L'ellisse sopra ha un centro in \((k,h)\) e ha fuochi in \((k-c, h)\) e \((k+c, h)\) dove \(c = \sqrt{a^2 - b^2}\) per \(a \ge b\) e \((k, h-c)\) e \((k, h+c)\) dove \(c = \sqrt{b^2 - a^2}\) per \(b>a\).
ESEMPIO 1
Trova i fuochi, dell'ellisse:
\[\large \displaystyle \frac{x^2}{9} + \frac{y^2}{16} = 1 \]RISPOSTA:
Innanzitutto, in base alla struttura dell'equazione precedente, l'ellisse è centrata all'origine \((0, 0)\). Si noti che il semiasse maggiore è 4, che è associato a \(9y\), quindi i fuochi si trovano sull'asse y.
Dall'equazione abbiamo ottenuto che \(a^2 = 9\) e \(b^2 = 16\). Troviamo che \(c = \sqrt{b^2 - a^2} = \sqrt{16 - 9} = \sqrt 7\). Pertanto, i fuochi sono in \((0, -\sqrt{7})\) e \((0, \sqrt{7})\).
ESEMPIO 2
Trova l'equazione dell'ellisse centrata su \((0, 2)\) con un focus su \((6, 2)\) e un semiasse minore con una dimensione di 3.
RISPOSTA:
Sulla base delle informazioni fornite, \(c = 6 - 0 = 6\). Poiché i fuochi sono paralleli all'asse x, otteniamo \(b = 3\) e quindi \(a = \sqrt{6^2 - 3^2} = \sqrt{27}\)
Quindi, l'equazione dell'ellisse è:
\[\large \displaystyle \frac{x^2}{27} + \frac{(y-2)^2}{9} = 1 \]L'ellisse e le sezioni coniche generali
Come nel caso della parabola, dell'iperbole e del cerchio, l'ellisse è strettamente correlata al cono. L'antico matematico greco di nome Apollonio ha scoperto questa connessione, con ciò che viene chiamato sezioni coniche .
Una sezione conica corrisponde alle forme che si quando si esegue un taglio attraverso un cono con un piano e, a seconda dell'angolo relativo del cono e del piano, la forma della sezione trasversale cambia.
Infatti, una seconda dell'angolo in cui il cono e il piano sono rivolti l'uno verso l'altro, la forma della sezione trasversale può essere una parabola, un cerchio, un'ellisse o un'iperbole. Questo è illustrato nel grafico sottostante:
Ulteriori informazioni sull'ellisse
Per un'ellisse con l'equazione \(\displaystyle \frac{x^2}{a^2} + \frac{y^2}{a^2} = 1 \), con \(a \ge b\), \(a\) è chiamato semiasse maggiore e \(b\) è chiamato semiasse minore.
Ora per \(b > a\), quella denominazione è invertita, quindi \(a\) verrebbe chiamato semiasse minore e \(b\) è chiamato semiasse maggiore.
Eccentricità
L'eccentricità di un'ellisse viene calcolata utilizzando la seguente formula:
\[\displaystyle e = \sqrt{1 - \left( \frac{b}{a}\right)^2}\]Questo parametro di eccentricità indica quanto la forma dell'ellisse si discosta da una versione simmetrica dell'ellisse (che è il cerchio, che ha eccentricità \(e = 1\)).
Applicazioni
L'ellisse ha così tante applicazioni. Nella scienza, è ampiamente utilizzato in astronomia. In effetti, i pianeti descrivono orbite ellittiche attorno al sole.
Algebricamente un'ellisse assomiglia molto a un'iperbole, ma le loro proprietà sono radicalmente diverse.
Potresti anche essere interessato a conoscere la parabola, per la quale puoi controllare questo tutorial . Puoi anche dare un'occhiata al nostro tutorial iperbole . Infine, puoi anche imparare tutto quello che c'è da fare conoscere il cerchio .