L'iperbole
Un'iperbole è il luogo geometrico dei punti negli assi delle coordinate che hanno la proprietà che la differenza tra le distanze di due punti fissi (i fuochi), è uguale a una costante, che chiamiamo \(2a\).
Naturalmente, suona un po 'intimidatorio e troppo tecnico, ma è davvero il modo in cui viene definita un'iperbole.
Forse, se ti dessi l'equazione di un'iperbole, la "riconosceresti".
Proviamo: questa è l'equazione di un'iperbole molto generale:
Puoi capire come appare controllando la sua equazione? Probabilmente no. Quindi presento l'iperbole, graficamente per te:
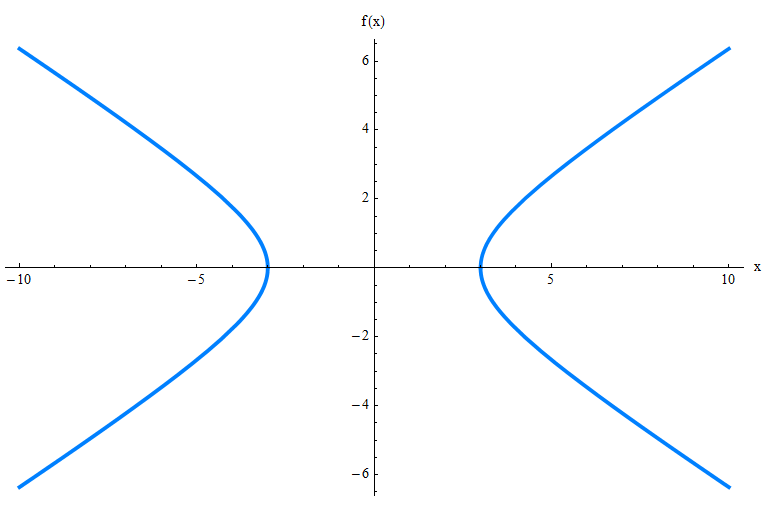
Il grafico sopra mostra solo il grafico dell'iperbole, ma ci sono molti altri elementi di cui devi essere consapevole, come gli asintoti inclinati, i vertici e i fuochi. Controlla il grafico sotto.
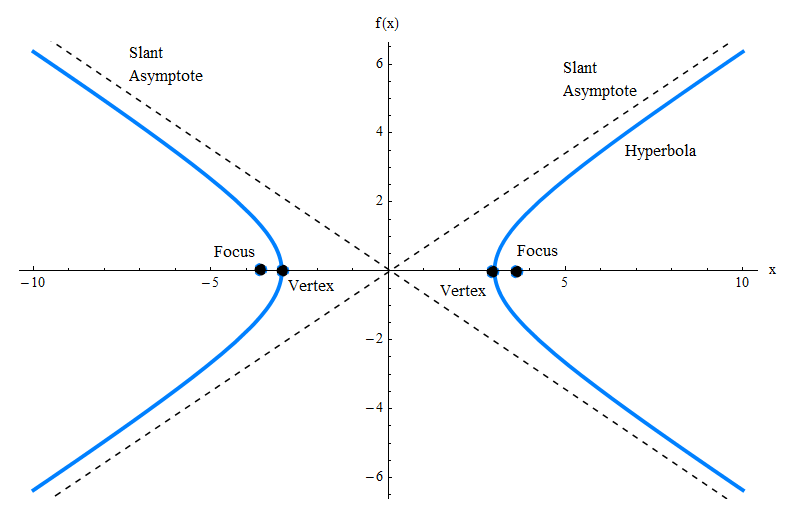
L'equazione generale dell'iperbole
Senza molta discussione teorica, affermeremo che l'equazione generale dell'iperbole con fuochi sull'asse x è
\[\large \displaystyle \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \]
Per l'iperbole descritta dall'equazione precedente, ha vertici nei punti \((-a, 0)\) e \((a, 0)\) e ha fuochi nei punti \((-c, 0)\) e \((c, 0)\), dove \(c = \sqrt{a^2 + b^2}\).
Una caratteristica interessante di questa iperbole è che ha due asintoti inclinati
Asintoto 1
: \(\displaystyle y = \frac{b}{a}x\)
Asintoto 2
: \(\displaystyle y = -\frac{b}{a}x\)
Ora cosa succede con l'equazione dell'iperbole, se invece i vertici vengono traslati di un dato punto \((k,h)\)?
Tutto quello che devi fare in questo caso è sostituire \(x\) con \(x-k\) e sostituire \(y\) con \(x-h\).
Quindi, facendo una traduzione, otteniamo che l'equazione di un'iperbole generale è
\[\large \boxed{\displaystyle \frac{(x-k)^2}{a^2} - \frac{(y-h)^2}{b^2} = 1 }\]L'iperbole di cui sopra ha vertici nei punti \((k-a, h)\) e \((k+a, h)\) e ha foci nei punti \((k-c, h)\) e \((k+c, h)\), dove \(c = \sqrt{a^2 + b^2}\).
Le equazioni degli asintoti di inclinazione sono \(y = \frac{b}{a}(x-k) + h\) e \(y = -\frac{b}{a}(x-k) + h\).
Cosa succede con le iperboli che si aprono lungo l'asse y?
Per simmetria, tutto ciò che dobbiamo fare è semplicemente sostituire i ruoli di \(x\) e \(y\) nell'equazione generale dell'iperbole che già abbiamo. In pratica, questo significa che ogniqualvolta \(x\) appare nell'equazione della parabola che abbiamo, lo cambiamo \(y\) e viceversa per \(y\).
Quindi, nel caso di un'iperbole che apre lungo l'asse x, l'equazione generale è
\[\large \boxed{\displaystyle \frac{(y-h)^2}{b^2} - \frac{(x-k)^2}{a^2} = 1 }\]L'iperbole di cui sopra ha vertici nei punti \((k, h - b)\) e \((k, h+b\) e ha foci nei punti \((k, h-c)\) e \((k, h+c)\), dove \(c = \sqrt{a^2 + b^2}\).
Le equazioni degli asintoti di inclinazione sono \(y = \frac{b}{a}(x-k) + h\) e \(y = -\frac{b}{a}(x-k) + h\).
ESEMPIO 1
Trova i fuochi, i vertici e gli asintoti obliqui dell'iperbole:
\[\large \displaystyle \frac{(y-2)^2}{9} - \frac{(x-4)^2}{16} = 1 \]RISPOSTA:
Questa iperbole si apre lungo l'asse y. In questo caso, i valori di traduzione sono \(k = 4\) e \(h = 2\). Inoltre, otteniamo \(a = \sqrt{16} = 4\) e \(b = \sqrt{9} = 3\). Quindi, otteniamo quel \(c = \sqrt{a^2+b^2} = \sqrt{4^2+3^2} = \sqrt{25} = 5\).
Quindi, i fuochi sono \((k, h-c) = (4, 2 - 5) = (4, -3)\) e \((k, h+c) = (4, 2 + 5) = (4, 7)\).
I vertici sono \((k, h-b) = (4, 2 - 3) = (4, -1)\) e \((k, h+b) = (4, 2 + 3) = (4, 5)\).
Gli asintoti inclinati sono
\[\displaystyle y = \frac{b}{a}(x-k) + h = \frac{3}{4}(x-4) + 2\] \[\displaystyle y = -\frac{b}{a}(x-k) + h = \frac{3}{4}(x-4) + 2\]Graficamente:
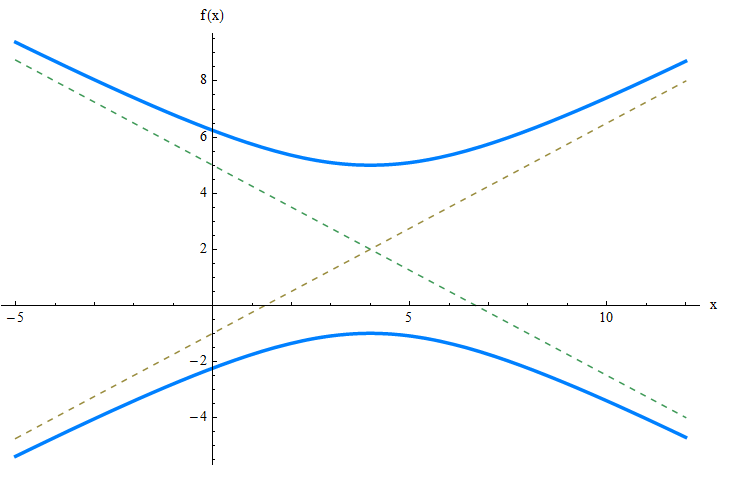
ESEMPIO 2
Trova l'equazione dell'iperbole con fuochi a \((-4, 0)\) e \((4, 0)\) vertice, concentrati su \((6, 0\).
RISPOSTA:
Si noti che i fuochi e i vertici sono sull'asse x, quindi l'iperbole si apre lungo l'asse x. Inoltre, poiché i fuochi sono simmetrici rispetto all'origine, e un vertice è \((4, 0)\), otteniamo \(a = 4\). E poiché un focus è su \((6, 0)\), otteniamo quel \(b = \sqrt{6^2 - 4^2} = \sqrt{20} = 2\sqrt 5\).
Pertanto, l'equazione dell'iperbole è:
\[\large \displaystyle \frac{(y-h)^2}{b^2} - \frac{(x-k)^2}{a^2} = 1 \] \[\large \displaystyle \Rightarrow \frac{x^2}{16} - \frac{y^2}{20} = 1 \]L'iperbole e le sezioni coniche generali
Come nel caso della parabola, l'iperbole è strettamente correlata al cono. Infatti un matematico greco di nome Apollonio è quello che ha scoperto questa connessione, comprendendo il concetto di sezioni coniche.
Una sezione conica si verifica quando si esegue un taglio di un cono con un piano e, a seconda dell'angolo relativo del cono e del piano nel punto di taglio, il cono viene tagliato in modo che la sezione trasversale abbia una forma specifica .
Quindi, a seconda dell'angolo di taglio relativo, abbiamo diverse forme della sezione, e queste sono la parabola, il cerchio, l'ellisse e l'iperbole. Vedi il grafico sotto:
Altro sull'iperbole
Un'iperbole con vertice all'origine, che si apre lungo l'asse x ha l'equazione \(\displaystyle \frac{x^2}{a^2} - \frac{y^2}{a^2} = 1 \), mentre un'iperbole, che si apre lungo l'asse y ha l'equazione \(\displaystyle \frac{y^2}{a^2} - \frac{x^2}{a^2} = 1 \).
Quindi, un vertice generale può essere ottenuto semplicemente applicando una traduzione a un dato punto \((k, h)\).
Applicazioni
L'iperbole ha molte applicazioni nel mondo pratico, così come nell'astronomia. Una differenza con la parabola è che l'iperbole ha asintoti obliqui, che la parabola non ha.
Algebricamente parlando, un'iperbole assomiglia a un'ellisse molto più di una parabola, sebbene la differenza di segno con l'ellisse faccia un mondo di differenza nella sua forma e proprietà.
Un altro tipo importante di sezione conica è la parabola, di cui puoi imparare in questo tutorial . Inoltre, puoi anche imparare tutto quello che c'è da fare conoscere il cerchio e l'ellisse .