Imparare a fattorizzare è una delle abilità più cruciali che puoi apprendere. Il factoring ha così tante applicazioni, che sarai felice di dedicare del tempo per imparare tutto quello che c'è su di esso.

Un rapido ristoro sulla proprietà commutativa, associativa e distributiva. Per i numeri reali \(x\), \(y\) e \(z\), abbiamo le seguenti proprietà

(Associatività dell'addizione) \((x+y)+z = x+(y+z)\)

Commutatività dell'addizione) \( x + y = y + x\)

(Proprietà distributiva) \( x \cdot (y+z) = x \cdot y + x \cdot z\)

dove \(+\) e \(\cdot\) sono rispettivamente la somma e il prodotto di numeri reali.

Perché è utile sapere come fattorizzare?

Ci sono molte ragioni, ma una di quelle cruciali è che la fattorizzazione ci offre un modo semplice per risolvere le equazioni. In effetti, il factoring è IL modo in cui dobbiamo risolvere le equazioni.

Ad esempio, considera l'equazione in cui stiamo cercando di risolvere per \(x\):

Come facciamo a tal proposito? Bene, possiamo usare la proprietà distributiva per ottenere:

Pertanto, con quest'ultima espressione \( x(y+z) = 0\) abbiamo un esempio di factoring. Infatti, abbiamo preso l'espressione iniziale, \(xy+xz\) e l'abbiamo scomposta in \( x(y+z)\).

Quindi, ora dobbiamo risolvere un'equazione più semplice, che è \( x(y+z) = 0\). Perché è più facile? È perché ora che sappiamo che il prodotto \( x(y+z)\) è uguale a zero, allora uno dei fattori DEVE essere uguale a zero.

Quindi, se sappiamo che \(y+z = \not 0\), allora sappiamo che abbiamo bisogno di \(x = 0\).

LEZIONE : Un vantaggio del factoring è la possibilità di scrivere un'equazione come moltiplicazione di fattori uguale a zero. Quindi, ALMENO UNO DEI FATTORI DEVE ESSERE ZERO.

Ad esempio, quando dobbiamo risolvere per \(x\) nella seguente equazione:

non ci rendiamo conto che stiamo effettivamente fattorizzando quando lo facciamo

quindi abbiamo ridotto la nostra equazione a un prodotto di fattori uguale a zero: \(8x = 0\). Poiché uno dei fattori \(8\) non è uguale a zero, l'unica soluzione possibile è \(x = 0\).

In altre parole : se sai come fattorizzare, probabilmente lo saprai come risolvere le equazioni .

Come fattorizzare i polinomi

L'equilibrio viene raggiunto con una classe di espressioni molto generale che possiamo, spesso, fattorizzare in modo molto sistematico. Quella classe è la classe dei polinomi. Ad esempio, l'espressione

è un polinomio di grado 2. O l'espressione sotto

è un polinomio di grado 3.

In generale, un'espressione della forma

è un polinomio di grado \(n\). Naturalmente, più semplice è l'espressione, più facile sarà semplificarla, quindi dovremmo prima provare a imparare a fattorizzare le espressioni quadratiche. Questo è, polinomi di secondo grado.

ESEMPIO 1

Fattorizzare la seguente espressione quadratica

RISPOSTA:

Questo esempio ti mostrerà, apposta, che può essere complicato considerare anche l'espressione più semplice, come quella sopra. Cosa faresti per tenerne conto?

E se ti dicessi, devi aggiungere zero? È abbastanza ridicolo, vero? Vediamo:

Sei d'accordo con quanto sopra? Ho appena aggiunto \(0\). Niente è cambiato. Ma se ti dicessi che \(0 = 2x - 2x\)? Allora

Lo stesso! Funziona, perché ho aggiunto zero, quindi non cambia nulla. Ma ora lo espandiamo e lo raggruppiamo:

Quindi, finalmente, \(x^2 + x - 2 = (x+2)(x-1)\). Difficile? Forse, ma questo è un modo per farlo. Nonostante sia un modo intelligente per farlo, preferiremmo un modo più sistematico.

Fattorizzare un polinomio quadratico

I trucchi intelligenti sono belli, e tutto il resto, ma di solito preferiremo un approccio sistematico, che non fallisce mai. Per i polinomi quadratici (polinomi di grado 2), esiste un modo sistematico di procedere con la fattorizzazione:

Passo 1 : Data l'espressione quadratica \(ax^2 + bx + c\), prima risolviamo l'equazione

Passo 2 : Se le soluzioni (radici) dell'equazione precedente sono reali (anche se esiste una sola radice), chiamiamo quelle radici \(x_1\) e \(x_2\). Con queste radici, otteniamo i seguenti fattori:

quindi le soluzioni \(x_1\) e \(x_2\) determinano completamente i fattori.

Naturalmente in questo caso, come previsto, la risoluzione di un'equazione quadratica è strettamente collegata alla fattorizzazione dell'equazione quadratica.

ESEMPIO 2

Fattorizzare la seguente equazione quadratica

calcolando le sue radici.

RISPOSTA:

Iniziamo risolvendo la corrispondente equazione quadratica:

usando il famoso e noto formula quadratica :

il che implica che le soluzioni (radici) sono \(x_1 = 1\) e \(x_2 = 1\). Quindi, l'espressione quadratica \(x^2 - 4x + 3\) può essere fattorizzata come segue:

Si noti che in questo caso il termine moltiplicando il termine \(x^2\) è 1, quindi in questo caso \(a = 1\).

Fattorizzazione di polinomi con grado maggiore di 2

Quindi, per fattorizzare i polinomi quadratici mi limito a calcolare le radici della corrispondente equazione quadratica. Come si fattorizzano i polinomi di grado superiore ?? Utilizzando esattamente lo stesso metodo .

Passo 1: Data l'espressione polinomiale \(a_n x^n + a_{n-1}x^{n-1} + ... + a_1 x + a_0\), prima risolviamo l'equazione

Passo 2: Se le soluzioni (radici) dell'equazione precedente sono reali (anche se vengono ripetute), chiamiamo quelle radici \(x_1\), \(x_2\), ..., \(x_n\). Con queste radici, otteniamo i seguenti fattori:

Quindi, sembrerebbe che sia altrettanto semplice fattorizzare un polinomio di grado 2 che fattorizzare un polinomio di grado 10. Teoricamente, la risposta è sì.

L'unico problema è che non esiste una formula algebrica semplice e ravvicinata che possa risolvere le radici per un'equazione polinomiale di grado 5 o superiore.

A volte, possiamo risolvere equazioni di grado superiore guardando il grafico o anche utilizzando la calcolatrice. Ad esempio, controlla il grafico seguente:

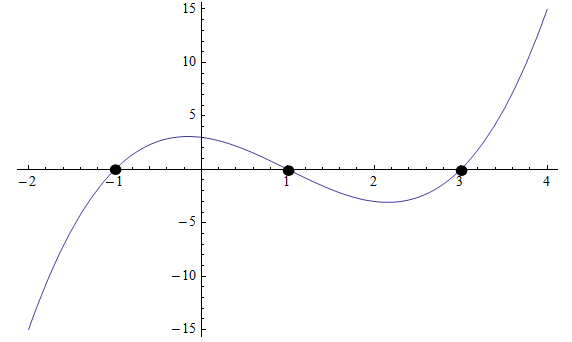
Graficamente, possiamo vedere che il polinomio attraversa l'asse x in tre punti: \(x_1 = -1\), \(x_2 = 1\) e \(x_3 = 3\), quindi queste sono le radici.

Quindi, sappiamo che il polinomio deve essere nella forma \(p(x) = a(x+1)(x-1)(x-3)\). Avremmo bisogno di conoscere un punto in più per conoscere la costante \(a\).