Risolvere le equazioni logaritmiche
La risoluzione delle equazioni logaritmiche è qualcosa che dovrai fare spesso quando si tratta di procedure algebriche e vale la pena di sviluppare una strategia concreta per affrontarle.
Quello che imparerai in questo tutorial è le principali strategie che devi seguire per risolvere le equazioni logaritmiche.
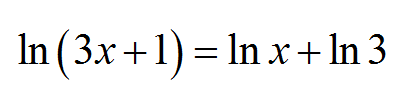
Qual è l'equazione logaritmica?
La prima cosa che dobbiamo definire quale sia un'equazione logaritmica.
Un'equazione logaritmica è un'equazione che comporta almeno una variabile sconosciuta, dove un'espressione logaritmica appare in almeno un lato dell'equazione
.
Un esempio di un'equazione logaritmica è
\[\ln x = 2\ln x - \ln 3\]o anche
\[ \ln(3x-1) - \ln(2x + 1) = 1\]
Si noti che un'equazione logaritmica può contenere più di uno sconosciuto, come ad esempio
Strategie per risolvere le equazioni logaritmiche
Il primo disclaimer è che non ci sono modi a prova di proiettile per risolvere un'equazione logaritmica, né un'equazione generale per quella materia.La ragione di ciò è tutti i metodi assumono una certa struttura nell'equazione, che non è necessariamente lì in tutte le equazioni.
Quindi, non possiamo trovare il modo di risolvere le equazioni logaritmiche, perché non c'è un modo in cui si occuperà di tutti i casi possibili.
Tuttavia, c'è un paio di strategie da seguire che ti darà la migliore possibilità di passare attraverso l'equazione e trovare una soluzione, se si esiste uno.
Innanzitutto, prova a raggruppare tutte le espressioni logaritmiche in un'espressione logaritmica.
Questo è ottenuto in genere utilizzando il più comune Regole del Registro , che ti consente di compattare un'espressione logaritmica, se la struttura dell'espressione lo consente così.
In secondo luogo, una volta che le espressioni logaritmiche sono compattate il più possibile, ti libererai di loro, applicando tipicamente la funzione esponenziale a entrambi i lati dell'uguaglianza.
Quest'ultimo passo, si spera, rimuoverà tutti i logaritmi dall'immagine, e ti consentirà di risolvere gli sconosciuti.
Quindi, in altre parole, risolvere un'equazione logaritmica consiste nel raggruppare le espressioni logaritmiche, eliminandoli applicando esponenziale e quindi risolvere l'equazione come un'equazione regolare.
Ovviamente, quando hai sbarazzato dei logaritmi, affronti un'equazione che potrebbe avere le sue sfide.
Risolvere diversi esempi di equazioni logaritmiche
Non esiste un modo migliore per imparare come risolvere le equazioni che effettivamente praticarle di risolverle:
ESEMPIO 1:
Risolvi la seguente equazione:
\[\large 4 \log(\sqrt x) = \log(6x-1)\]RISPONDERE:
Seguiamo le strategie.L'idea è di compattare il più possibile le espressioni logaritmiche.Questa è una chiamata di giudizio, perché l'idea principale è essenzialmente liberata dei logaritmi.
Usando le regole del registro, possiamo mettere il "4" all'interno del logaritmo come
\[\large 4 \log(\sqrt x) = \log(6x-1)\] \[\large \Rightarrow \log((\sqrt x)^4) = \log(6x-1)\] \[\large \Rightarrow \log(x^2) = \log(6x-1)\]Ora che le espressioni logaritmiche sono il più compatte possibile, dobbiamo sbarazzarci dei logaritmi.
Un modo per farlo è applicare la funzione esponenziale \(10^x\) a ciascun lato dell'uguaglianza.Cosa intendo con quello ???
Bene, hai due lati in quella uguaglianza.Poiché entrambe le parti sono le stesse, se utilizzate come argomenti della funzione \(10^x\), dovrebbe preservare l'uguaglianza.Così abbiamo
\[\large \log(x^2) = \log(6x-1)\] \[\large \Rightarrow 10^{\log(x^2)} = 10^{\log(6x-1)}\] \[\large \Rightarrow x^2 = 6x-1\]Perché sappiamo che \(10^{\log a} = a\), che è una delle regole di registro di base.
Quindi ora che abbiamo eliminato i logaritmi, possiamo risolvere l'equazione che è rimasta:
\[\large x^2 = 6x-1\] \[\large \Rightarrow x^2 - 6x + 1 = 0\] \[\large \Rightarrow x = \frac{-(-6) \pm \sqrt{(-6)^2-4(1)(1)}}{2(1)}\] \[\large \Rightarrow x = \frac{6 \pm \sqrt{36-4}}{2}\] \[\large \Rightarrow x = \frac{6 \pm \sqrt{32}}{2}\] \[\large \Rightarrow x = \frac{6 \pm 4\sqrt{2}}{2}\] \[\large \Rightarrow x = 3 \pm 2\sqrt 2\]Quindi \(x_1 = 3 + 2\sqrt 2\) e \(x_2 = 3 - 2\sqrt 2\).Tecnicamente, è necessario verificare se questi due sono soluzioni dell'equazione originale, quindi assicurarsi che appartengano al dominio delle espressioni logaritmiche.
In questo caso, entrambi \(x_1 = 3 + 2\sqrt 2\) e \(x_2 = 3 - 2\sqrt 2\) sono le soluzioni dell'equazione originale.
Esempio 2:
Risolvi la seguente equazione logaritmica:
\[\large \ln 5 - \ln(6-x) = \ln x\]RISPONDERE:
Usando le regole del registro, possiamo compattare le espressioni del registro, lo otteniamo
\[\large \ln 5 - \ln(6-x) = \ln x\] \[\large \displaystyle \Rightarrow \ln\left(\frac{5}{6-x}\right) = \ln x\] \[\large \displaystyle \Rightarrow e^{\ln\left(\frac{5}{6-x}\right)} = e^{\ln x}\] \[\large \displaystyle \Rightarrow \frac{5}{6-x} = x\]Perché sappiamo che \(e^{\ln a} = a\), che è una delle regole di registro di base.
Pertanto, ora che abbiamo eliminato i logaritmi, possiamo risolvere l'equazione che abbiamo lasciato:
\[\large \displaystyle \frac{5}{6-x} = x\] \[\large \displaystyle \Rightarrow 5 = x(6-x)\] \[\large \displaystyle \Rightarrow 5 = 6x - x^2\] \[\large \displaystyle \Rightarrow x^2 -6x + 5 = 0\] \[\large \displaystyle \Rightarrow (x-1)(x-5) = 0\]Quindi \(x_1 = 1\) e \(x_2 = 5\).Cerchiamo questi valori nell'equazione originale per vedere se sono in realtà soluzioni:
Per \(x_1 = 1\):
quale è lo stesso di:
\[\large \ln 5 - \ln(5) = 0\]Il che è vero, quindi l'equazione tiene.
Per \(x_1 = 5\):
quale è lo stesso di:
\[\large \ln 5 - \ln(1) = \ln(5)\]Il che è vero, quindi l'equazione tiene.
Pertanto, le soluzioni all'equazione sono \(x_1 = 1\) e \(x_2 = 5\).
Maggiori informazioni sulla risoluzione delle equazioni logaritmiche
Una cosa di cui gli studenti sono più preoccupati è come si libera di accedere un'equazione.Ma abbiamo visto che è in realtà la parte facile.Ciò che è più difficile è effettivamente lavorare algebricamente l'espressione in modo che i registri possano essere rimossi.
Ciò porta la questione su come affrontare basi diverse, che richiede il proprio paragrafo.
Risolvere equazioni logaritmiche con basi diverse
Negli esempi sopra riportati abbiamo affrontato solo \(\log\) (logaritmo con base 10) e \(\ln\) (logaritmo con base \(e\)).Come lo fai quando hai un logaritmo con una base diversa, come \(\log_a\) ???
La risposta è semplice: per eliminare i logaritmi con una base diversa, dire \(\log_a\) che ha base \(a\) che usiamo semplicemente la funzione esponenziale \(a^x\).Semplice giusto ??
Infatti, eliminando il logaritmo è la facile parte della risoluzione delle equazioni del registro.La parte più difficile del processo è di raggruppare e compattare le espressioni logaritmiche in un modulo che li elimini.
Puoi saperne di più su come funziona la funzione logaritmica vedendo Le proprietà del suo GRAFICO e studiando Regole del registro di base .