Ulteriori informazioni su questa calcolatrice di determinanti.

Nell'algebra lineare e nell'uso delle matrici, l'idea del determinante di una matrice \(A\) è un concetto di estrema importanza.

Questo perché il suo utilizzo è legato a quasi tutte le operazioni significative che si vogliono fare con le matrici, come la verifica dell'invertibilità delle matrici, trovare l'inversa di una matrice o sistemi risolutivi .

Quindi, ovunque si guardi quando si lavora con le matrici, si troveranno determinanti in un modo o nell'altro. È quindi molto importante acquisire familiarità con essi.

Come può aiutarvi questa calcolatrice a matrice

1. Tutto quello che dovete fare è digitare la vostra matrice
2. Deve essere una matrice quadrata, cioè una matrice con lo stesso numero di righe e colonne
3. Basta fare clic sul pulsante e la calcolatrice mostrerà tutti i passaggi e il valore finale del determinante
4. Il calcolo dei determinanti può essere estremamente laborioso e soggetto a errori. Questa calcolatrice vi risparmia questi problemi

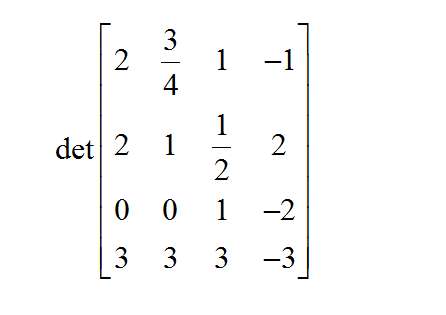
Come si calcola il determinante di una matrice?

La risposta potrebbe essere lunga, perché ci sono molti modi per calcolare il determinante di una matrice. Diciamo innanzitutto che il determinante si calcola solo per le matrici quadrate (cioè le matrici che hanno lo stesso numero di righe e colonne).

Quindi, la matrice più piccola per la quale possiamo calcolare un determinante è una matrice 2x2. Consideriamo una generica matrice 2x2, come mostrato di seguito:

\[ A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}\]

Qual è la formula del determinante? In questo caso, il determinante della matrice \(A\) si calcola semplicemente come \(\det(A) = a d - bc\)

Quindi, ad esempio, se avessimo:

\[ A = \begin{bmatrix} 1 & 2 \\ 1 & 3 \end{bmatrix}\]

il determinante della matrice \(A\) sarebbe \(\det(A) = 1 \cdot 3 - 2 \cdot 1 = 3 - 2 = 1\). Facile, no?

Come si trova il determinante di una matrice 3x3?

Ora, per le matrici più grandi, il calcolo del determinante si basa sul sottodeterminante di matrici più piccole. Per dare un'idea, vediamo un modo di calcolare il determinante di una matrice 3x3. Consideriamo

\[ A = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}\]

In questo caso, il determinante della matrice 3x3 \(A\) viene calcolato in base all'operazione di più determinanti 2x2

\[\det(A) = a \det \begin{bmatrix}e & f \\ h & i \end{bmatrix} - b \det \begin{bmatrix} d & f \\ g & i \end{bmatrix} + c \det\begin{bmatrix} d & e \\ g & h \end{bmatrix}\]

Nelle equazioni precedenti i valori \(a\), \(b\), \(c\) svolgono il ruolo di perni e possono avere segno negativo. Il segno di un perno è \((-1)^{i+j}\), dove il perno corrispondente si trova nella riga \(i\) e nella colonna \(j\).

Ad esempio, \(a\) è nella riga 1, colonna 1, quindi il suo segno è \((-1)^{1+1} = (-1)^2 = 1\) (positivo). Inoltre, \(b\) è nella riga 1, colonna 2, quindi il suo segno è \((-1)^{1+2} = (-1)^3 = -1\) (negativo), e così via.

La magia consiste nello scegliere qualsiasi riga o colonna come perno. Ogni perno avrà un segno associato (positivo o negativo) e un sottodeterminante, che sono correlati con il parametro cofattori della matrice .

Questo sottodeterminante è il determinante effettivo della matrice originale dopo aver rimosso la riga \(i\) e la colonna \(j\), per il perno che si trova nella riga \(i\) e nella colonna \(j\).

La convenzione più logica indica di scegliere la riga o la colonna con il maggior numero di zeri per i pivot, in modo da evitare di calcolare alcuni dei sottodeterminanti, se possibile.

Come si trova il determinante di una matrice 3x4?

Non è possibile farlo. Una matrice 3x4 non è una matrice quadrata e quindi non è possibile calcolare il determinante. Per calcolare un determinante, la matrice deve avere lo stesso numero di righe e colonne.

Calcolo del determinante 4x4

Per le matrici più grandi, la metodologia è la stessa: scegliere una riga o una colonna come perno, idealmente quella con il maggior numero di zeri. Trovare il segno corrispondente a ciascun perno e trovare i sottodeterminanti corrispondenti.

Quindi si riduce il calcolo del determinante di una matrice 4x4 all'operazione di quattro determinanti 3x3. E a sua volta, ciascuno dei determinanti 3x3 si trova come operazione di diversi determinanti 2x2, per i quali conosciamo una formula.

Quindi, la situazione può diventare molto complicata in breve tempo.

Esempio di calcolo del determinante di una matrice

Question: Si consideri la seguente matrice:

\[ \begin{bmatrix}1&2&3\\3&1&4\\2&3&8\end{bmatrix}\]

Calcolare il determinante della matrice data, mostrando i passaggi.

Soluzione: Dobbiamo calcolare il determinante della matrice \(3 \times 3\) che ci è stata fornita.

Utilizzando la formula del sottodeterminante si ottiene:

\[ \begin{vmatrix} \displaystyle 1&\displaystyle 2&\displaystyle 3\\[0.6em]\displaystyle 3&\displaystyle 1&\displaystyle 4\\[0.6em]\displaystyle 2&\displaystyle 3&\displaystyle 8 \end{vmatrix} = 1 \cdot \left( 1 \cdot \left( 8 \right) - 3 \cdot \left(4 \right) \right) - 2 \cdot \left( 3 \cdot \left( 8 \right) - 2 \cdot \left(4 \right) \right) + 3 \cdot \left( 3 \cdot \left( 3 \right) - 2 \cdot \left(1 \right) \right)\] \[ = 1 \cdot \left( -4 \right) - 2 \cdot \left( 16 \right) + 3 \cdot \left( 7 \right) = -15\]

Conclusione : In base ai calcoli illustrati sopra, si scopre che il determinante della matrice è \(\det A = \displaystyle -15\).

Altre utili calcolatrici di matrici che si possono utilizzare

I calcoli delle matrici eseguiti a mano richiedono molto lavoro, quindi potete sfruttare i nostri risolutori di algebra lineare.

In primo luogo, è possibile utilizzare questa calcolatrice di matrici inverse per calcolare l'inverso di una matrice mostrando i passaggi, e lo si può fare sia con metodo adjoint o utilizzando Riduzione RREF .