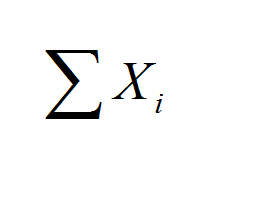Calcolatore di somma
Istruzioni: Usa questo calcolatore di somma per calcolare qualsiasi espressione valida che coinvolga le somme fornite, mostrando tutti i passaggi. Si prega di digitare il calcolo della frazione che si desidera eseguire nella casella del modulo sottostante.
Maggiori informazioni su questo calcolatore di somma
Questa calcolatrice ti permetterà di calcolare e semplificare le espressioni che coinvolgono le somme degli oggetti Algebra più comuni, come numeri, frazioni, radicali e funzioni comuni, mostrando tutti i passaggi. È necessario fornire un'espressione valida che comporti somme/addizioni. Ad esempio, potrebbe essere qualcosa di semplice come '3/4 + 1/3', o qualcosa di più complesso come 'sqrt(1/3+1/4)+(1/8+1/6)'.
Una volta fornita un'espressione numerica valida, basta cliccare su "Calcola", e il nostro calcolatore ti mostrerà tutti i passaggi.
Fare somme di termini di algebra di base può sembrare semplice, ed è abbastanza semplice, diventa solo laborioso e soggetto a errori quando devi lavorare su un termine lungo e contorto.

Come aggiungere espressioni?
Aggiungere insieme espressioni più semplici è semplice e hai due potenti strumenti a tua disposizione: le regole di associatività e commutatività .
In parole povere, l'associatività dice che quando si aggiungono termini, le parentesi possono essere rimosse in modo sicuro e il risultato non cambierà. Inoltre, commutatività significa che puoi cambiare l'ordine di una somma e il risultato non cambierà.
Quali sono i passaggi per aggiungere un'espressione?
- Passaggio 1: identificare l'espressione che si desidera semplificare e identificare la parte che consiste solo di somme e può essere isolata
- Passaggio 2: utilizzando la regola associativa, puoi rimuovere le parentesi ovunque siano coinvolte solo le somme
- Passaggio 3: esegui l'aggiunta termine per termine e puoi cambiare l'ordine degli operandi, se utile
- Passaggio 4: le regole sopra si applicano anche alle espressioni che consistono solo in moltiplicazioni, ma non necessariamente quando le mescoli
Queste regole non funzionano con sottrazioni o divisioni. Cioè, quando hai sottrazioni non puoi semplicemente rimuovere le parentesi, perché il risultato può davvero cambiare. Infatti, ad esempio se hai \(1-(3-1)\) che è correttamente semplificato come \(1-(3-1) = 1 - 2 = -1 \), che non è lo stesso di quello che ottieni rimuovendo semplicemente le parentesi: \(1-3-1\) che semplifica a -3, quindi il risultato cambia.
Come aggiungere espressioni?
L'idea è quella di raggruppare termini simili: tra i termini che stai aggiungendo, puoi raggruppare numeri, frazioni e quindi utilizzarli.
L'idea è di utilizzare termini che possono essere facilmente gestiti insieme, come numeri e frazioni. Quindi, se hai un'espressione più complessa e composta, lavori dall'interno verso l'esterno, ma osservando prima le operazioni facili.
La cura principale che devi prestare è quando hai le parentesi, notando che non possono essere semplicemente rimosse se hai un mix di operazioni. La proprietà associativa funziona solo quando non vi è alcuna combinazione di diverse operazioni.
Perché è utile aggiungere espressioni?
L'aggiunta di espressioni semplici è una delle operazioni più basilari che puoi eseguire ed è una pietra miliare in qualsiasi operazione matematica, punto.
È davvero impossibile sopravvalutare l'importanza di aggiungere correttamente e correttamente le frazioni espressioni semplificative raggruppando e utilizzando l'ordine di operazione corretto.

Esempio: calcolo della somma delle espressioni
Calcola quanto segue: \(\frac{1}{3} + \left(\frac{6}{4} - \frac{5}{6}\right)\)
Soluzione: Dobbiamo calcolare e semplificare la seguente espressione: \(\displaystyle \frac{1}{3}+\left(\frac{6}{4}-\frac{5}{6}\right)\).
Si ottiene il seguente calcolo:
Esempio: calcolo della somma dell'espressione
Calcola quanto segue: \(2 + \frac{5}{4} - \frac{7}{6}\)
Soluzione: Dobbiamo calcolare e semplificare la seguente espressione: \(\displaystyle 2+\frac{5}{4}-\frac{7}{6}\).
Si ottiene il seguente calcolo:
che conclude il calcolo.
Esempio: un altro calcolo di addizione
Calcola \( \left(\frac{4}{3} \times \frac{6}{5} \right)+ \frac{1}{5} \).
Soluzione: Dobbiamo calcolare e semplificare la seguente espressione: \(\displaystyle \left(\frac{4}{3}\cdot\frac{6}{5}\right)+\frac{1}{5}\).
Si ottiene il seguente calcolo:
che conclude il calcolo.
Altri utili calcolatori di algebra
Le aggiunte sono le operazioni più fondamentali che puoi eseguire. Puoi anche usare a Calcolatrice di frazioni per fare addizioni di frazioni in particolare.
Inoltre, quando si lavora con le frazioni c'è un caso speciale che tratta termini come '1 1/2', per il quale puoi usare un calcolatore di frazioni miste