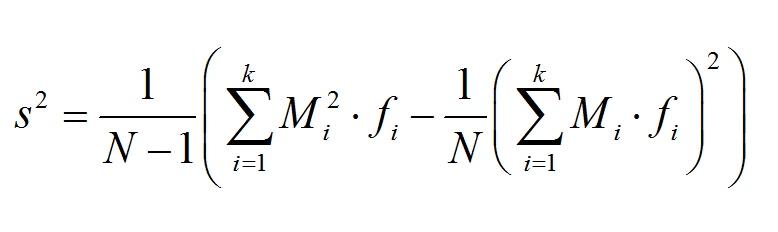Calcolatore di analisi della varianza unidirezionale

Per saperne di più sul Test ANOVA a una via così puoi capire meglio i risultati forniti da questo risolutore. Prima di tutto, ANOVA o Analisi delle varianze è uno dei campi più importanti della statistica. La ragione di ciò è che va al centro dell'analisi dei campioni di variazione esibiti, suddividendo la variazione totale in varie diverse fonti di variazione.

L'uso più basilare di ANOVA è testare la differenza tra le popolazioni per diversi gruppi (2 o più). Ricordiamo che un test t viene utilizzato per confrontare le medie di due gruppi, quindi ANOVA è un'estensione di tipo che consente di eseguire confronti per due o più gruppi.

Come con qualsiasi altro test di ipotesi, ANOVA utilizza un'ipotesi nulla e alternativa. L'ipotesi nulla è un'affermazione che afferma che tutte le medie della popolazione sono uguali, e l'ipotesi alternativa è l'ipotesi che non tutte le medie sono uguali (osserva che questo NON implica che tutte le medie siano disuguali, implica che almeno una coppia di medie è disuguale).

Come si calcola un anova?

L'esecuzione di un test ANOVA è un po' come l'esecuzione di qualsiasi altro test parametrico e sarà quindi necessario soddisfare alcuni presupposti. Le principali ipotesi richieste per eseguire un'ANOVA unidirezionale sono:

• La variabile dipendente (DV) deve essere misurata almeno a livello di intervallo


• I gruppi devono provenire da popolazioni normalmente distribuite


• I gruppi devono provenire da popolazioni normali con varianze di popolazione uguali

Se i risultati dell'ANOVA sono significativi, ovvero l'ipotesi nulla viene rifiutata, possiamo eseguire a Test post-hoc per valutare esattamente quali coppie differiscono in modo significativo. Esempi di test post-hoc sono l'LSD di Fisher, il test di Tukey, la correzione di Bonferroni, ecc.

Le ipotesi nulle di un test ANOVA vengono respinte quando il Statistiche F supera il valore del rapporto F critico che viene calcolato, in base ai corrispondenti gradi di libertà.

Quando hai k gruppi e una dimensione totale del campione di N, allora i gradi di libertà del numeratore sono dfN = k - 1, e i gradi di libertà del denominatore sono dfD = N - k - 2.

Quando alcuni dei presupposti non sono soddisfatti (in particolare il secondo è il terzo), ci sono opzioni correttive per alcune statistiche più robuste. Quando ci sono gravi violazioni delle ipotesi, sarebbe più appropriato utilizzare un'alternativa non parametrica, come il test di Kruskal-Wallis.

Questo calcolatore ANOVA con passaggi fornisce informazioni sufficienti per rifiutare o non rifiutare l'ipotesi nulla, in base al rapporto F calcolato. Se viene calcolata l'ipotesi nulla, sarà necessario eseguire un test post-hoc.

Perché invece non viene utilizzato un t-test

Due test T campione indipendenti sono progettati per condurre un confronto tra due gruppi. Quando hai più di due gruppi, l'unico modo per confrontare è condurre diversi confronti a coppie.

Ciascuno di questi confronti a coppie ha una certa probabilità di un errore di tipo I, quindi l'errore di tipo I per famiglia è la probabilità che almeno uno di questi confronti porti a un errore di tipo I. Quando vengono eseguiti molti confronti, la probabilità familiare di un errore di tipo I viene notevolmente gonfiata

Un'ANOVA unidirezionale è progettata per confrontare due o più medie campionarie, ma se si desidera confrontare due medie campionarie, potrebbe essere più efficiente utilizzare direttamente la nostra t-test per due campioni indipendenti .

Alternative non parametriche all'anova

L'ANOVA richiede che siano valide determinate ipotesi, vale a dire la normalità e l'omogeneità delle varianze. È noto che ANOVA è relativamente robusto alla violazione delle ipotesi, specialmente se sono lievi. Ma cosa fare quando le ipotesi semplicemente non sono soddisfatte?

In tal caso puoi utilizzare il nostro Calcolatrice del test di Kruskal-Wallis , che è l'equivalente non parametrico di ANOVA. Un vantaggio del test Kruskal-Wallis è che puoi usarlo anche con dati ordinali, per i quali l'uso di ANOVA non sarebbe una buona idea.