Règle de Cramer
La règle de Cramer est une technique utilisée pour résoudre systématiquement des systèmes d'équations linéaires, basés sur les calculs de déterminants.
En règle générale, résoudre systèmes d'équations linéaires peut être compliqué pour les systèmes dont la taille est supérieure à 2x2, car il existe de nombreuses façons de le réduire lorsqu'il y a trois variables ou plus.
La règle de Cramer fournit un moyen sans équivoque et systématique de trouver des solutions aux systèmes d'équations linéaires, quelle que soit la taille du système.
Le nombre de calculs requis augmente pour les grands systèmes, mais la procédure est exactement la même, quelle que soit la taille du système.
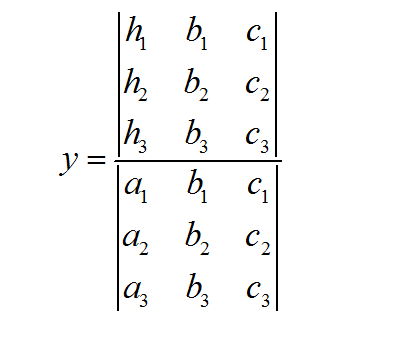
Comment utiliser la règle de Cramer
Afin de faciliter les choses, nous travaillerons sur le cas de \(n = 2\) et ensuite nous établirons une version plus générale qui, espérons-le, aura plus de sens après avoir abordé le cas \(n=2\).
Étape 1
: Tous les systèmes linéaires 2x2 peuvent être écrits sous la forme suivante:
Donc, votre première étape consiste à trouver ces valeurs \(a_1, b_1, c_1\) et \(a_2, b_2, c_2\) pour le système que vous souhaitez résoudre.
Étape 2
: Une fois que vous avez les coefficients \(a_1, b_1, c_1\) et \(a_2, b_2, c_2\), vous utilisez les formules suivantes pour résoudre \(x\) et \(y\):
Dans la formule ci-dessus, où il dit "det", cela signifie le déterminant de la matrice correspondante. Parfois, une notation plus compacte est utilisée pour les déterminants, comme indiqué ci-dessous:
\[\large \displaystyle \det \left[\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right] = \left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right| \]Donc, en utilisant la notation ci-dessus, nous obtiendrions ces formules plus compactes pour la règle de Cramer:
\[\large \displaystyle x = \frac{ \left|\begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \] \[\large \displaystyle y = \frac{ \left|\begin{matrix} a_1 & c_1 \\ a_2 & c_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \]Ayons une manière visuelle de comprendre ce qui se passe. Observez que \(x\) et \(y\) ont le même déterminant dans le dénominateur.
Les coefficients de cette matrice commune utilisée dans le dénominateur sont directement dérivés des coefficients qui multiplient \(x\) et \(y\) dans le système. Voir l'image ci-dessous:
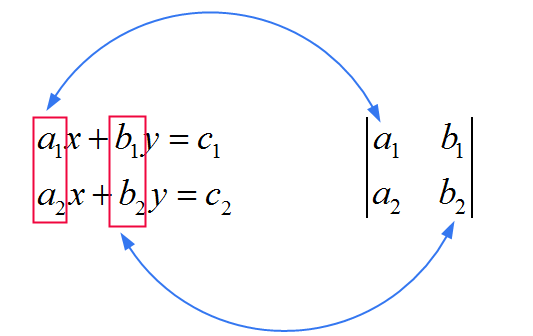
Maintenant, nous voyons que \(x\) et \(y\) diffèrent par ce qu'ils ont dans le numérateur. Pour vous souvenir de la règle, pensez à ceci:
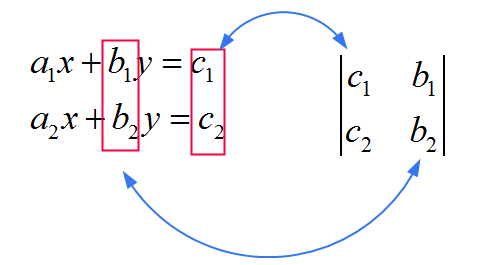
Pour \(x\), vous utilisez la même matrice que celle du dénominateur, mais vous remplacez la PREMIÈRE colonne par les coefficients \(c_1\) et \(c_2\). Voir l'image ci-dessous
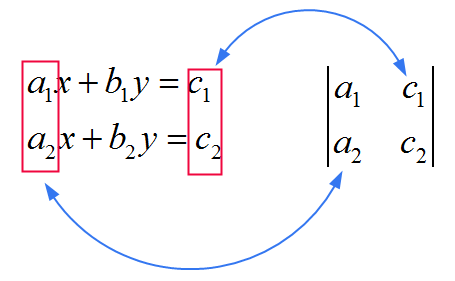
Pour \(y\), vous utilisez la même matrice que celle du dénominateur, mais vous remplacez la SECONDE colonne par les coefficients \(c_1\) et \(c_2\). Voir l'image ci-dessous
EXEMPLE 1
Résolvez le système linéaire 2x2 suivant:
\[\large 2x + 8y = 10\] \[\large 2x - 4y = 4\]RÉPONDRE:
Suivons les deux étapes que nous avons décrites ci-dessus pour utiliser la règle de Cramer pour résoudre le système ci-dessus:
Étape 1
: Nous devons identifier les coefficients des déterminants correspondants.
Pour la matrice qui entre dans le dénominateur, nous utilisons
\[ \left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right| = \left|\begin{matrix} 2 & 8 \\ 2 & -4 \end{matrix}\right| \]Maintenant, dans ce cas \(c_1 = 10, c_2 = 4\), pour le déterminant utilisé pour calculer \(x\), nous remplaçons la matrice précédente en changeant la PREMIÈRE colonne:
\[ \left|\begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}\right| = \left|\begin{matrix} 10 & 8 \\ 4 & -4 \end{matrix}\right| \]Pour le déterminant utilisé pour calculer \(y\) nous remplaçons la matrice précédente en changeant la SECONDE colonne:
\[ \left|\begin{matrix} a_1 & c_1 \\ a_2 & c_2 \end{matrix}\right| = \left|\begin{matrix} 2 & 10 \\ 2 & 4 \end{matrix}\right| \]Alors maintenant, nous avons la solution:
\[\large \displaystyle x = \frac{ \left|\begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \] \[ = \frac{\left|\begin{matrix} 10 & 8 \\ 4 & -4 \end{matrix}\right|}{\left|\begin{matrix} 2 & 8 \\ 2 & -4 \end{matrix}\right|} = \frac{10 \times (-4) - 4\times 8}{2 \times (-4) - 2 \times 8} = \frac{-72}{-24} = 3 \]et pour \(y\):
\[\large \displaystyle y = \frac{ \left|\begin{matrix} a_1 & c_1 \\ a_2 & c_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \] \[ = \frac{\left|\begin{matrix} 2 & 10 \\ 2 & 4 \end{matrix}\right|}{\left|\begin{matrix} 2 & 8 \\ 2 & -4 \end{matrix}\right|} = \frac{2 \times 4 - 2\times 10}{2 \times (-4) - 2 \times 8} = \frac{-12}{-24} = \frac{1}{2} \]Par conséquent, la solution est \(x = 3\), \(y = 1/2\).
Règle de Cramer pour le cas général
La beauté de la règle de Cramer est qu'elle applique exactement la même procédure, qu'il s'agisse d'un système 2x2 ou d'un système 10x10. Le concept est le même.
Donc, supposons que \(x_1, x_2, ..., x_n\) sont les variables (les inconnues), et nous voulons résoudre le système n x n d'équations linéaires suivant:
\[\large a_{11} x_1 + a_{12} x_2 + .... + a_{1n} x_n = c_1 \] \[\large a_{21} x_1 + a_{22} x_2 + .... + a_{2n} x_n = c_2 \] \[\large \vdots \] \[\large a_{n1} x_1 + a_{n2} x_2 + .... + a_{nn} x_n = c_n \]Afin de résoudre \(x_1, x_2, ..., x_n\), nous utiliserons le déterminant suivant sur le dénominateur:
\[\large\displaystyle \left|\begin{matrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & a_{nn}\end{matrix}\right|\]• La solution pour \(x_1\) est
\[\large\displaystyle x_1 = \frac{ \left|\begin{matrix} c_1 & a_{12} & ... & a_{1n} \\ c_2 & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ c_n & a_{n2} & ... & a_{nn}\end{matrix}\right| }{\left|\begin{matrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & a_{nn}\end{matrix}\right|} \]• La solution pour \(x_2\) est
\[\large\displaystyle x_1 = \frac{ \left|\begin{matrix} a_{11} & c_1 & ... & a_{1n} \\ a_{21} & c_2 & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & c_n \end{matrix}\right| }{\left|\begin{matrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & a_{nn}\end{matrix}\right|} \]Etc. Comme vous pouvez le voir, le déterminant dans le dénominateur est le même, et celui dans le numérateur est obtenu en changeant la première colonne avec \((c_1, ..., c_n)\) pour \(x_1\). Pour \(x_2\) nous changeons la deuxième colonne par \((c_1, ..., c_n)\), pour \(x_3\) nous changeons la troisième colonne, et ainsi de suite. Vous avez eu l'idée.
EXEMPLE 2
Résolvez le système suivant d'équations linéaires 3x3 en utilisant la règle de Cramer.
\[\large x_1 + x_2 + x3 = 20\] \[\large x_1 - x_2 + x3 = 4\] \[\large 2x_1 + x_2 - x3 = 16\]RÉPONDRE:
Tout d'abord, nous identifions le déterminant qui entre dans le dénominateur:
\[\large\displaystyle \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right|\]Aussi, nous devons identifier le vecteur des coefficients \(c_i\):
\[\large\displaystyle \left[\begin{matrix} 20 \\ 4 \\ 16 \end{matrix}\right]\]Ce vecteur sera celui qui remplacera les colonnes correspondantes du déterminant commun du dénominateur. On a:
\[\large\displaystyle x_1 = \frac{ \left|\begin{matrix} 20 & 1 & 1 \\ 4 & -1 & 1 \\ 16 & 1 & -1 \end{matrix}\right| }{ \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right| } = \frac{40}{6} = \frac{20}{3}\] \[\large\displaystyle x_2 = \frac{ \left|\begin{matrix} 1 & 20 & 1 \\ 1 & 4 & 1 \\ 2 & 16 & -1 \end{matrix}\right| }{ \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right| } = \frac{40}{6} = \frac{20}{3}\] \[\large\displaystyle x_3 = \frac{ \left|\begin{matrix} 1 & 1 & 20 \\ 1 & -1 & 4 \\ 2 & 1 & 16 \end{matrix}\right| }{ \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right| } = \frac{40}{6} = \frac{20}{3}\]En savoir plus sur la règle de Cramer
La règle de Cramer a un rôle spécifique dans la résolution efficace de systèmes d'équations linéaires. Cela implique l'utilisation de déterminants pour rendre très simple une tâche qui autrement serait vraiment compliquée, en particulier pour les systèmes plus grands.
En fin de compte, afin de solution des systèmes linéaires , tout ce que vous avez à faire est d'identifier une matrice de nombres déterminants en fonction du système à résoudre, et de mener une opération algébrique simple pour résoudre le système.
Applications
La règle de Cramer a de nombreuses applications à la fois dans l'algèbre linéaire et les équations différentielles.