Quelle est la racine carrée de 64?
Parfois, une simple question comme quelle est la racine carrée de 64 a une réponse qui peut confondre quelques-uns.Dans ce cas, nous dissiperons quelques mythes.
L'objectif principal de ce didacticiel est d'apprendre quelques éléments sur les racines carrées et les radicaux, afin que vous puissiez répondre à des questions à ce sujet sans hésitation.
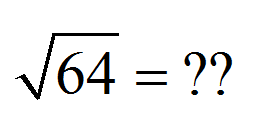
La première chose est la première.Épelons la définition de la racine carrée:
La racine carrée d'un nombre donné est la positive nombre (ou zéro) de sorte que, lorsque car au carré entraîne ce nombre donné .
C'est ça.Donc, donné un numéro \(x\), sa racine carrée est un nombre \(b\) de sorte que \(b \ge 0\) et
\[b^2 = x\]En regardant l'expression ci-dessus, nous pouvons voir que si \(b\) va être la racine carrée de \(x\), puis \(x = b^2\), et puisqu'un numéro carré ne peut pas être négatif, \(x\) ne peut être non négatif que (si nous voulons pouvoir être capable detrouver sa racine carrée).
Conclusion : Nous ne pouvons que calculer des racines carrées de valeurs non négatives \(x\).Ou dit différemment, le Domaine de la Fonction \(\sqrt x\) est \([0,+\infty)\).
Alors, répondant à notre question initiale:
Quelle est la racine carrée de 64?
Sur la base de ce que nous avons défini, nous devons trouver une valeur non négative \(b\) afin que \(b^2 = 64\).N'importe quel numéro répondant à ces propriétés viennent à l'esprit?
Eh bien, oui, et si nous essayions avec \(b = 8\)?Ok, alors \(b = 8\) est non négatif et \(b^2 = 8^2 = 64\).
Alors, nous avons trouvé la racine carrée de 64, ce qui est 8, car 8 n'est pas négatif et \(8^2 = 64\).Nous écrivons cela comme suit:
\[ \sqrt{64} = 8 \]Le mythe sur la fonction racine carrée
Maintenant, nous allons au sujet qui a motivé ce tutoriel ... La définition ci-dessus donnée de la racine carrée nous permet de jeter l'énoncé commun que "la racine carrée de 64 est plus ou moins 8", ce qui est faux.En effet
\[\sqrt{64} =\not \pm 8\]Maintenant, nous pouvons comprendre pourquoi un tel mythe continue.En effet, 8 et -8 ont la propriété que \(8^2 = 64\) et \((-8)^2 = 64\).Alors, pourquoi -8 n'est-il pas la racine carrée de 64?
Parce que par définition, nous avons dit que la racine carrée doit être ce nombre non négatif qui a la propriété qui, lorsqu'il est carré, ils sont égaux au nombre donné.Et -8 échoue la condition d'être non négatif.
Le graphique de la fonction racine carrée
Regardez le graphique de la fonction racine carrée ci-dessous:
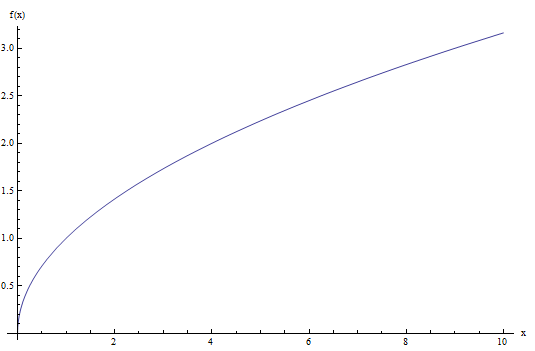
Comme vous pouvez le constater, cette fonction ne prend que des valeurs non négatives, et elle passe en réalité le test de ligne verticale, il s'agit donc d'une fonction.
Donc, à la fin, la définition de la racine carrée comme non négatif \(b\) de sorte que \(b^2 = x\) rend la racine carrée une fonction.
Si en effet, nous avions que \(\sqrt{64} = \pm 8\), alors \(\sqrt x\) ne serait pas une fonction, serait une relation à la place, car la ligne verticale à \(x = 64\) traverserait le graphique deux fois (8 et -8).
Qu'en est-il des autres fonctions radicales?
Il existe d'autres types de fonctions radicales.Par exemple, la racine cubique \(\sqrt[3] x\).Dans ce cas, il n'est pas nécessaire de faire une règle pour quel radical choisir, car la racine cubique d'un nombre donné \(x\) est le nombre \(b\) afin que \(b^3 = x\).
Racine cubique
Pour le cas de racine cubique, il n'est pas nécessaire de faire des distinctions car pour un \(x\) donné qu'il n'y aura qu'un numéro \(b\) tel que \(b^3 = x\).
Par exemple
\[\sqrt[3]{64} = 4\]simplement parce que \(4^3 = 64\).Ou
\[\sqrt[3]{-64} = -4\]simplement parce que \((-4)^3 = -64\).C'est, il n'y a pas d'ambiguïté comme dans le cas de la racine carrée.
Racine quartique
Pour le boîtier de racine quartique, il est similaire à la racine carrée.Nous aurons que \(\sqrt[4] x = b\) si \(b \ge 0\) et \(b^4 = x\).
Par exemple
\[\sqrt[4]{16} = 2\]Parce que \(2^4 = 16\) et \(2 \ge 0\).Mais
\[\sqrt[4]{16} =\not -2\]Parce que bien que \((-2)^4 = -16\), nous avons ce \(-2 < 0\) alors la condition de non-négativité n'est pas remplie.
Que diriez-vous de la n-ème racine \(\sqrt[n] x\) en général ???.
Je suis sûr que vous l'avez deviné.
Pour \(n\) Même, la situation est comme la racine carrée: \(\sqrt[n] x = b\) si \(b \ge 0\) et \(b^n = x\).
Pour \(n\) impair, la situation est comme la racine carrée: \(\sqrt[n] x = b\) si \(b^n = x\).
Plus sur le calcul de la racine carrée
Une chose que nous avons accentuée sur la fonction racine carrée \(\sqrt x\) doit prendre un argument non négatif \(x\) si nous voulions pouvoir calculer la racine carrée.
Nous avons triché un peu, car nous n'avons pas écrit la phrase complète: la fonction racine carrée \(\sqrt x\) doit prendre un argument non négatif \(x\) si nous voulions pouvoir calculer la racine carrée dans la ligne réelle.
Mais, si \(x < 0\), ceci est, si \(x\) est négatif, alors \(\sqrt x\) est toujours défini, mais pas comme un nombre réel mais comme un nombre complexe.
L'unité de base de la racine carrée complexe est la racine carrée de -1.Qu'est-ce que \(\sqrt{-1}\) ???
Entrez les numéros complexes: il y a un nombre complexe, appelé \(i\) afin que
\[\sqrt{-1} = i \]À partir de ce point, les propriétés de la racine carrée fonctionnent de la même manière.Par exemple:
\[\sqrt{-4} = \sqrt{4} \sqrt{-1} = 2\sqrt{-1} = 2i \]