Equations littérales
Les équations littérales sont des équations dans lesquelles il y a des symboles qui ne sont pas des variables, mais qui représentent une constante. C'est donc comme une équation, mais certains des nombres au lieu d'être des nombres sont exprimés sous forme de constantes génériques.
Dans ce didacticiel, vous apprendrez à gérer les équations littérales et à les utiliser.
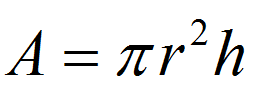
Qu'est-ce qu'une équation littérale
La première tâche à accomplir est de spécifier ce qu'est une équation littérale. Lorsque nous disons «littéral», nous parlons de «lettres». Oui, du latin littéral vient de «lettres»
Ainsi, une équation littérale est une équation qui implique beaucoup de «lettres», par opposition à des nombres. Ces lettres ne sont pas censées être des variables, elles sont censées représenter des nombres, en termes de constante générique.
Par conséquent, pour identifier une équation littérale, nous devons voir beaucoup de lettres, dont une (ou potentiellement plus) est la
variable
.
Comme dans toute autre équation, l'idée est de résoudre pour la variable (ce qui signifie isoler la variable d'un côté de l'équation).
Par exemple, considérons la formule du volume d'un cylindre de rayon \(r\) et de hauteur \(h\):
\[V = \pi r^2 h\]C'est une équation littérale. Pourquoi? Parce que nous avons une équation avec de nombreuses lettres.
La question est de savoir quelle est la variable et quelles sont les constantes. En vérité, c'est subjectif, dans une certaine mesure.
Par exemple, on pourrait affirmer que \(V\) est la variable et \(r\) et \(h\) sont les littéraux (ou constantes), et cela aurait du sens.
Mais on pourrait dire que par exemple, on nous donne le volume \(V\) et la hauteur \(h\), et vous devez trouver le rayon \(r\). Dans ce cas, nous avons la même équation littérale, mais la variable serait \(r\).
Il est pertinent de savoir quelle est la variable dans une équation littérale, afin de savoir ce que nous résolvons.
Stratégies pour traiter une équation littérale
Donc, nous avons une équation littérale, et maintenant? Eh bien, comme toute autre équation, nous devrions essayer de la résoudre.
Cela signifie que nous devons isoler la variable d'un côté de l'équation et mettre tout le reste, en utilisant toutes les règles algébriques disponibles, de l'autre côté.
Cela signifie, en termes pratiques, que nous exprimons la variable en termes (ou en fonction) des constantes (littéraux).
Le processus de résolution d'équations littérales est le même que celui de résolution d'équations régulières:
Nous ajoutons, soustrayons, multiplions ou divisons des termes des deux côtés de l'égalité afin d'isoler la variable.
Il n'y a pas une seule façon de faire la résolution, cela dépend des caractéristiques et de la structure de l'équation.
Exemples de résolution d'équations littérales
Le moyen le plus rapide d'apprendre une compétence en mathématiques est de PRATIQUER. Et c'est parti.
EXEMPLE 1:
Revenons à l'exemple du cylindre. Pour un cylindre de volume \(V\) et de hauteur \(h\) donnés, trouvez son rayon \(r\)
RÉPONDRE:
Nous savons que la formule du volume d'un cylindre est
\[\large V = \pi r^2 h\]Pour l'équation littérale ci-dessus, nous avons que la variable (celle que nous voulons résoudre) est \(r\) et les constantes (valeurs données) sont \(V\) et \(h\).
Le processus de résolution de \(r\) est illustré ci-dessous:
\[\large V = \pi r^2 h\] \[\large \displaystyle \Rightarrow \frac{V}{\pi h} = r^2\] \[\large \displaystyle \Rightarrow \sqrt{\frac{V}{\pi h}} = r\]Par conséquent, l'équation littérale est résolue, car nous avons \(r\) isolé d'un côté de l'égalité et le reste de l'autre côté.
EXEMPLE 2:
Résolvez l'équation littérale suivante:
\[\large m n = \frac{x-y}{k} \]pour \(x\).
RÉPONDRE:
Dans ce cas, on nous dit explicitement que la variable est \(x\), donc toutes les autres lettres sont des constantes aux fins de la résolution de l'équation.
Ce qui suit est obtenu lors de la résolution de \(x\):
\[\large m n = \displaystyle \frac{x-y}{k} \] \[\large m n k = x-y \] \[\large m n k+y = x \]ce qui termine le calcul.
En savoir plus sur la résolution d'équations littérales
Pourquoi faisons-nous un flou sur la différence entre les équations littérales et les équations régulières? En fait, nous ne faisons pas de fuzz. Une équation littérale est avant tout une équation.
L'exercice conceptuel consiste à réaliser que peu importe si nous avons un nombre ou une constante qui représente un nombre générique, le processus de résolution de l'équation est identique. C'est le concept clé.
Comment résoudre des équations littérales avec des fractions
Alors, que se passe-t-il si vous trouvez des fractions lorsque vous résolvez une équation littérale avec des fractions? Eh bien, comme vous le feriez avec une équation régulière: si vous voulez éliminer quelque chose qui est dans le dénominateur, vous multipliez les deux côtés de l'équation par lui, et si vous voulez éliminer quelque chose qui est dans le numérateur, vous divisez les deux côtés de l'équation par elle.
Y a-t-il une stratégie qui fonctionne mieux?
Pas vraiment. Selon le type d'équation dont vous disposez, vous pouvez utiliser des stratégies spécifiques pour vous faciliter la tâche. Par exemple, si vous avez un équation logarithmique (une équation dans laquelle la variable est à l'intérieur d'un logarithme), il vaut mieux utiliser efficacement le règles de journalisation pour résoudre ces équations efficacement.