En savoir plus sur ce créateur de cartes xbar

Cette calculatrice de graphique à barres X vous montrera toutes les étapes nécessaires pour construire un graphique à barres X, qui est l'un des graphiques les plus couramment utilisés pour évaluer si un processus est sous contrôle ou non.

Ceci est réalisé en identifiant graphiquement les points qui présentent un niveau de variation qui semble aller statistiquement au-delà de ce que l'on considérerait comme une "cause commune".

Quelles formules sont utilisées pour un graphique à barres x ?

Dans ce cas, nous supposons que nous avons $N$ échantillons et que chaque échantillon a une taille de $k$ (où typiquement $N$ est beaucoup plus grand que $k$).

Ainsi, pour chaque échantillon $i$, nous calculons la moyenne de l'échantillon $\bar X_i$ et l'étendue de l'échantillon $R_i$. Ensuite, on prend la moyenne de ces échantillons pour obtenir $\overline{\overline X}$ et $\bar R$

Ensuite, vous utilisez la formule suivante pour obtenir la limite de contrôle inférieure et supérieure pour le graphique X-bar

$$LCL_{\bar X} = \overline{\overline X} - A_2 \bar R$$ $$UCL_{\bar X} = \overline{\overline X} + A_2 \bar R$$

où $A_2$ est une constante qui dépend de la taille $k$ des échantillons.

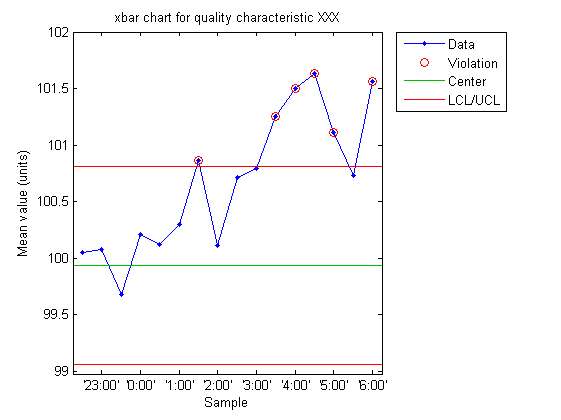
Comment faire un graphique à barres x ?

1. La première étape consiste à collecter les données, où vous collectez des échantillons, et chaque échantillon a la même taille d'échantillon.

2. Ensuite, vous calculez la moyenne et la plage d'échantillons pour chacun des échantillons.

3. Vous calculez la moyenne générale des moyennes et de la plage de l'échantillon.

4. Ensuite, vous calculez les limites de contrôle $LCL_{\bar X} = \overline{\overline X} - A_2 \bar R$ et $UCL_{\bar X} = \overline{\overline X}$ + A_2 \bar R \).

5. Maintenant, vous tracez chacune des moyennes d'échantillon dans un tracé linéaire, et vous tracez les limites inférieure et supérieure.

6. Enfin, vous évaluez si l'une des moyennes de l'échantillon dépasse ou non les limites de contrôle.

Les points qui dépassent les limites inférieure et supérieure de contrôle sont dits hors contrôle statistique. Si aucun point n'est hors contrôle statistique, alors le processus est sous contrôle.

Autre carte de contrôle

La carte Xbar est utilisée pour évaluer si le centre du processus est sous contrôle ou non. Si vous avez besoin d'évaluer si la variabilité du processus est sous contrôle statistique, vous pouvez utiliser cette Créateur de cartes R .

Pouvez-vous créer un graphique à barres x dans excel ?

Oui, vous devez construire un graphique avec trois lignes constantes (pour les limites inférieure, centrale et supérieure) et un autre graphique linéaire pour le graphique des moyennes d'échantillon.

Avec cette calculatrice, vous pouvez directement coller les données que vous avez dans Excel dans la feuille de calcul ci-dessus, pour obtenir des calculs automatiques, étape par étape.