Calculatrice d'expansion binomiale
Instructions: Vous pouvez utiliser ce calculateur de coefficient binomiel pour obtenir l'explication étape par étape de la manière d'obtenir l'expansion de \((a + b)^n\). Veuillez saisir les valeurs de \(a\), \(b\) et \(n\):
Que savoir sur cette calculatrice d'expansion binomiale
Cette calculatrice d'expansion binomiale avec étapes vous donnera une démonstration claire de savoir comment calculer l'expression \[(a+b)^n\]
Pour les nombres donnés \(a\), \(b\) et \(n\), où \(n\) est un entier.L'expression ci-dessus peut être calculée dans une séquence appelée L'expansion binomiale, et il a de nombreuses applications dans différents domaines de mathématiques.
L'expansion binomiale de l'ordre n
En utilisant diverses approches, la formule d'une expansion binomiale a été trouvée et elle est indiquée ci-dessous
\[(a+b)^n = a^n + \dbinom{n}{1} a^{n-1} b + \dbinom{n}{1} a^{n-2} b^2 + ... \dbinom{n}{n-1} a b^{n-1} + b^n\]où le terme \(\dbinom{n}{k}\) calculé est:
\[\dbinom{n}{k} = \frac{n!}{k! \times (n-k)!}\]Ce terme \(\dbinom{n}{k}\) est communément appelé le k h Coefficient binôme d'une expansion binomiale de commande \(n\).Comme on peut le voir, un L'expansion binomiale de la commande \(n\) a \(n+1\) termes, lorsque \(n\) est un entier positif.
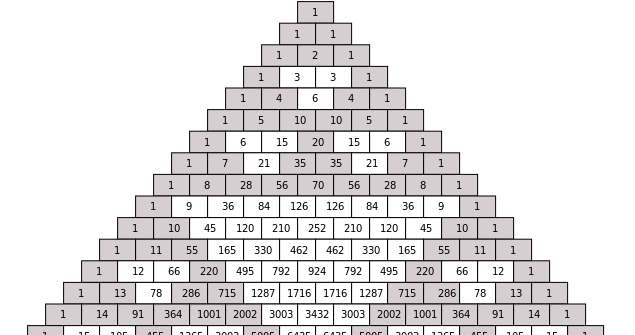
Triangle de Pascal pour une calculatrice d'expansion binomiale Puissance négative
Un moyen très intelligent et facile de calculer les coefficients d'une expansion binomiale consiste à utiliser un triangle qui commence par "1" En haut, puis "1" et "1" à la deuxième rangée.Ensuite, de la troisième rangée et à prendre "1" et "1" au début et à la fin de la rangée et le reste des coefficients peuvent être trouvés en ajoutant les deux éléments au-dessus de celui-ci, dans la rangée immédiatement au-dessus, comme indiqué dans la thécétique tableau ci-dessous.
Une calculatrice d'expansion binomiale
Jusqu'à présent, nous avons considéré l'ordre \(n\) comme un entier positif, mais il y a aussi une expansion lorsque \(n\) est négatif, seulement ce n'est pas nécessairement fini, et cela impliquera un nombre infini de termes dans le cas général.
Coefficients binomiaux
Au lieu de calculer toute l'expansion, utilisez ceci Calculateur de coefficient binomial obtenir un terme spécifique de l'expansion.