Algèbre Tutoriels

Asymptotes horizontales

Dans ce tutoriel, nous aborderons le concept de asymptote horizontale et ses applications les plus importantes. Nous essaierons d'éviter les explications trop techniques, mais quelques touches de calcul seront utilisées.

L'essentiel de ce tutoriel est d'acquérir une forte intuition géométrique sur les asymptotes horizontales. Commençons !

Qu'est-ce qu'une asymptote horizontale ?

Une asymptote horizontale est une limite supérieure, que l'on peut imaginer comme une ligne horizontale qui fixe une limite au comportement du graphique d'une fonction donnée.

Cela signifie que le graphique de la fonction \(f(x)\) s'approche en quelque sorte de cette ligne horizontale lorsque la valeur de \(x\) augmente.

Comment trouver l'asymptote horizontale ?

Comprendre ce comportement horizontal limite des fonctions qui présentent cette caractéristique peut s'avérer très utile pour trouver des asymptotes horizontales.

En effet, dans certaines circonstances, ce comportement limite ressemble beaucoup à celui d'une ligne horizontale pour de grandes valeurs de \(x\). Voir la fonction ci-dessous à titre d'exemple.

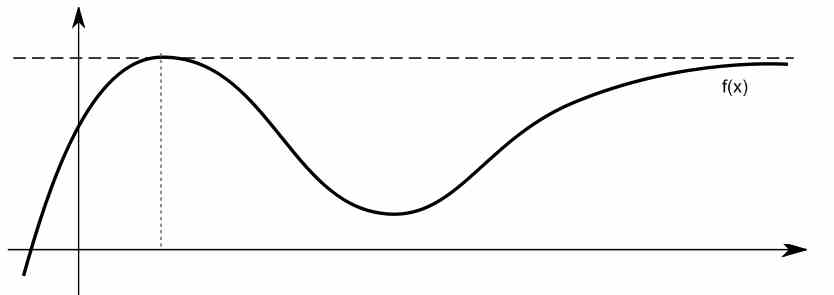
Comment trouver l'asymptote horizontale d'une fonction en utilisant les limites ?

Pour que la définition soit claire, une ligne horizontale \(y = h\) est une asymptote horizontale de la fonction \(f(x)\) si

\[\large \lim_{x\to\infty} f(x) = h\]

si la limite ci-dessus existe et si elle est finie. Pour ceux qui n'ont pas encore suivi de cours de calcul, la ligne horizontale \(y = h\) est une asymptote horizontale de la fonction \(f(x)\) lorsque \(h\) est le limite de \(f(x)\) lorsque \(x\) s'approche de l'infini. Que signifie être une "limite" ? Cela signifie que pour des valeurs suffisamment grandes de \(x\), la valeur de \(f(x)\) sera aussi proche de \(h\) que nous l'avons prédéfini. Impressionnant, n'est-ce pas ?

Quelle est la formule de l'asymptote horizontale ?

Pour trouver la formule de l'asymptote horizontale, nous devons d'abord trouver la limite correspondante. Supposons que vous ayez

\[\large \lim_{x\to\infty} f(x) = h\]

Dans ce cas, nous dirons que l'asymptote horizontale est \(h\), et la formule de l'asymptote horizontale est \(y = h\). En d'autres termes, l'asymptote horizontale est une simple ligne horizontale, c'est-à-dire une ligne dont la pente est nulle.

Cela donne le sens de ce que signifie une asymptote horizontale en termes de limites : la limite trouvée correspond à la définition de la ligne horizontale que l'on appelle l'asymptote horizontale.

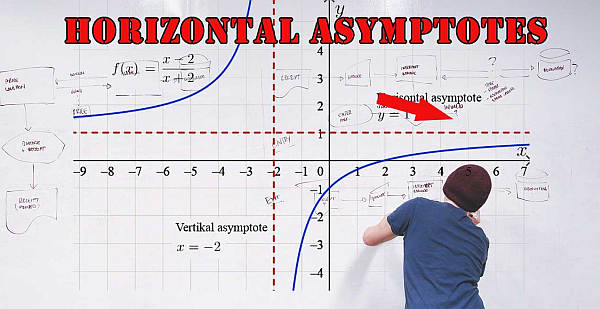
Exemple 1

Trouver une asymptote horizontale pour la fonction

\[ \large f(x) = \frac{x^2}{x^2+1} \]

Réponse:

Pour trouver l'asymptote horizontale, nous devons trouver la limite de la fonction \(f(x)\) lorsque \(x\) s'approche de l'infini. Si vous n'êtes pas familier avec le calcul, vous devriez d'abord essayer d'évaluer la fonction à une très grande valeur de \(x\).

Par exemple, disons que \(x = 1,000,000\). Introduisons ce nombre dans la fonction :

\[ \large f(1,000,000) = \frac{1,000,000^2}{1,000,000^2+1} = \frac{1,000,000,000,000}{1,000,000,000,000+1}\] \[ = \frac{1,000,000,000,000}{1,000,000,000,001} = 0.999999999999 \]

qui est très proche de 1. On devrait donc soupçonner que la limite est 1. En fait, il s'avère que lorsque \(x\) est grand, la valeur de \(x^2\) est si grande par rapport à 1, que \(x^2\) est très similaire à \(x^2 + 1\), du moins en termes relatifs. En divisant le numérateur et le dénominateur par \(x^2\), on obtient donc

\[ \large f(x) = \frac{x^2}{x^2+1} = \frac{1}{1+\frac{1}{x^2}} \rightarrow \frac{1}{1+0} = 1 \]

car \(\frac{1}{x^2}\) se rapproche de 0 lorsque \(x\) se rapproche de l'infini. Il n'est donc pas difficile de prouver ou d'être convaincu que

\[\large \lim_{x\to\infty} f(x) =\large \lim_{x\to\infty} \frac{x^2}{x^2+1} = 1\]

ce qui signifie que l'asymptote horizontale est \(y = 1\). Faites attention à votre réponse si vous répondez à un test ou à un devoir. Certaines personnes diront "l'asymptote horizontale est 1", ce qui est faux.

Techniquement, l'asymptote horizontale est la fonction \(y = 1\), et NON le nombre 1. L'asymptote horizontale est une fonction qui est constante, ce qui n'est pas la même chose qu'un nombre. Je le dis simplement, parce qu'il y a des élèves difficiles.

Exemple 2

Trouver une asymptote horizontale, si elle existe pour la fonction

\[ \large f(x) = \frac{x^3}{x^2+1} \]

Réponse:

En divisant le numérateur et le dénominateur par \(x^2\) :

\[ \large f(x) = \frac{x}{1+\frac{1}{x^2}} \]

Mais attendez ! L'astuce n'a pas fonctionné ici ? Si, elle a fonctionné. Remarquez que le dénominateur devient très proche de 1 lorsque \(x\) devient très grand, et que le numérateur devient très grand.

Il n'est pas difficile de croire que \(f(x)\) converge vers l'infini, de sorte qu'il n'y a pas d'asymptote horizontale. Chaque fois qu'une fonction n'est pas bornée, comme c'est le cas pour \(f(x)\) dans cet exemple, il n'y a pas d'asymptote horizontale.

Asymptote horizontale ou asymptotes horizontales ?

Techniquement, il peut y avoir deux asymptotes horizontales, l'une à gauche et l'autre à droite. L'asymptote horizontale gauche est \(y = h_L\) si

\[\large \lim_{x \to -\infty} f(x) = h_L\]

De même, l'asymptote horizontale droite est \(y = h_R\) si

\[\large \lim_{x \to +\infty} f(x) = h_R\]

dans le cas où l'une des limites ci-dessus existe et est finie. Il peut arriver qu'une fonction ait deux asymptotes horizontales, une seule asymptote horizontale ou aucune asymptote horizontale.

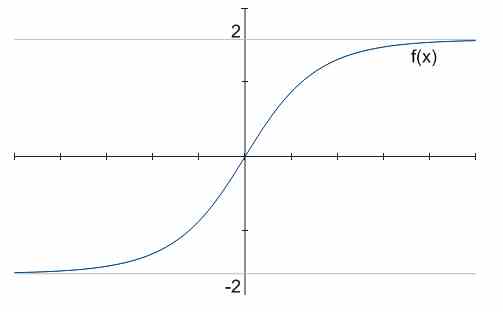
Par exemple, dans le graphique ci-dessus, il y a deux asymptotes horizontales, \(y = -2\) et \(y = 2\).

Quelle est la règle pour trouver l'asymptote horizontale ?

Il n'existe pas de règles générales applicables à tous les cas. Dans le cas général, nous devons calculer la limite lorsque \(x\) s'approche de \(-\infty\), et la limite lorsque \(x\) s'approche de \(+\infty\).

Si l'une de ces limites existe et est finie, nous aurons les asymptotes horizontales.

Une règle spécifique peut être élaborée pour le cas où la fonction donnée \(f(x)\) est le quotient de deux polynômes. Dans ce cas, supposons que \(m\) est l'ordre du polynôme au numérateur, et que \(n\) est l'ordre du polynôme au dénominateur. Nous avons alors les cas suivants :

Cas 1 : Si \(m < n\), l'asymptote horizontale est \(y = 0\).

Cas 2 : Si \(m = n\), et \(a\) est le coefficient directeur du polynôme au numérateur, et \(b\) est le coefficient directeur du polynôme au dénominateur, alors l'asymptote horizontale est \(\displaystyle y = \frac{a}{b}\).

Cas 3 : Si \(m > n\), il n'y a pas d'asymptote horizontale.

Exemple 2

Trouver, si elle existe, l'asymptote horizontale de la fonction

\[\large f(x) = \frac{3x^2+2x-1}{2x^2 -x+2}\]

Réponse:

La fonction est le quotient de deux polynômes. Le polynôme au numérateur est \(3x^2+2x-1\), qui est un polynôme d'ordre 2, donc \(m = 2\), et à coefficients premiers 3.

Le polynôme au dénominateur est \(2x^2 -x+2\), qui est un polynôme d'ordre 2, donc \(n = 2\), et la constante de tête 2. Vous pouvez utiliser notre Calculatrice polynomiale pour réaliser cette division en montrant toutes les étapes.

Ainsi, puisque dans ce cas \(m = n\), il y a une asymptote horizontale, et qu'elle est le quotient des coefficients premiers, alors dans ce cas, l'asymptote horizontale est

\[\large y = \frac{3}{2}\]

En savoir plus sur les asymptotes horizontales

Ta question est donc de savoir comment trouver les asymptotes d'une équation, n'est-ce pas ? Tout d'abord, on trouve les asymptotes d'une fonction et non d'une équation. Il faut donc commencer par la définition générale, en utilisant les limites.

Si vous ne connaissez pas le calcul et ne savez pas comment calculer les limites, vous devriez au moins essayer d'introduire de très grandes valeurs de \(x\), ainsi que des valeurs très négatives de \(x\) sur la fonction, et voir comment la fonction se comporte.

Même en traçant la fonction à l'aide d'un logiciel, vous pouvez savoir s'il existe des asymptotes horizontales.

En définitive, dans le cas très restreint où la fonction est une quotient de polynômes vous pouvez alors appliquer la règle sur la base des ordres \(m\) et \(n\).