Calculadora de fórmula de ponto médio

Esta calculadora permitirá que você encontre o ponto médio entre dois pontos. Basta fornecer as coordenadas dos dois pontos e clicar em “Calcular” para obter todos os passos mostrados.

Em primeiro lugar, precisamos lembrar que o distância entre dois pontos no plano euclidiano baseia-se no conceito dos princípios geométricos básicos que permitem a utilização do teorema de Pitágoras.

Como você calcula o ponto médio?

Conceitualmente falando, o ponto médio é o ponto que está a meio caminho entre os dois pontos. Esta ideia de meio caminho está de acordo com os teoremas geométricos da proporcionalidade.

O ponto médio é um par ordenado que está a meio caminho entre dois pontos dados. Essa é a primeira coisa que você precisa saber: algumas pessoas pensam erroneamente em uma quantidade como o ponto médio e, na verdade, o que você está procurando é um par ordenado.

O ponto médio para os pontos dados \((x_1, y_1)\) e \((x_2, y_2)\) é dado pela seguinte fórmula:

\[ \left( x_M, y_M \right) = \displaystyle \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right) \]

Explicação da fórmula do ponto médio

Definição De Fórmula: A fórmula do ponto médio acima está intimamente relacionada com o fórmula de distância . Na verdade, o que a fórmula acima faz é simplesmente calcular a média das duas coordenadas correspondentes.

Isto é, a primeira coordenada do ponto médio é a média das primeiras coordenadas dos dois pontos dados, e a segunda coordenada do ponto médio é a média das segundas coordenadas dos dois pontos dados. Como usar a fórmula acima? Por favor, verifique os exemplos abaixo.

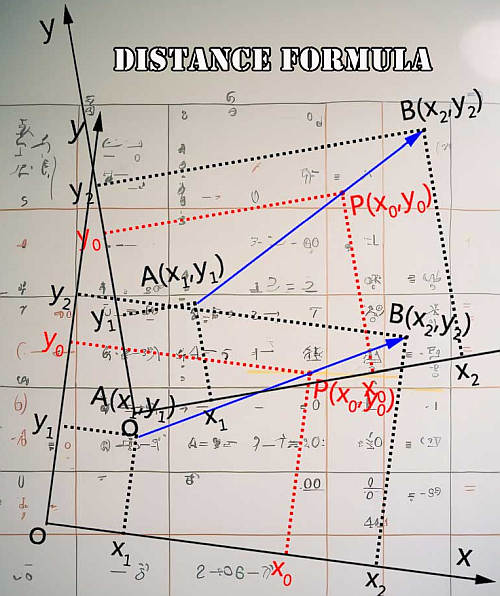
Para que uso a fórmula do ponto médio?

A ideia de ponto médio nos é tão familiar porque está intimamente associada à ideia de “meio caminho” de um ponto a outro. Situações assim são muito comuns na vida real, onde podemos ter interesse em dividir algo, por exemplo.

Naturalmente, o processo de divisão de algo não precisa necessariamente envolver um ponto médio, mas geralmente, ao fazer uma divisão igual, isso acontecerá.

Então, a fórmula do ponto médio é tão útil em parte porque é uma forma de usando a fórmula da distância em um caso muito especial, onde o ponto que encontramos está à mesma distância de ambos os pontos dados.

Exemplos de fórmulas de ponto médio

Suponha que temos dois pontos \((1, 3)\) e \((4, 8)\), então a fórmula do ponto médio é calculada da seguinte forma:

\[ \left( x_M, y_M \right) = \displaystyle \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right) = \left( \frac{1 + 4}{2}, \frac{3+ 8}{2} \right) = \left( \frac{5}{2}, \frac{11}{2} \right) \]

Às vezes você deixa a resposta como uma fração, ou às vezes você é instruído a calcular a resposta com decimais, caso em que o ponto médio seria (2,5, 5,5) no exemplo anterior.

Mais exemplos de ponto médio

Como lidar com a fórmula do ponto médio com frações? É o mesmo procedimento. Suponha que temos dois pontos \((\frac{1}{2}, \frac{1}{4})\) e \((\frac{3}{5}, \frac{3}{4})\), então o ponto médio é calculado como:

\[ \left( x_M, y_M \right) = \displaystyle \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right) = \left( \frac{1/2 + 3/5}{2}, \frac{1/4+ 3/4}{2} \right) = \left( \frac{11/10}{2}, \frac{1}{2} \right) = \left( \frac{11}{20}, \frac{1}{2} \right) \]

Isso tem a ver com pitágoras?

Quase tudo tem a ver Pitágoras . O ponto médio da hipotenusa se projetará no ponto médio dos catetos para um triângulo retângulo. Além disso, você pode pegar os dois pontos e calcular o distância entre eles , usando a fórmula pitagórica.