Come trovare l'inverso di una funzione
Molte applicazioni in Algebra e Calcolo dipendono dal sapere come trovare l'inverso di una funzione, e questo è l'argomento di questo tutorial.
Prima di tutto, devi capire che prima di trovare l'inverso di una funzione, devi assicurarti che tale inverso esista.
La cosa buona del metodo per trovare l'inverso che useremo è che troveremo l'inverso e scopriremo se esiste o meno allo stesso tempo.
Pronto?? Allora allaccia le cinture.
Come puoi sapere se una funzione ha un inverso?
Tecnicamente, una funzione ha un inverso quando è uno-a-uno (iniettiva) e suriettiva.
La condizione cruciale però è che deve essere uno a uno, perché una funzione può essere resa suriettiva restringendo il suo raggio d'azione alla propria immagine.
Come fai a sapere quando una funzione è uno a uno?
Bene, ci sono almeno un paio di modi. Uno è il modo algebrico e l'altro è il modo grafico (scommetto di sapere quale preferisci, eh?)
Modo algebrico
Per il modo algebrico, affinché una funzione \(f\) sia uno-a-uno, dobbiamo dimostrare che ogni volta che \(f(x) = f(y)\), abbiamo bisogno di \(x = y\).
In altre parole, dobbiamo dimostrarlo
\[f(x) = f(y) \,\,\Rightarrow \,\, x = y\]
Modo grafico
Per il modo grafico, dobbiamo usare il test della linea orizzontale : Per qualsiasi linea orizzontale che disegniamo, il grafico della funzione attraversa al massimo una volta quella linea orizzontale.
Graficamente:
Supera il test della linea orizzontale
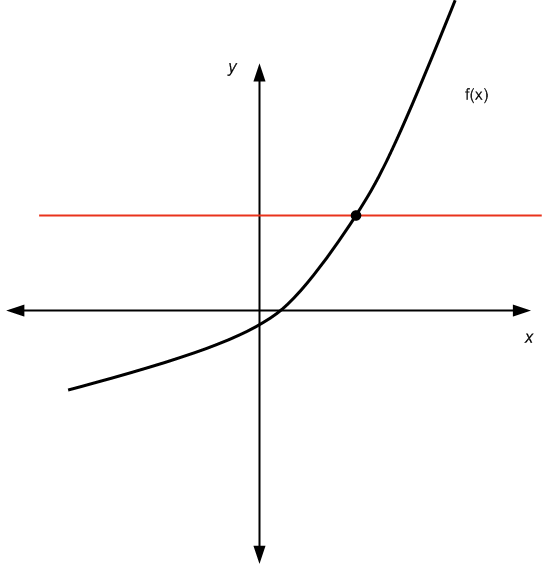
Non supera il test della linea orizzontale
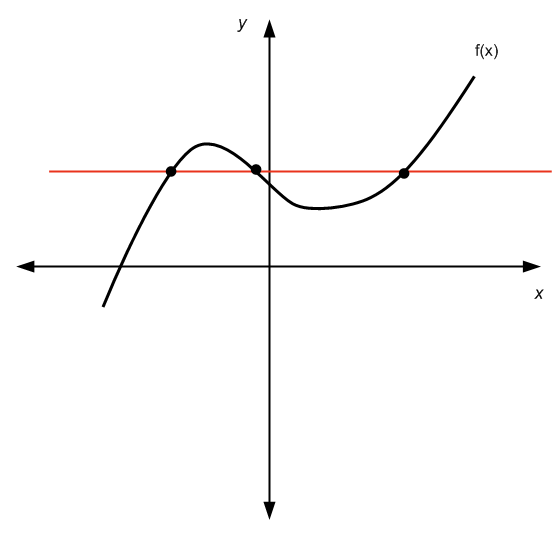
Trovare l'inverso
Trovare l'inverso di una data funzione \(f(x)\) richiede di risolvere un'equazione.
In effetti, hai l'equazione \(f(x) = y\), prendi \(y\) come un dato numero e devi risolverlo per \(x\) e devi assicurarti che la soluzione sia UNICA.
Questo è tutto. Facile, vero ??
Ora, passiamo ai passaggi pratici:
Passo 1:
Per un dato \(y\), imposta l'equazione:
e risolverlo per \(x\).
Passo 2:
Assicurati di prestare attenzione per vedere per quale \(y\), in realtà esiste una soluzione unica.
Passaggio 3:
Una volta risolto \(x\) in termini di \(y\), l'espressione che dipende da \(y\) sarà il tuo \(f^{-1}(y)\).
Passaggio 4:
Cambia il nome della variabile da \(y\) a \(x\) e avrai la tua funzione inversa \(f^{-1}(x)\).
ESEMPIO 1
Trova l'inverso della funzione \(f(x) = \sqrt x\)
RISPOSTA:
Quindi, prendiamo \(y\) come dato e dobbiamo risolvere \(f(x) = y\), che in questo caso corrisponde a risolvere
\[\sqrt x = y\]Nota che la radice quadrata è sempre non negativa, quindi per avere una soluzione, abbiamo bisogno di \(y\ge 0\).
Applicando il quadrato su entrambi i lati lo otteniamo
\[\Rightarrow \,\, (\sqrt x)^2 = y^2\] \[\Rightarrow \,\, x = y^2\]Quindi, \(f^{-1}(y) = y^2\), e cambiando il nome della variabile, abbiamo la funzione inversa is
\[f^{-1}(x) = x^2\]per \(x\ge 0\).
ESEMPIO 2
Trova l'inverso della funzione \(f(x) = \displaystyle \frac{x}{x+1}\), per \(x > -1\)
RISPOSTA:
Di nuovo, prendiamo \(y\) come dato, e ora dobbiamo risolvere per \(x\) l'equazione \(f(x) = y\). Quindi abbiamo
\[\displaystyle \frac{x}{x+1} = y\] \[\Rightarrow \,\, x = y(x+1)\] \[\Rightarrow \,\, x = yx + y\] \[\Rightarrow \,\, x - yx = y\] \[\Rightarrow \,\, x(1 - y) = y\] \[\Rightarrow \displaystyle \,\, x = \frac{y}{1-y}\]Quindi, \(f^{-1}(y) = \displaystyle \frac{y}{1-y}\), e cambiando il nome della variabile, abbiamo la funzione inversa is
\[f^{-1}(x) = \displaystyle \frac{x}{1-x}\]Ulteriori informazioni sulla ricerca dell'inverso di una funzione
Una delle proprietà cruciali della funzione inversa \(f^{-1}(x)\) è che \(f(f^{-1}(x)) = x\).
Pensa a cosa sta dicendo questa cosa. Qualcosa del tipo: "La funzione valutata al contrario ti dà l'identità".
In altre parole, valutare l'inverso tramite la funzione è come non fare nulla all'argomento.
O come alcune persone amano dire: la funzione può annullare l'inverso in un modo.
Scegli la tua versione.
Come trovare l'inversa di una funzione quadratica? Puoi?
In realtà, la risposta è: dipende. Questo perché se consideriamo una funzione quadratica su tutta la linea reale , quindi non è 1 a 1, poiché non supera il test della linea orizzontale, come puoi vedere nella tabella seguente:
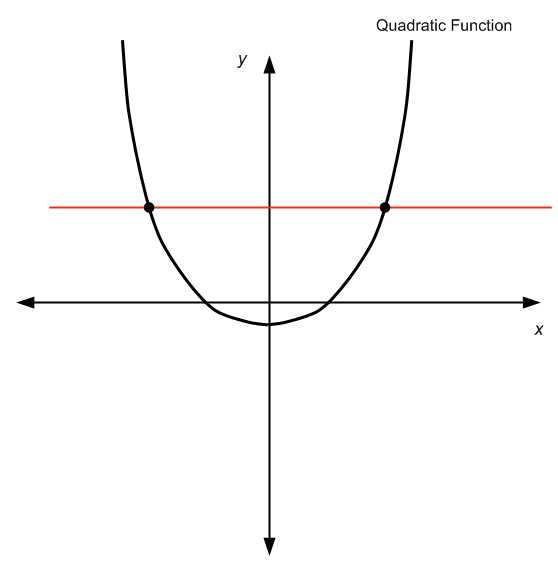
Non superando il test della linea orizzontale, possiamo vedere che per un dato \(y\) c'è più di un valore \(x\) così che \(f(x) = y\), quindi non possiamo "risolvere" per \(x\), poiché c'è più di un \(x\).
MA, se limiti il dominio e consideri solo i numeri positivi, otterremmo quanto segue:
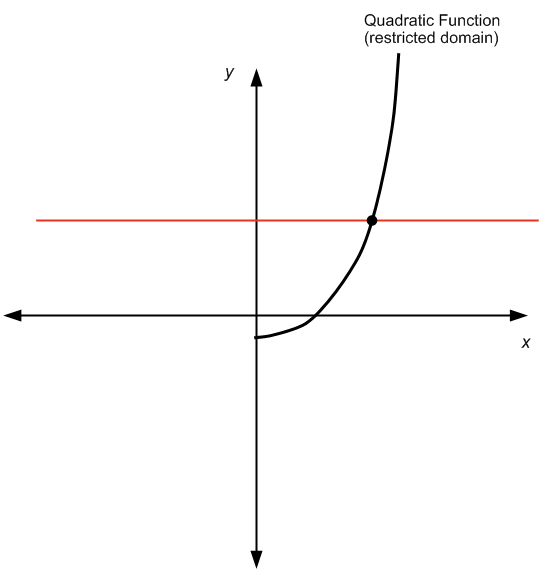
che supera il test della linea orizzontale e quindi la funzione quadratica è invertibile.
MORALE DELLA STORIA: Per verificare se qualcosa è invertibile, NON si tratta solo della funzione. Riguarda la funzione E la sua dominio e intervallo .
Come capire rapidamente il grafico delle funzioni inverse
C'è sempre la necessità di valutare se la funzione \(f(x)\) è invertibile o meno (controllando se è uno a uno o meno). Ma supponendo che tu sappia che è invertibile, c'è un modo semplice per trovare il grafico dell'inverso.
Innanzitutto, rappresenta graficamente la funzione data \(f(x)\).
Quindi, tracciare un grafico della linea dei 45 gradi \(y = x\).
Per rappresentare graficamente \(f^{-1}(x)\), tutto ciò che devi fare è riflettere il grafico di \(f(x)\) attraverso la linea dei 45 gradi \(y = x\), come uno specchio.
Vedi l'esempio sotto con le funzioni \(f(x) = \sin x\) e \(f^{-1}(x) = \arcsin x\)
Un altro modo per vederlo è usare l'originale grafico e modificare il valore di \(x\) con il valore di \(y\).
C'è un modo per una funzione di essere la propria inversa?
Sì, in realtà è possibile, ma succede solo per la funzione identità, cioè con \(f(x) = x\).