Il grafico di una funzione è un insieme di coppie ordinate \((x,y)\). Oppure, il grafico di una funzione è una concettualizzazione che facciamo un insieme di coppie \((x,y)\) su un sistema di coordinate. Dico che è una concettualizzazione, perché il modo in cui rappresentiamo un grafico è in una certa misura un'illusione ottica.

Perché lo dico? Bene, dai un'occhiata. A cosa pensi quando dico "grafico". Controlla la figura prima.

Quindi questo è un grafico. Un insieme di coppie \((x, y)\), o come possiamo anche chiamarle, punti. Di seguito viene evidenziato un punto specifico, dai un'occhiata

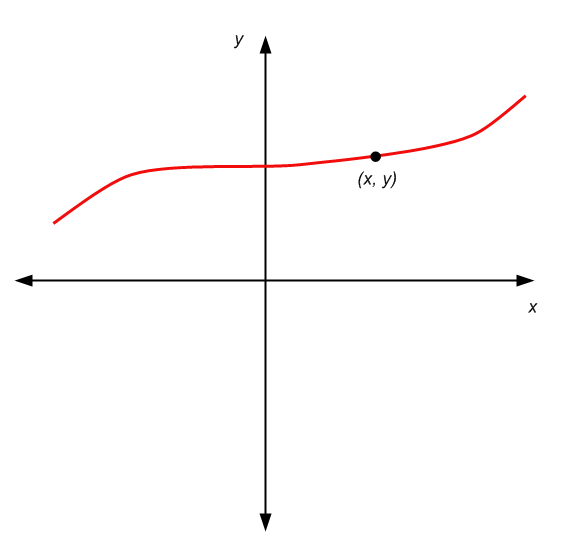
Il trucco, o l'illusione visiva, è che un punto non ha, in teoria, dimensioni (né larghezza, né lunghezza). Quindi questa "curva" che disegniamo per rappresentare un grafico, è una specie di modo conveniente per rappresentare un grafico, ma siamo una specie di barare, perché questa rappresentazione ha una curva che ha uno spessore.

Quindi, questo non è per piovere sulla tua parata, è solo per chiarire che quello che intendi come un grafico, è piuttosto un rappresentazione di un grafico conveniente e credibile.

Grafici associati alle funzioni

Un modo davvero semplice per definire un grafico è usare una funzione \(f(x)\). Infatti, un grafico definito da una funzione \(f(x)\) è l'insieme di tutti i punti \((x, f(x))\), per \(x \in D\), dove \(D\) è il dominio della funzione \(f\).

La rappresentazione è la stessa dei grafici precedenti, solo che ora facciamo quanto segue:

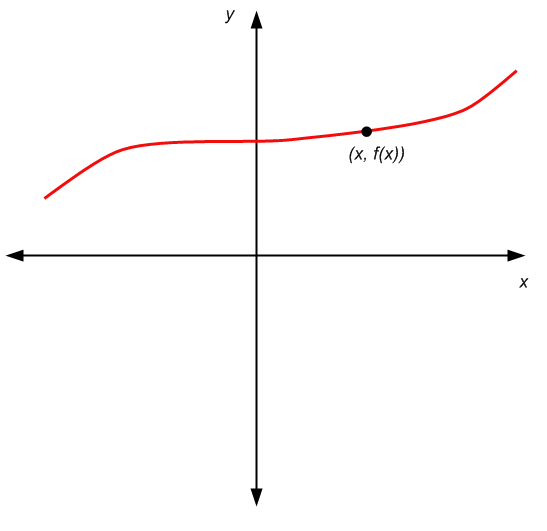
In questo caso, la differenza più evidente è che il secondo componente della coppia \((x,y)\) non è un valore qualsiasi \(y\). Il secondo componente è \(f(x)\), quindi è determinato in modo univoco da \(x\).

ESEMPIO 1

Traccia il grafico della funzione \(f(x) = x^2\).

RISPOSTA:

Niente di strano, dobbiamo solo disegnare il grafico di una funzione. I punti nel grafico hanno la forma \((x, f(x)) = (x, x^2)\). Questo significa che il valore di \(x\) è associato a \(x^2\) sul grafico.

Esempi di punti che si trovano sul grafico: \((1, 1)\), \((2, 2^2) = (2, 4)\), \((3, 3^2) = (3, 9)\), ecc. Graficamente otteniamo la seguente rappresentazione del grafico:

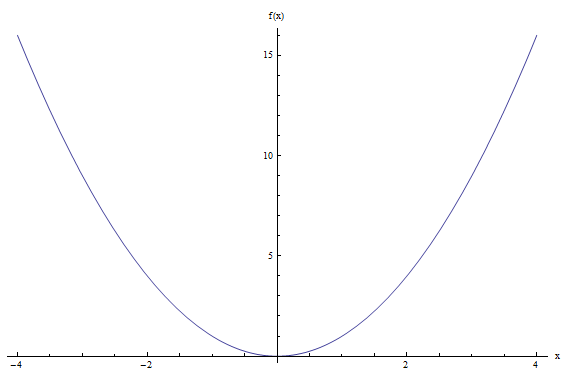
Grafici continui e discontinui

Una delle ipotesi che facciamo nella nostra mente quando pensiamo a un grafico è che sia fluido, senza salti. Questo non è sempre il caso. Ci sono funzioni che portano a funzioni che saltano, o addirittura portano ad essere grafici. Altre funzioni hanno grafici molto fluidi, come è successo con \(f(x) = x^2\).

Il concetto di levigatezza di una funzione è formalmente trattato in Calculus, con la nozione di funzione continua. Ma senza troppa confusione, possiamo dire che, per ora, penseremo che una funzione continua è una funzione che ha un grafico "regolare" e una funzione discontinua è una funzione che non è liscia, o ha "salti".

ESEMPIO 2

La funzione \(f(x) = sin(x)\) è continua?

RISPOSTA:

Ebbene, ancora una volta, avremmo bisogno di un'analisi formale della continuità per verificare. Ma alla luce della definizione informale data sopra, controlliamo il suo grafico. Il computer ci dà quanto segue:

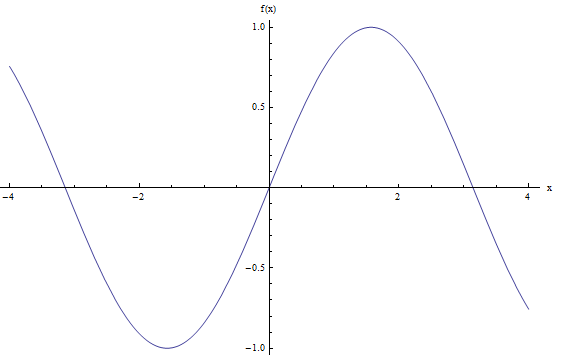
Direi che il grafico sopra sembra molto fluido, senza salti, quindi usando la nostra definizione ingenua, direi che \(f(x) = \sin x\) è continuo.

ESEMPIO 3

La funzione \( f\left( x \right)=\left\{ \begin{array}{cc}-1 &\,\,\,\,\text{for } x\le 1 \\ \\ x & \,\,\,\,\,\,\text{for }x>1 \\ \end{array} \right.\) è continua?

RISPOSTA:

Per rispondere alla domanda, dobbiamo tracciare il grafico. Il computer ci dà quanto segue:

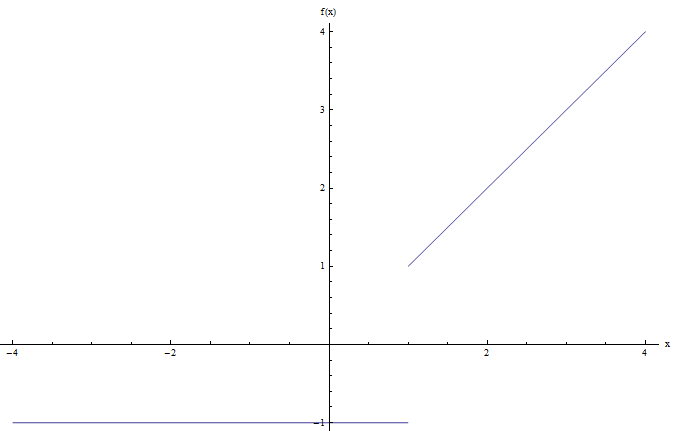
Si noti che c'è un salto nel punto \(x = 1\), quindi direi che il grafico sopra ha un salto e quindi questa funzione è discontinua.

Ulteriori informazioni sui grafici

L'utilizzo di grafici per creare una rappresentazione di una funzione può svolgere un ruolo cruciale per comprendere il comportamento di una funzione.

Ci sono abbastanza strumenti analitici (Calculus) per capire il comportamento di una funzione \(f(x)\), senza bisogno di tracciarla. Tuttavia, è molto pratico vedere un grafico perché è un modo molto rapido per avere un'idea di cosa sta facendo la funzione.

Osserva che non tutti i grafici devono provenire da funzioni. Ad esempio, i grafici possono anche derivare da relazioni. Guarda il grafico sotto e dimmi se riesci a scoprire quale relazione è associata ad esso.

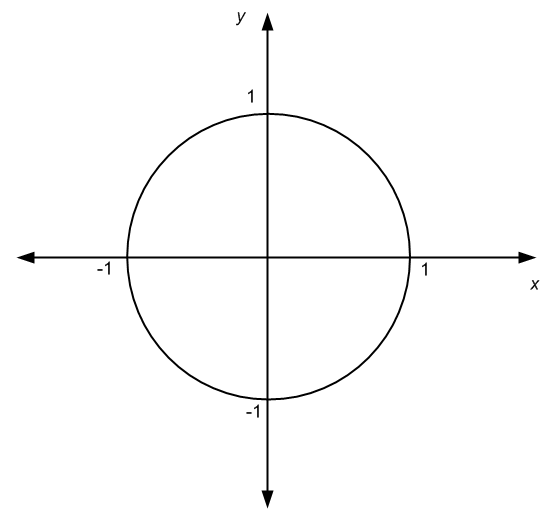
Hai capito bene, quel grafico sopra è la rappresentazione dell'equazione di un cerchio unitario, \(x^2 + y^2 = 1\), che come già sappiamo, determina una relazione e non una funzione.

Se hai bisogno di costruire un grafico, provalo grafico di funzioni per avere una buona rappresentazione di come si svolge la funzione.