Come trovare il dominio
Imparare a trovare il dominio di una funzione è un'abilità cruciale in Algebra, perché ti dà la capacità di valutare dove una funzione è correttamente definita. O in altre parole, la regione in cui è valido per operare la funzione
Il compito di trovare dove è valido per operare una funzione è utile. Ad esempio, considera la funzione \(f(x) = \sqrt x\). Sappiamo che la funzione utilizza valori tali che \(x \ge 0\). Non possiamo lavorare con numeri negativi, perché otterremmo qualcosa come \(f(-1) = \sqrt{-1}\), che non è ben definito (almeno come numero reale)
Puoi controllare il nostro precedente tutorial in cui abbiamo parlato in modo approfondito del dominio e intervallo . Questo tutorial sarà orientato alla parte operativa della ricerca del dominio.
Perché dobbiamo trovare il dominio?
Il motivo per cui abbiamo bisogno di trovare il dominio di una funzione è che ogni funzione ha uno specifico insieme di valori in cui è definita. Non tutte le funzioni sono definite ovunque nella linea reale.
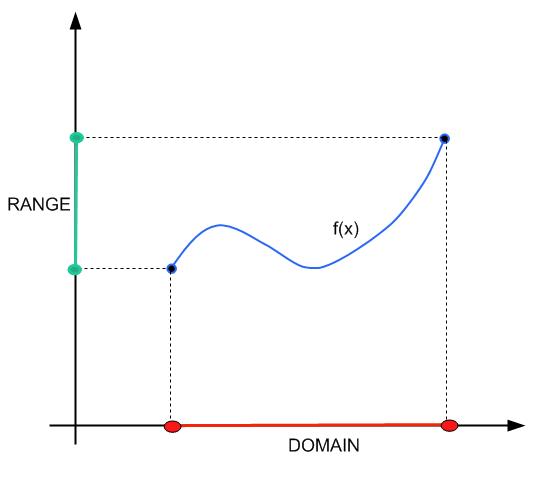
Il dominio della regione nella linea reale in cui si trova valido per lavorare con la funzione \(f(x)\), in termini di valori che \(x\) può assumere.
Cosa dobbiamo fare per trovare il dominio?
In realtà, non esiste un trucco che si adatti a tutte le taglie. Ogni funzione è diversa e devono essere utilizzate strategie diverse per trovare il dominio, a seconda della funzione.
Ci sono due tecniche che devi SEMPRE tenere in considerazione:
Tecnica 1
: Assicurati che ci siano divisioni per zero.
Inoltre, quei punti che portano a una divisione per zero devono essere esclusi dal dominio.
Tecnica 2
: Assicurati che ci siano radici quadrate delle divisioni con argomenti negativi (come \(\sqrt{-1}\)).
Inoltre, quei punti che portano a una radice quadrata di un numero negativo devono essere esclusi dal dominio.
In definitiva, usando queste due tecniche dovresti essere in grado di eliminare i punti che non sono nel dominio. Il resto dei punti nella linea reale SONO parte del dominio, semplicemente.
Quindi, queste due tecniche risolvono il problema di sapere come trovare algebricamente il dominio di una funzione. Un altro modo per farlo è guardare il grafico, se disponibile.
ESEMPIO 1
Trova il dominio della funzione \(f(x) = \sqrt{x+4}+3\)
RISPOSTA:
La prima cosa che dobbiamo fare, ed è qui che risiede il nostro successo nel trovare il dominio, è determinare dove potenzialmente potremmo trovare operazioni non valide, come divisioni per zero o radici quadrate negative.
Per la funzione \(f(x) = \sqrt{x+4}+3\), non ci sono potenziali divisioni per zero, ma c'è una radice quadrata. Per avere un argomento valido, l'argomento all'interno della radice quadrata deve essere non negativo.
Pertanto, affinché \(x\) sia nel dominio della funzione, dobbiamo avere \(x\ge 0\). Ciò implica che il dominio di \(f\) è \(\{x: x\ge 0\}\) o \([0, +\infty)\) se usiamo la notazione dell'intervallo.
È sempre così facile? Non proprio, può diventare difficile quanto si ottiene, a seconda della complessità della funzione \(f(x)\).
Normalmente, però, gli esempi che vedi nei tuoi test e compiti sono piuttosto semplici. Cerchiamo di raggiungere una tacca più alta in termini di difficoltà.
ESEMPIO 2
Ora trova il dominio della funzione \(\displaystyle f(x) = \sqrt{\frac{x+4}{x-3}}\)
RISPOSTA:
Questa funzione è un po 'più complessa e richiede un trattamento più attento. In questo caso, dobbiamo preoccuparci di entrambe le possibili divisioni per zero e radici quadrate negative.
Innanzitutto, potrebbe esserci una potenziale divisione per zero, quando \(x = 3\), che indica che \(x = 3\) deve essere escluso dal dominio.
Ora, dobbiamo occuparci di una potenziale radice quadrata negativa. Dobbiamo valutare il segno di \(\displaystyle \frac{x+4}{x-3}\). Inoltre, abbiamo bisogno che non sia negativo, quindi dobbiamo risolvere:
\[\displaystyle \frac{x+4}{x-3} \ge 0\]Affinché una divisione sia non negativa, è necessario che sia il numeratore che il denominatore siano positivi, oppure sia il numeratore che il denominatore siano negativi.
In altre parole, abbiamo bisogno che sia \(x+4 \ge 0\) e \(x-3 > 0\), o entrambi \(x+4 \le 0\) e \(x-3 < 0\).
È lo stesso che sia \(x \ge -4\) che \(x > 3\) o entrambi \(x \le -4\) e \(x < 3\).
E questo può essere scritto come \(x > 3\), o entrambi \(x \le -4\), che corrisponde all'intervallo \( (-\infty, -4] \cup (3, +\infty)\).
La conclusione è che il dominio della funzione \(\displaystyle f(x) = \sqrt{\frac{x+4}{x-3}}\) è:
\[ dom(f) = (-\infty, -4] \cup (3, +\infty)\]Come puoi vedere, il livello di difficoltà è aumentato leggermente e puoi effettivamente aumentarlo quanto vuoi.
Come trovare il dominio di una funzione razionale
Prima di tutto, ricordiamo che una funzione razionale è il quoziente di due polinomi, della forma:
\[f(x) = \frac{p(x)}{q(x)} = \frac{a_0 + a_1 x + ...+ a_m x^m}{b_0 + b_1 x + ...+ b_n x^n}\]Come trovi il dominio per la funzione razionale di cui sopra? Dobbiamo seguire la nostra regola: cercare potenziali divisioni per zero e radici quadrate negative.
In questo caso, non ci sono potenziali radici quadrate negative, ma potrebbero esserci divisioni per zero, ovunque il polinomio che si trova nel denominatore sia zero.
La conclusione è molto semplice: il dominio di una funzione razionale è l'intera retta reale TRANNE quei punti in cui il polinomio al denominatore è zero.
ESEMPIO 3
Trova il dominio di
\[f(x) = \frac{x^2 + x + 1}{x^3 - 6x^2 + 11x - 6}\]RISPOSTA:
Prima di tutto, dobbiamo capire che questa è una funzione razionale, perché hai due polinomiali \(p(x) = x^2 + x + 1\) e \(q(x) = x^3 - 6x^2 + 11x - 6\) rispettivamente al numeratore e al denominatore.
Quindi, il primo passo è trovare gli zeri del polinomio nel denominatore, quindi dobbiamo risolvere: \[ x^3 - 6x^2 + 11x - 6 = 0\]
Quell'equazione è un po 'difficile da risolvere, quindi ti darò davvero \(x^3 - 6x^2 + 11x - 6 = (x-1)(x-2)(x-3)\), quindi dobbiamo risolvere:
\[ x^3 - 6x^2 + 11x - 6 = (x-1)(x-2)(x-3) = 0\]il che significa che le radici del polinomio nel denominatore sono \(x_1 = 1, x_2 = 2, x_3 = 3\). La conclusione è che il dominio della funzione è l'intera linea reale, ad eccezione dei punti 1, 2 e 3. Usando la notazione dell'intervallo, il dominio è \((-\infty, +\infty) \backslash \{1,2,3\}\).
Altre strategie per trovare il dominio di una funzione
L'alternativa di trovare il dominio di una funzione guardando le potenziali divisioni per zero o radici quadrate negative, che è il modo analitico, è guardare il grafico.
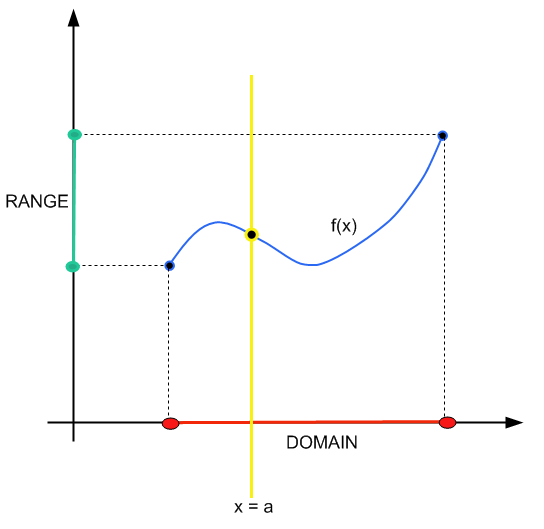
Il metodo è semplice: costruisci una linea verticale \(x = a\). Se quella linea verticale attraversa il grafico della funzione in un solo punto, allora \(x = a\) appartiene al dominio.
Breve e dolce.
Infine, come trovare il dominio di una funzione con radice quadrata
This è il nucleo di una delle tecniche di cui abbiamo parlato, ovvero trovare potenziali radici quadrate negative. Quindi, quando hai una funzione con una o più radici quadrate, sai che è molto probabile che tu abbia una potenziale radice negativa e devi rilevarla.
Tuttavia, non è sempre così. Pensa alla funzione \(f(x) = \sqrt{x^2}\). Quella funzione ha una radice quadrata, ma l'argomento all'interno è \(x^2\), che non può essere negativo, quindi abbiamo un caso di una funzione con una radice quadrata che non ha radici quadrate negative.