Algebra Tutorial

Il teorema binomiale

Il teorema binomiale è uno dei teoremi più famosi in algebra e ha una moltitudine di applicazioni nei campi di algebra, probabilità e statistica. Indica una formula simpatica e concisa per il n ^th potenza della somma di due valori: $(a+b)^n$

Sono stato presentato per la prima volta in modo informale da Sir Isaac Newton nel 1665.

Molti altri importanti matematici hanno affrontato il teorema binomiale dopo Newton. Era un problema molto allettante nei secoli XVII e XVIII.

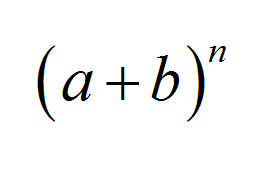
La formula per l'espansione binomiale

Ciò che è intero nel teorema binomiale è che fornisce una formula molto elegante e concisa. Prima di entrare nella formula, facciamo alcuni calcoli. Ad esempio, per $n = 2$ otteniamo:

\large (a+b)^2 = (a+b) \times (a+b) = a(a+b) + b(a+b) = a^2 + ba + ab + b^2

\large = a^2 + 2ab + b^2

Ora proviamo con $n = 3$ :

\large (a+b)^3 = (a+b)^2 \times (a+b) = (a^2 + 2ab+b^2)(a+b)

\large = a^3 + 2a^2b + ab^2 + a^2b + 2ab^2 + b^3

\large = a^3 + 3a^2b + 3ab^2 + b^3

Infine, siamo coraggiosi e provalo con $n = 4$ :

\large (a+b)^4 = (a+b)^3 \times (a+b) = (a^3 + 3a^2b + 3ab^2 + b^3)(a+b)

\large = a^4 + 3a^3 b + 3a^2b^2 + ab^3 + a^3b + 3a^2b^2 + 3ab^3 + b^4

\large = a^4 + 4a^3b + 6 a^2 b^2 + 4a b^3 + b^4

Ok, è stato coraggioso, eh ?? Vedi degli schemi lì. Posso vederne alcuni. Ad esempio, per $n = 2$ potremmo semplificarlo in 3 termini. Per $n = 3$ potremmo semplificarlo a 4 termini e per $n = 4$ potremmo semplificarlo a 5 termini. Quindi, in generale, mi aspetto che per la potenza generale di $n$ , avremo termini $n+1$

Più modelli? Bene, c'è sempre un termine nella forma $a^l b^m$ , e possiamo vedere che i poteri $l$ diminuiscono e i poteri $m$ aumentano. Ma c'è anche qualcosa di interessante: se controlli ogni termine, la somma dei poteri è sempre $n$ . Infatti, controllerai che $l + m = n$ per tutti quei termini.

Ad esempio, per $n = 2$ hai il termine $2 a b$ . La potenza di $a$ è 1 e la potenza di $b$ è 1 e la somma delle potenze è $1 + 1 = 2$ . O ad esempio, per $n = 4$ hai il termine $6 a^2 b^2$ , dove la potenza di $a$ è 2 e la potenza di $b$ è 2 e la somma dei poteri è $2 + 2 = 4$

Il teorema binomiale generale

Ora siamo pronti a dare l'espressione generale per il teorema binomiale. Pronto? Abbiamo:

\large (a+b)^n = a^n + {n \choose 1} a^{n-1} b + {n \choose 2} a^{n-2} b^2 + ... + {n \choose n-1} a b^{n-1} + b^n

dove il termine ${n \choose i}$ si legge come "n scegli i" o anche come "coefficiente combinatorio", ed è definito come

\large \displaystyle {n \choose i}= \frac{n!}{i! \times (n-i)!}

Per esempio,

\large \displaystyle {5 \choose 2} = \frac{5!}{2! \times (5-2)!} = \frac{5!}{2! \times 3!} = \frac{120}{2 \times 6} = 10

Puoi usare questo calcolatore del coefficiente combinatorio per saperne di più e per esercitarti vedendo tutti i passaggi mostrati.

Il teorema binomiale generale utilizzando una somma

La somma sopra che definisce il teorema binomiale usa la notazione per estensione, per rendere i termini più comprensibili. Come sempre in matematica, cerchiamo di rendere le cose più compatte e l'espressione sopra può essere riassunta come:

\large \displaystyle (a+b)^n = \sum_{i=0}^n {n \choose i} a^i b^{n-i}

Osserva i poteri dei termini nell'espansione. Il termine generale è $a^i b^{n-i}$ (moltiplicato per una costante). La somma dei poteri è $i + (n-i) = n$ . Quindi la somma delle potenze di TUTTI i termini nell'espansione deve essere $n$ . Non è carino ???

ESEMPIO 1

Il termine $x^3 y^2$ (moltiplicato per una costante) può essere parte dell'espansione di $(x+y)^6$ ? Perché?

RISPOSTA:

La risposta è no. In questo caso, $n = 6$ , e sappiamo dal teorema binomiale che la somma delle potenze dei termini $x^l y^m$ nell'espansione deve essere uguale a $n$ . In questo caso, $l + m = 3 + 2 = 5$ , che non è uguale a $n = 6$ . Quindi, il termine $x^3 y^2$ (moltiplicato per una costante) non può far parte dell'espansione di $(x+y)^6$ .

ESEMPIO 2

Espandi $(a-b)^3$ utilizzando il teorema binomiale.

RISPOSTA:

Aspettare. Stai pensando "Mi hai appena insegnato come espandere $(a+b)^n$ , ma ora mi chiedi di $(a-b)^n$ . Perché sei così crudele". Resisti. Non ti sto giocando brutti scherzi.

C'è sempre un trucco (non dimenticare quella linea, appare molto in matematica).

Osserva che $a - b$ è uguale a $a + (-b)$ .

Ahhhhhhh, quindi il teorema binomiale si applica ancora. Allora:

\large (a-b)^3 = (a+(-b))^3 = a^3 + {3 \choose 1} a^2 (-b) + {3 \choose 2} a (-b)^2 + (-b)^3

\large \displaystyle = a^3 - \frac{3!}{1! \times 2!} a^2 b + \frac{3!}{2! \times 1!} a b^2 -b^3

\large \displaystyle = a^3 - \frac{6}{1 \times 2} a^2 b + \frac{6}{2 \times 1} a b^2 -b^3

\large = a^3 - 3 a^2 b + 3 a b^2 -b^3

Ulteriori informazioni sull'espansione binomiale

Il teorema binomiale è così importante che è trattato principalmente in tutti i corsi, inclusi Algebra, Calcolo, Probabilità e Statistica.

Ci sono alcune generalizzazioni come l'espansione binomiale negativa, che va oltre lo scopo di questo tutorial.

Il triangolo Pascal

A volte gli studenti si bloccano quando devono calcolare le costanti (i coefficienti combinatori) che entrano nell'espansione binomiale. Un modo davvero semplice per farlo è usare il triangolo Pascal.

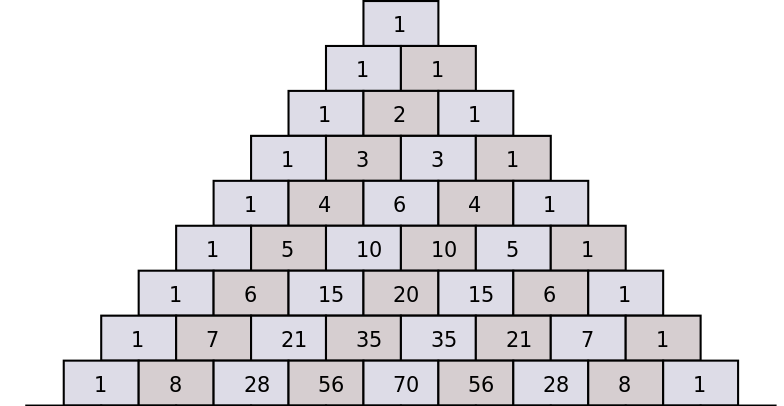
Il triangolo Pascal mostra come i coefficienti binomiali successivi possono essere calcolati in base ai coefficienti del valore precedente di $n$ , sommando i due coefficienti che vengono immediatamente sopra.

Applicazioni

L'espansione binomiale ha molteplici applicazioni in Algebra e nella Teoria della Probabilità. Ad esempio, in Probability, la distribuzione binomiale è basata sul teorema binomiale.

Infatti, considera un numero $0 \le p \le 1$ . Quindi, $p + (1-p) = 1$ e possiamo usare il teorema binomiale:

\large \displaystyle 1 = 1^n = (p + (1-p))^n = \sum_{i=0}^n {n \choose i} p^i (1-p)^{n-i}

che significa che

\large \displaystyle \sum_{i=0}^n {n \choose i} p^i (1-p)^{n-i} = 1

Risulta che ciascuno dei termini ${n \choose i} p^i (1-p)^{n-i}$ rappresenta una probabilità. Inoltre, abbiamo:

\large \Pr(X = i) = {n \choose i} p^i (1-p)^{n-i} = 1

dove $X$ è il numero di successi dopo $n$ prove, quando la probabilità di successo di ciascuna prova è $p$ . La variabile $X$ è nota come variabile casuale binomiale.