Equazioni letterali
Le equazioni letterali sono equazioni in cui sono presenti simboli che non sono variabili, ma rappresentano una costante. Quindi è come un'equazione, ma alcuni dei numeri invece di essere numeri sono espressi come costanti generiche.
In questo tutorial imparerai come gestire le equazioni letterali e come operare con esse.
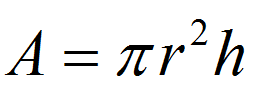
Cos'è un'equazione letterale
Il primo compito da svolgere è specificare cos'è un'equazione letterale. Quando diciamo "letterale", ci riferiamo a "lettere". Sì, dal latino letterale deriva da "lettere"
Quindi, un'equazione letterale è un'equazione che coinvolge molte "lettere", invece di numeri. Quelle lettere non dovrebbero essere variabili, dovrebbero rappresentare numeri, in termini di costante generica.
Pertanto, per identificare un'equazione letterale, dobbiamo vedere molte lettere, di cui una (o potenzialmente più) è l'effettiva
variabile
.
Come in qualsiasi altra equazione, l'idea è di risolvere per la variabile (che significa isolare la variabile su un lato dell'equazione).
Ad esempio, considera la formula per il volume di un cilindro di raggio \(r\) e altezza \(h\):
\[V = \pi r^2 h\]Questa è un'equazione letterale. Perché? Perché abbiamo un'equazione con molte lettere.
La domanda è qual è la variabile e quali sono le costanti. In verità, questo è soggettivo, in una certa misura.
Ad esempio, si potrebbe sostenere che \(V\) è la variabile e \(r\) e \(h\) sono i valori letterali (o costanti) e avrebbe senso.
Ma si potrebbe dire che, ad esempio, ci vengono dati il volume \(V\) e l'altezza \(h\) e devi trovare il raggio \(r\). In tal caso abbiamo la stessa equazione letterale, ma la variabile sarebbe \(r\).
È importante sapere qual è la variabile in un'equazione letterale, per sapere per cosa stiamo risolvendo.
Strategie per gestire un'equazione letterale
Quindi, abbiamo un'equazione letterale, e adesso? Ebbene, come ogni altra equazione, dovremmo cercare di risolverla.
Ciò significa che dobbiamo isolare la variabile su un lato dell'equazione e mettere tutto il resto, utilizzando tutte le regole algebriche disponibili, sull'altro lato.
Ciò significa, in termini pratici, che stiamo esprimendo la variabile in termini (o come funzione) delle costanti (letterali).
Il processo di risoluzione delle equazioni letterali è lo stesso di quello per risolvere le equazioni regolari:
Aggiungiamo, sottraiamo, moltiplichiamo o dividiamo i termini su entrambi i lati dell'uguaglianza per isolare la variabile.
Non c'è un modo per risolvere, dipende dalle caratteristiche e dalla struttura dell'equazione.
Esempi di risoluzione di equazioni letterali
Il modo più veloce per apprendere un'abilità in matematica è PRATICARE. Eccoci qui.
ESEMPIO 1:
Torniamo all'esempio del cilindro. Per un cilindro con un dato volume \(V\) e altezza \(h\), trova il suo raggio \(r\)
RISPOSTA:
Sappiamo che la formula per il volume di un cilindro è
\[\large V = \pi r^2 h\]Per l'equazione letterale sopra, abbiamo che la variabile (quella per cui vogliamo risolvere) è \(r\) e le costanti (valori forniti) sono \(V\) e \(h\).
Il processo di risoluzione per \(r\) è mostrato di seguito:
\[\large V = \pi r^2 h\] \[\large \displaystyle \Rightarrow \frac{V}{\pi h} = r^2\] \[\large \displaystyle \Rightarrow \sqrt{\frac{V}{\pi h}} = r\]Pertanto, l'equazione letterale è risolta, perché abbiamo \(r\) isolato su un lato dell'uguaglianza e il resto sull'altro.
ESEMPIO 2:
Risolvi la seguente equazione letterale:
\[\large m n = \frac{x-y}{k} \]per \(x\).
RISPOSTA:
In questo caso ci viene detto esplicitamente che la variabile è \(x\), quindi tutte le altre lettere sono costanti ai fini della risoluzione dell'equazione.
Quando si risolve per \(x\) si ottiene quanto segue:
\[\large m n = \displaystyle \frac{x-y}{k} \] \[\large m n k = x-y \] \[\large m n k+y = x \]che termina il calcolo.
Ulteriori informazioni sulla risoluzione di equazioni letterali
Perché facciamo un fuzz sulla differenza tra equazioni letterali ed equazioni regolari? In realtà, non facciamo una peluria. Un'equazione letterale è un'equazione, prima di tutto.
L'esercizio concettuale consiste nel rendersi conto che indipendentemente dal fatto che abbiamo un numero o una costante che rappresenta un numero generico, il processo di risoluzione dell'equazione è identico. Questo è il concetto chiave.
Come risolvere equazioni letterali con frazioni
Quindi cosa succede se trovi le frazioni quando risolvi un'equazione letterale con le frazioni? Ebbene, lo stesso che faresti con un'equazione regolare: se vuoi eliminare qualcosa che è nel denominatore, moltiplica entrambi i lati dell'equazione per esso, e se vuoi eliminare qualcosa che è nel numeratore, dividi entrambi i lati dell'equazione da esso.
C'è qualche strategia che funziona meglio?
Non proprio. A seconda del tipo di equazione che hai, potresti utilizzare alcune strategie specifiche per semplificare il tuo lavoro. Ad esempio, se hai un file equazione logaritmica (un'equazione in cui la variabile è all'interno di un logaritmo), è meglio fare un uso efficiente del regole di registro per risolvere queste equazioni in modo efficiente.