Come trovare la portata
Imparare a trovare l'intervallo di una funzione può rivelarsi molto importante in Algebra e Calcolo, perché ti dà la capacità di valutare quali valori vengono raggiunti da una funzione. O in altre parole, ti permette di trovare l'insieme di tutte le immagini tramite la funzione
Il compito di trovare quali punti possono essere raggiunti da una funzione è molto utile. Ad esempio, potresti avere una funzione di produzione \(q(x)\), che ti fornisce la quantità di output ottenuta per \(x\) unità di input.
Vorremmo sapere quante unità di input sono necessarie per produrre \(b\) unità di output. Quindi, in altre parole, dobbiamo trovare \(x\) in modo che \(q(x) = b\), che è un altro modo per chiedere se \(b\) è o meno nell'intervallo della funzione \(q(x)\).
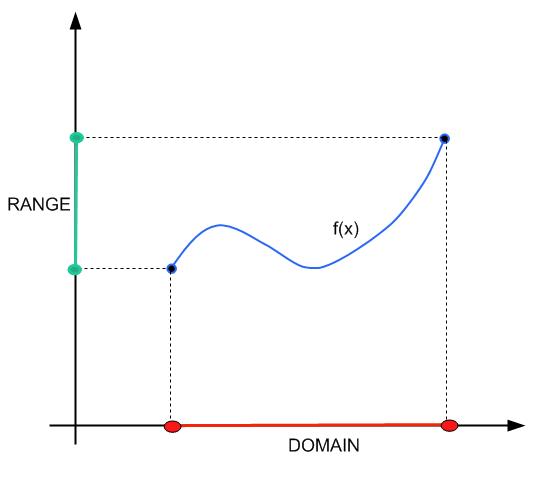
In questo tutorial ci concentreremo maggiormente sui meccanismi per trovare la portata. Per un approccio più concettuale al dominio e alla portata, puoi farlo controlla questo tutorial .
Il modo algebrico di trovare la portata di una funzione
Come quando abbiamo imparato a calcolare il dominio, non esiste una ricetta per trovare l'intervallo, dipende davvero dalla struttura della funzione \(f(x)\).
Tuttavia, esiste una tecnica algebrica che verrà sempre utilizzata. Questo è il modo in cui trovi la gamma. Fai attenzione:
Supponiamo che dobbiamo ottenere l'intervallo di una determinata funzione \(f(x)\). Quindi, considereremo un numero reale generico \(y\) e proveremo a risolvere per \(x\) la seguente equazione:
\[f(x) = y\]Dobbiamo determinare per quali valori di \(y\) l'equazione precedente può essere risolta per \(x\). Questo è tutto. Ovviamente, potrebbe essere difficile da fare, a seconda della struttura della funzione \(f(x)\), ma è quello che devi fare.
Quindi questo è il modo algebrico, il modo in cui trovare l'intervallo di una funzione senza rappresentare graficamente.
ESEMPIO 1
Trova l'intervallo della funzione \(\displaystyle f(x) = \frac{x+1}{x-3}\):
RISPOSTA:
Procediamo in modo algebrico: sia \(y\) un numero e risolveremo \(x\) nella seguente equazione: \(f(x) = y\). Il valore \(y\) è compreso nell'intervallo se \(f(x) = y\) può essere risolto per \(x\).
In questo caso abbiamo:
\[\large f(x) = y \Leftrightarrow \frac{x+1}{x-3} = y\] \[\Rightarrow \,\,\,x+1 = y\left( x-3 \right)\] \[\Rightarrow \,\,\,x+1 = yx-3y\] \[\Rightarrow \,\,\,x-yx=-1-3y\] \[\Rightarrow \,\,\,x\left( 1-y \right)=-1-3y\] \[\Rightarrow \,\,\,x=\frac{3y+1}{y-1}\]Quindi, quando \(x\) sarà ben definito? Quasi per tutti \(y\), tranne quando \(y = 1\), perché in quel caso abbiamo una divisione per \(0\). Quindi, l'intervallo di \(f\) in questo caso è l'intera linea reale, tranne 1.
Se usiamo la notazione dell'intervallo, possiamo scrivere \(Range(f) = (-\infty, 1) \cup (1, +\infty)\).
ESEMPIO 2
Trova l'intervallo della funzione \(f(x) = x^2 - 4x + 3\):
RISPOSTA:
Ancora una volta, procediamo usando il modo algebrico, quindi conosci il trapano: Sia \(y\) un numero e risolveremo per \(x\) nella seguente equazione: \(f(x) = y\). Il valore \(y\) è compreso nell'intervallo se \(f(x) = y\) può essere risolto per \(x\).
In questo caso abbiamo:
\[\large f(x) = y \Leftrightarrow x^2 - 4x + 3 = y\] \[\Rightarrow \,\,\, x^2 - 4x + 3 - y = 0 \text{ (This is a quadratic equation in x)}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{-(-4) \pm \sqrt{(-4)^2 - 4(1)(3-y)}}{2(1)}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{16 - 4(3-y)}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{16 - 12 + 4y}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = \frac{4 \pm \sqrt{4 + 4y}}{2}\] \[\Rightarrow \displaystyle \,\,\, x = 2 \pm \sqrt{1+y}\]Ora, vedendo questa espressione finale, quando sarà ben definito \(x\)? Dobbiamo avere che l'argomento della radice quadrata deve essere non negativo, quindi abbiamo bisogno di:
\[1+y \ge 0\]il che significa che \(y \ge -1\). Se usiamo la notazione dell'intervallo, possiamo scrivere \(Range(f) = [-1, +\infty)\).
In questo esempio, avremmo potuto risolverlo utilizzando il fatto che \(f(x) = x^2 - 4x + 3\) è una funzione quadratica e il suo grafico è una parabola che si apre verso l'alto.
Il punto minimo di questa parabola viene raggiunto al vertice. La coordinata x del vertice è:
\[\displaystyle x_V = \frac{-b}{2a} =\frac{-(-4)}{2(1)} =\frac{4}{2} = 2\]Ora, la coordinata y del vertice si trova semplicemente inserendo il valore \(x_V = 2\) nella funzione quadratica:
\[y_V = f(x_V) = 2^2 - 4(2) + 3 = -1\]Poiché il valore minimo raggiunto dalla parabola è \(-1\), concludiamo che l'intervallo è \([-1, +\infty)\), che è la stessa conclusione di quello trovato algebricamente.
Il grafico della funzione \(f(x) = x^2 - 4x + 3\) lo rende ancora più chiaro:
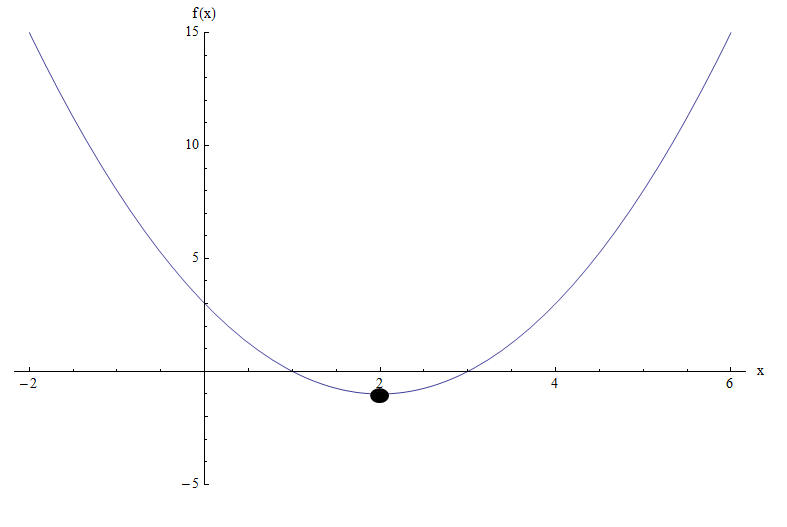
Possiamo vedere che, in base al grafico, il minimo viene raggiunto in \(x = 2\), che è esattamente ciò che è stato trovato alla coordinata x del vertice.
Il rischio di utilizzare il grafico per trovare l'intervallo è che potresti potenzialmente interpretare erroneamente i punti critici nel grafico e fornire una valutazione imprecisa del punto in cui la funzione raggiunge il suo massimo o minimo.
Altre strategie per trovare l'intervallo di una funzione
Come abbiamo visto nell'esempio precedente, a volte possiamo trovare l'intervallo di una funzione semplicemente osservando il suo grafico.
Ad esempio, supponi di voler trovare l'intervallo della funzione \(f(x) = x + 3\). Il grafico è mostrato di seguito:
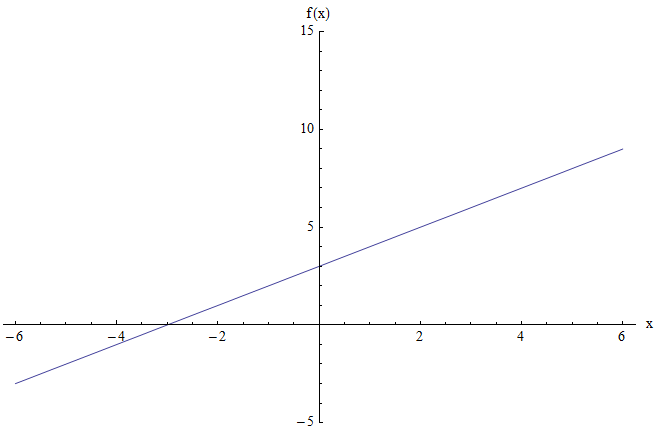
Il grafico sopra non mostra alcun punteggio minimo o massimo. Inoltre, quando \(x\) è grande e positivo, anche il valore della funzione è grande e positivo. E analogamente, quando \(x\) è molto negativo, anche il valore della funzione è molto negativo.
L'intuizione è che la funzione può assumere valori negativi e positivi quanto vogliamo, selezionando valori \(x\) abbastanza grandi (positivi o negativi). E poi, la conclusione è che l'intervallo è l'intera linea reale, che è \((-\infty, +\infty)\) usando la notazione dell'intervallo.
Tale analisi è corretta in termini di risultato, ma è fragile in termini di ragionamento. Il "metodo grafico" per trovare la gamma ha questo problema: è accattivante dal punto di vista intuitivo, ma è piuttosto scarno in termini di contenuto.
Normalmente, se possibile, dovremmo preferire la via analitica / algebrica. Nell'esempio, dobbiamo risolvere per \(x\):
\[x + 3 = y\] \[\Rightarrow \,\, x = y - 3\]Quindi, c'è qualche restrizione su \(y\) affinché \(x\) sia ben definito? Niente affatto, quindi non ci sono restrizioni su \(y\) e la conclusione è che l'intervallo è l'intera linea reale.
Puoi controllare questo articolo che desideri sapere come trovare il dominio di una funzione anziché.
Ci sono molte buone ragioni algebriche per trovare l'intervallo, una di queste è perché fa parte dei processi per trovare l'inverso di una funzione .
