Praticando Estatística Descritiva
A melhor maneira de aprender a resolver problemas de Estatística Descritiva de maneira adequada é PRATICAR. Aqui você tem alguns exemplos passo a passo, exclusivamente para nossos assinantes
Questão 1: A HiEd realizou 5 visitas de recrutamento na região este ano. O número de alunos do último ano do ensino médio que participam desses eventos é fornecido abaixo.
10 15 20 35 20
O número médio de alunos do último ano do ensino médio participando de um evento é 20.
uma. Determine o intervalo para esta amostra.
b. Determine o desvio padrão.
Solução: (a) O intervalo é calculado como:
\[Range=Max-Min = {35}-{10} = {25}\]
(b) Finalmente, a seguinte tabela mostra os cálculos necessários para calcular o desvio padrão:
|
X |
X² |
|
|
10 |
100 |
|
|
15 |
225 |
|
|
20 |
400 |
|
|
35 |
12: 25h |
|
|
20 |
400 |
|
|
Soma = |
100 |
2350 |
A variação da amostra é
\[{{s}^{2}}=\frac{1}{n-1}\left( \sum{X_{i}^{2}}-\frac{{{\left( \sum{{{X}_{i}}} \right)}^{2}}}{n} \right)=\frac{1}{5-1}\left( 2350-\frac{{{\left( 100 \right)}^{2}}}{5} \right)=87.5\]e também descobrimos que o desvio padrão é calculado como
\[s=\sqrt{87.5}=9.3541\]
,p> Question 2: The Financial Times/Harris poll is a monthly online poll of adults from six countries in Europe and the united states. The poll conducted in January 2008 included 1015 adults. One of the questions asked was "How would you rate the federal bank in handling the credit problems in the financial markets?" Possible responses were excellent, good, fair, bad, and terrible. The 1015 responses for this question can be found in the data file named fedbank.uma. Construa uma distribuição de frequência.
b. Construa uma distribuição de frequência percentual.
c. Construa um gráfico de barras para a distribuição de frequência percentual.
d. Comente como os adultos nos Estados Unidos acham que o banco federal está lidando com os problemas de crédito nos mercados financeiros.
e. Na Espanha, foi perguntado a 1.114 adultos: “Como você classificaria o banco central europeu no tratamento dos problemas de crédito nos mercados financeiros?” A distribuição de frequência percentual obtida é a seguinte.
Frequência percentual de classificação
excelente 0
bom 4
justo 46
40 ruins
terrível 10
Compare os resultados obtidos na Espanha com os resultados obtidos nos Estados Unidos.
Solução: (a) O seguinte é obtido:
|
Avaliação |
Frequência |
|
Mau |
244 |
|
Excelente |
20 |
|
Justo |
528 |
|
Boa |
101 |
|
Terrível |
122 |
|
Total geral |
1015 |
(b) Agora temos:
|
Avaliação |
Frequência |
Frequência percentual |
|
Mau |
244 |
24,04% |
|
Excelente |
20 |
1,97% |
|
Justo |
528 |
52,02% |
|
Boa |
101 |
9,95% |
|
Terrível |
122 |
12,02% |
|
Total geral |
1015 |
100,00% |
(c) O seguinte é obtido:
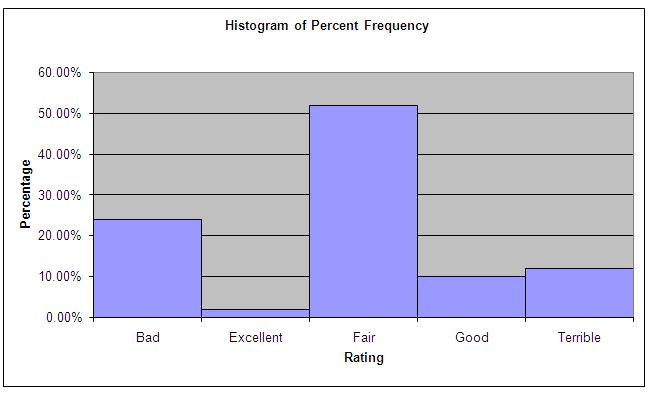
(d) Em grande maioria, os adultos norte-americanos acham que o alimento está sendo tratado de maneira justa.
(e) Em Espanha, a maioria dos adultos pensa que o tratamento é justo e mau.
Questão 3: Para o seguinte conjunto de pontuações:
3, 7, 6, 5, 5, 9, 6, 4, 6, 8, 10, 2, 7, 4, 9, 5, 6, 3, 8
uma. Construa uma tabela de distribuição de frequência.
b. Esboce um polígono mostrando a distribuição.
c. Descreva a distribuição usando as seguintes características:
(1) Qual é a forma da distribuição?
(2) Qual pontuação melhor identifica o centro (média) para a distribuição?
(3) As pontuações estão agrupadas ou estão espalhadas pela escala?
Solução: (a) Os valores mínimo e máximo obtidos a partir dos dados fornecidos são
Min = 2
Máx = 10
Com base nisso, escolhemos a classe mais baixa para ser 2. A largura mínima da classe é (10 - 2) / 5 = 1,6, então escolhemos uma largura da classe de 2. Portanto, os respectivos limites inferiores da classe são calculados como Li = 2 + 2 * i. A tabela a seguir mostra a tabela de frequência:
|
Aulas |
Frequência |
Rel. Frequência |
Frequência acumulativa |
Rel. Frequência acumulativa |
|
2 - 3 |
3 |
0,158 |
3 |
0,158 |
|
4 - 5 |
5 |
0,263 |
8 |
0,421 |
|
6 - 7 |
6 |
0,316 |
14 |
0,737 |
|
8 - 9 |
4 |
0,211 |
18 |
0,947 |
|
10-11 |
1 |
0,053 |
19 |
1 |
O seguinte histograma é obtido
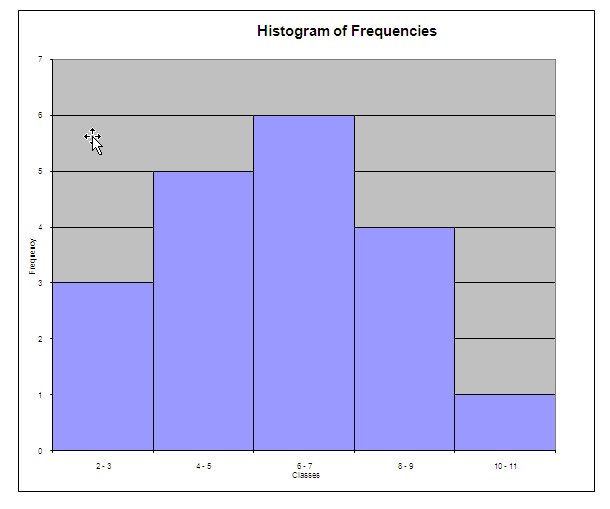
(b) O seguinte polígono de frequência é obtido
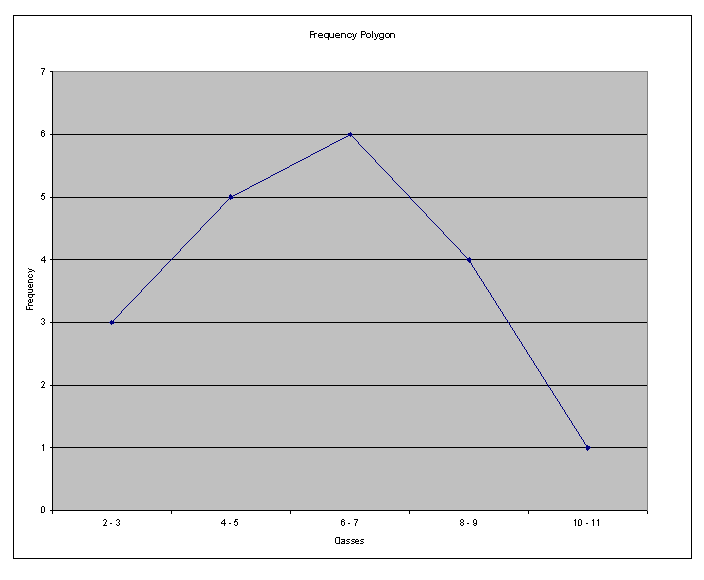
(c) (1) A distribuição é aproximadamente simétrica.
(2) Como a distribuição é aproximadamente simétrica, a média seria a melhor medida de tendência central.
(3) As pontuações estão relativamente espalhadas pela escala, embora estejam um pouco concentradas no centro.
