Saiba mais sobre este fabricante de P-Chart.

Esta calculadora de gráfico P é uma ferramenta gráfica muito utilizada para avaliar se um processo está em controlo estatístico, geralmente analisando o comportamento da proporção de defeito da amostra em muitas amostras.

A grande vantagem de utilizar uma ferramenta gráfica é que se pode facilmente encontrar padrões e identificar pontos que parecem desviar-se de um comportamento "normal", ou mais precisamente, o que seria de esperar sob certas suposições distributivas comuns.

Como posso utilizar esta calculadora de gráficos P online?

A ideia é que tenha uma lista de \(N\) amostras, e para cada amostra tem um número de defectivos e o tamanho da amostra. Normalmente o tamanho da amostra é o mesmo para todas as amostras, mas nem sempre é o caso.

Depois, para cada amostra, calculará a proporção de amostra de defectivos \(\p_i\)>>. Em geral, teremos \(N\) proporção de amostra de defectivos, uma para cada amostra. Finalmente, encontra-se a média da proporção de defectivos, a que se chama \(\bar{p}\)>.

Depois de ter tudo isso, pode utilizar as seguintes fórmulas para obter os limites inferior e superior de controlo para o gráfico p

\[ LCL_{p} =\bar{p} - 3\sqrt{\frac{\bar{p}(1-\bar{p})}{k}} \] \[ UCL_{p} =\bar{p} + 3\sqrt{\frac{\bar{p}(1-\bar{p})}{k}} \]>

onde \(k\) é o tamanho de amostra comum de TODAS as amostras com que se está a trabalhar.

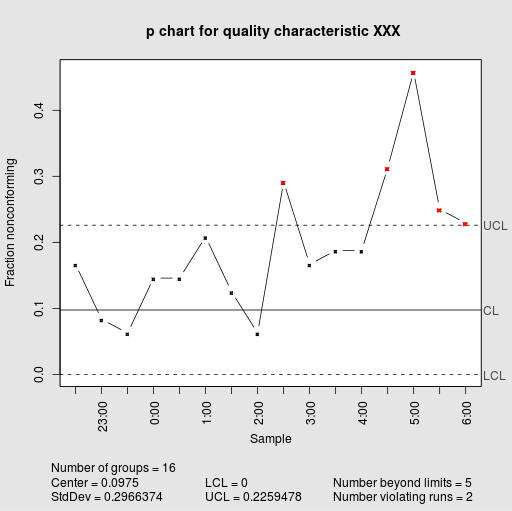
Resumindo: Como se faz um P-chart?

Passo 1. A primeira coisa a fazer é recolher os dados que pretende medir, neste caso, os defectivos, porque está interessado em analisar a proporção de defectivos em última análise.

Passo 2. Agora, para cada amostra é calculada a proporção de amostra de defectivos (que é, número de defectivos dividido pelo tamanho da amostra) .

Passo 3. O passo seguinte é calcular a média de todas as amostras de defectivos.

Passo 4. Depois é necessário utilizar as fórmulas para os limites de controlo inferior e superior \(LCL_{p} =\bar{p} - 3\sqrt{\frac{\bar{p}(1-\bar{p})}{k}}\) e \(UCL_{p} =\bar{p} + 3\sqrt{\frac{\bar{p}(1-\bar{p})}{k}} \)>>.

Passo 5. Agora constrói-se um gráfico onde se traça a proporção de defectivos para cada amostra, sob a forma de uma parcela de linha, e também é necessário traçar os limites inferior e superior, bem como a linha central.

Passo 6. Na etapa final, determina-se se qualquer proporção de defectivos vai ou não além de qualquer dos limites de controlo.

Os pontos que ultrapassam os limites de controlo inferior e superior, caso existam, são considerados fora de controlo estatístico, e também o processo não se encontra em controlo estatístico. Quando nenhum ponto está fora de controlo estatístico, então dizemos que o processo está em controlo estatístico.

Outro gráfico de controlo

Poderá estar interessado em utilizar um Gráfico R para avaliar se a variabilidade do processo está ou não sob controlo. Além disso, se precisar de avaliar se o centro do processo está ou não em controlo estatístico, pode utilizar este X-bar Chart Maker .