Un sistema di equazioni è semplicemente un insieme di due o più equazioni simultanee che devono essere risolte. In genere, avrai lo stesso numero di equazioni e incognite (variabili), ma non deve essere così.

L'unica cosa chiara è che per avere un sistema di equazioni è necessario avere DUE o PIÙ equazioni simultanee. Ad esempio, il sistema seguente

è un sistema di equazioni, con due equazioni e due incognite (\(x\) e \(y\)). O ad esempio, il sistema seguente:

è un sistema di equazioni, con due equazioni e tre incognite (\(x\), \(y\) e \(z\)).

Il primo esempio è un esempio di un sistema di equazioni lineari.

Il secondo esempio è un esempio di un sistema di equazioni non lineari. Perché? Hai indovinato: il termine \(z^2\) nella prima equazione lo rende non lineare.

In termini generali, la strategia utilizzata per risolvere un sistema di equazioni dipende dal fatto che sia lineare o meno. Per i sistemi lineari di equazioni, esistono metodi sistematici per risolverli, come Regola di Cramer . Per i sistemi di equazioni non lineari, non esiste una strategia fissa e dobbiamo procedere caso per caso.

Numero di soluzioni di un sistema di equazioni

Quante soluzioni ha un sistema di equazioni, se ce ne sono? Una risposta generale a questa domanda può essere data solo nel caso di sistemi di equazioni lineari, in base alla relazione tra il numero di equazioni e il numero di incognite.

Tipicamente, in un sistema di equazioni lineari in cui il numero di equazioni è uguale o maggiore del numero di incognite, potrebbe esserci una soluzione unica, nessuna soluzione o infinite soluzioni.

Quando il numero di equazioni è inferiore al numero di incognite, potrebbe esserci un numero infinito di soluzioni o nessuna soluzione, ma non potrebbe esserci un'unica soluzione.

Come trovi un sistema di equazioni?

Questa domanda è collegata a come si fa a trovare un sistema di equazioni. Esistono diversi contesti. Ad esempio, potresti avere a che fare con un problema di parole, in cui stai producendo tre diversi tipi di alimenti e hai diversi tipi di restrizioni su quegli alimenti in termini di costo, calorie, ecc. Ciascuna di queste restrizioni può probabilmente essere rappresentato come un'equazione.

Esistono innumerevoli applicazioni in cui differenti restrizioni portano a equazioni lineari che devono essere risolte simultaneamente, convertendo il problema in un sistema di equazioni.

ESEMPIO 1

Esempio di sistema di equazioni: È il seguente sistema di equazioni lineare o non lineare?

RISPOSTA:

Prima di tutto, quanto sopra è un sistema di equazioni, con tre equazioni e tre incognite (\(x\), \(y\) e \(z\)). Le prime due equazioni sono lineari indipendentemente dal fatto che l'ultima equazione sia non lineare, a causa del termine \(\sin(z)\). Per avere un'equazione lineare, dobbiamo moltiplicare le incognite solo per una costante.

Quindi, il sistema di equazioni di cui sopra non è lineare, anche se le prime due equazioni sono lineari, la terza non lo è. Per un sistema, è sufficiente avere un'equazione per non essere lineare perché l'intero sistema sia non lineare.

ESEMPIO 2

Supponi di produrre tre tipi di camicie nelle seguenti quantità: \(x\), \(y\) e \(z\). Il tipo 1 ha un costo di $ 1, il tipo 2 un costo di $ 1,2 e il tipo 3 un costo di $ 1,5. Inoltre, ci vuole 1 ora per produrre il tipo 1, 0,5 ore per produrre il tipo 2 e 0,8 ore per il tipo di prodotto 3.

So di avere 800 dollari da spendere e 500 ore a disposizione. Inoltre, in base alle stime della mia domanda, desidero produrre un totale di camicie di tipo 1 che sia l'equazione del totale combinato di tipo 2 e tipo 3.

Scrivi un sistema di equazioni basato su queste restrizioni. Questo sistema è lineare?

RISPOSTA:

Si noti che ci sono tre incognite (\(x\), \(y\) e \(z\)), che corrispondono al numero di camicie di ogni tipo che devono essere prodotte. Inoltre, abbiamo tre equazioni: una per il costo, una per il numero di ore disponibili e una per la restrizione del numero di camicie di tipo 1 e gli altri tipi.

Le seguenti equazioni rappresentano la situazione:

Usando la convenzione di lasciare tutti i termini che dipendono dalle incognite sul lato sinistro, riscriviamo l'ultima equazione per ottenere:

Si noti che ogni equazione è lineare, quindi il sistema è un sistema di equazioni lineari.

Come risolvete i sistemi di uguaglianza in generale?

Come accennato in precedenza, non esiste un'unica strategia adatta a tutti i casi. Solo nel caso di sistemi di equazioni lineari ci sarà una strategia chiara e ben definita.

Tuttavia, ci sono alcune buone pratiche o passaggi che devi seguire che possono aiutarti a risolvere tutti i tipi di sistemi di equazioni:

Passo 1: Identifica ogni equazione nel sistema

Passo 2: Spostare su un lato dell'equazione tutti i termini che dipendono dalle incognite (tipicamente sul lato sinistro) e le costanti sull'altro lato

Passaggio 3: Semplifica sia il lato sinistro (con le incognite) che il lato destro (con le costanti)

Passaggio 4: Identifica la struttura delle equazioni. Le equazioni sono lineari o non lineari?

Passaggio 5: Se tutte le equazioni sono lineari, utilizza uno dei metodi sistematici per risolvere i sistemi lineari (regola di Cramer, sostituzione, eliminazione, riduzione di Gauss, ecc.)

Passaggio 6: Se almeno un'equazione è non lineare, puoi provare a utilizzare l'approccio della sostituzione, iniziando dall'equazione più semplice.

Ulteriori informazioni sui sistemi di equazioni

Il sistema di equazioni appare ovunque in matematica, in tutte le materie. Essere in grado di risolvere sistematicamente sistemi di equazioni si rivelerà un'abilità cruciale da padroneggiare.

Il sistema più tipico che troverai è un sistema di equazioni lineari. E spesso troverai sistemi di equazioni lineari, con due equazioni e due incognite. Questi sistemi sono generalmente chiamati sistema 2x2 di equazioni lineari.

Rappresentazione grafica del sistema di equazioni

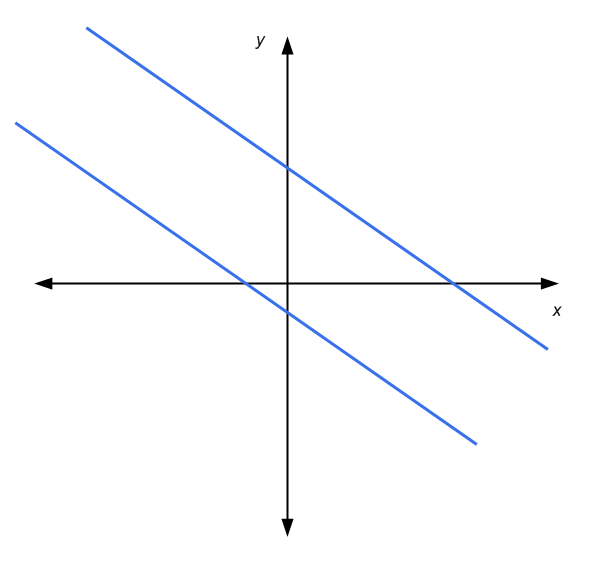
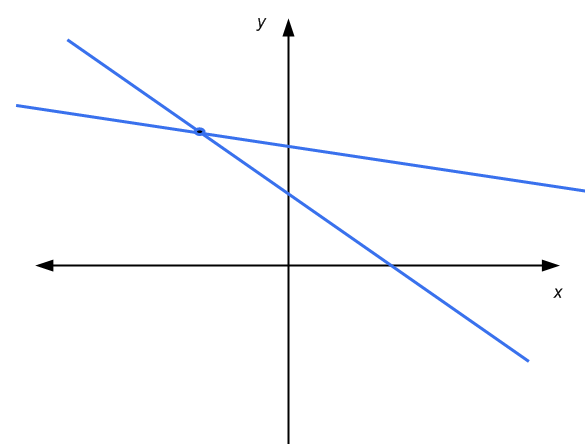
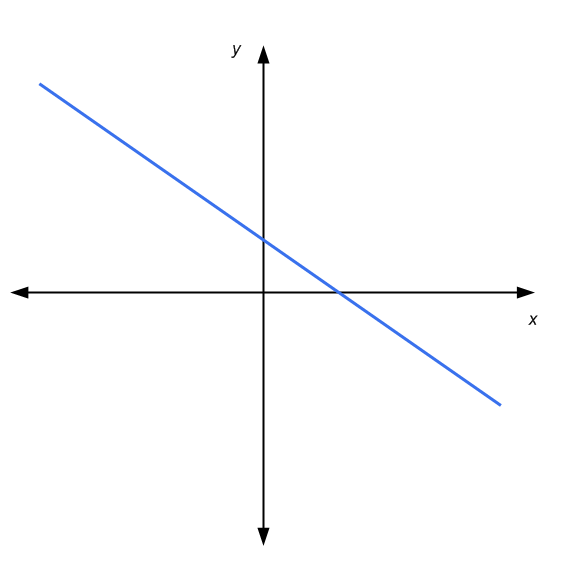
Per il sistema 2x2 di equazioni lineari, abbiamo il vantaggio di poter utilizzare una rappresentazione grafica negli assi coordinati. Un'equazione lineare è rappresentata da una linea nel piano x-y. Graficamente, la soluzione di un sistema 2x2 è il punto in cui le due linee si intersecano, se presenti.

Quindi, in questo caso abbiamo o: le linee sono parallele e non si toccano (nessuna soluzione), le linee si intersecano in un punto (soluzione unica), oppure le linee sono parallele e si toccano (infinite soluzioni )

Calcolatore del sistema di equazioni

Usa questo risolutore se vuoi risolvere un sistema 2x2 di equazioni lineari . Questa calcolatrice utilizza la regola di Cramer per risolvere i sistemi 2x2. Per sistemi di equazioni più grandi, la migliore alternativa è usare il Metodo di eliminazione gaussiana , che si occupa sistematicamente di sistemi lineari di qualsiasi dimensione.