Regola di Cramer
La regola di Cramer è una tecnica utilizzata per risolvere sistematicamente sistemi di equazioni lineari, basati sui calcoli dei determinanti.
Tipicamente, risolvendo sistemi di equazioni lineari può essere complicato per i sistemi più grandi di 2x2, perché ci sono molti modi per aggirare il problema quando ci sono tre o più variabili.
La regola di Cramer fornisce un modo inequivocabile e sistematico per trovare soluzioni a sistemi di equazioni lineari, indipendentemente dalle dimensioni del sistema.
Il numero di calcoli richiesti aumenta per i sistemi di grandi dimensioni, ma la procedura è esattamente la stessa, indipendentemente dalle dimensioni del sistema.
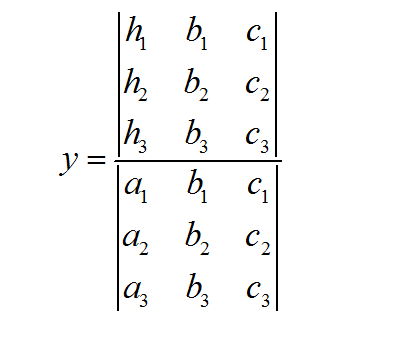
Come usare la regola di Cramer
Per rendere le cose più facili, elaboreremo il caso per \(n = 2\) e poi stabiliremo una versione più generale che, si spera, avrà più senso dopo aver affrontato il caso \(n=2\).
Passo 1
: Tutti i sistemi lineari 2x2 possono essere scritti nella seguente forma:
Quindi il tuo primo passo è trovare questi valori \(a_1, b_1, c_1\) e \(a_2, b_2, c_2\) per il sistema che vuoi risolvere.
Passo 2
: Dopo aver ottenuto i coefficienti \(a_1, b_1, c_1\) e \(a_2, b_2, c_2\), utilizzare le seguenti formule per risolvere \(x\) e \(y\):
Nella formula sopra, dove si dice "det", significa il determinante della matrice corrispondente. A volte, per i determinanti viene utilizzata una notazione più compatta, come mostrato di seguito:
\[\large \displaystyle \det \left[\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right] = \left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right| \]Quindi, usando la notazione sopra, otterremmo queste formule più compatte per la regola di Cramer:
\[\large \displaystyle x = \frac{ \left|\begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \] \[\large \displaystyle y = \frac{ \left|\begin{matrix} a_1 & c_1 \\ a_2 & c_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \]Cerchiamo di avere un modo visivo per capire cosa sta succedendo. Osserva che sia \(x\) che \(y\) hanno lo stesso determinante nel denominatore.
I coefficienti di quella matrice comune usata nel denominatore derivano direttamente dai coefficienti che moltiplicano \(x\) e \(y\) nel sistema. Guarda l'immagine qui sotto:
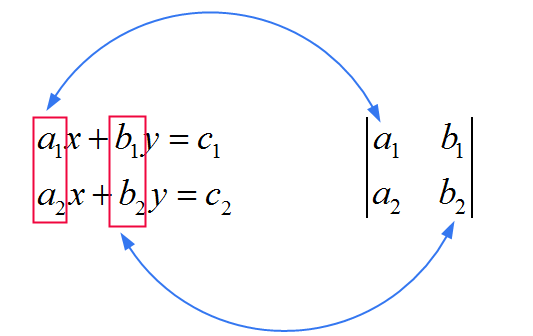
Ora vediamo che \(x\) e \(y\) differiscono per ciò che hanno al numeratore. Come modo per ricordare la regola, pensa a questo:
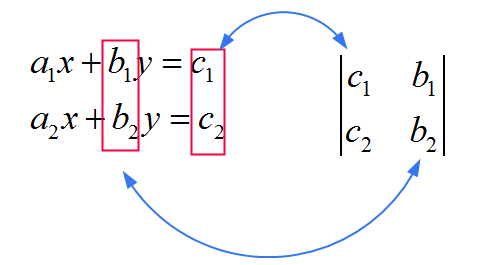
Per \(x\), usi la matrice STESSA come quella nel denominatore, solo che sostituisci la PRIMA colonna con i coefficienti \(c_1\) e \(c_2\). Vedi l'immagine sotto
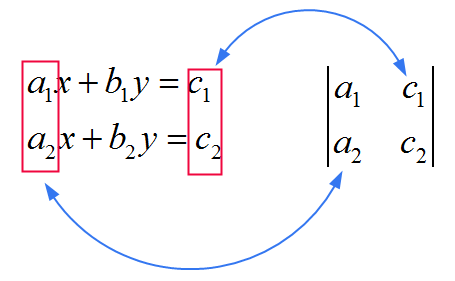
Per \(y\), usi la matrice STESSA come quella nel denominatore, solo che sostituisci la SECONDA colonna con i coefficienti \(c_1\) e \(c_2\). Vedi l'immagine sotto
ESEMPIO 1
Risolvi il seguente sistema lineare 2x2:
\[\large 2x + 8y = 10\] \[\large 2x - 4y = 4\]RISPOSTA:
Seguiamo i due passaggi che abbiamo delineato sopra per utilizzare la regola di Cramer per risolvere il sistema sopra:
Passo 1
: Dobbiamo identificare i coefficienti per i determinanti corrispondenti.
Per la matrice che va nel denominatore usiamo
\[ \left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right| = \left|\begin{matrix} 2 & 8 \\ 2 & -4 \end{matrix}\right| \]Ora, in questo caso \(c_1 = 10, c_2 = 4\), per il determinante utilizzato per calcolare \(x\), sostituiamo la matrice precedente cambiando la PRIMA colonna:
\[ \left|\begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}\right| = \left|\begin{matrix} 10 & 8 \\ 4 & -4 \end{matrix}\right| \]Per il determinante utilizzato per calcolare \(y\) sostituiamo la matrice precedente cambiando la SECONDA colonna:
\[ \left|\begin{matrix} a_1 & c_1 \\ a_2 & c_2 \end{matrix}\right| = \left|\begin{matrix} 2 & 10 \\ 2 & 4 \end{matrix}\right| \]Quindi ora otteniamo la soluzione:
\[\large \displaystyle x = \frac{ \left|\begin{matrix} c_1 & b_1 \\ c_2 & b_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \] \[ = \frac{\left|\begin{matrix} 10 & 8 \\ 4 & -4 \end{matrix}\right|}{\left|\begin{matrix} 2 & 8 \\ 2 & -4 \end{matrix}\right|} = \frac{10 \times (-4) - 4\times 8}{2 \times (-4) - 2 \times 8} = \frac{-72}{-24} = 3 \]e per \(y\):
\[\large \displaystyle y = \frac{ \left|\begin{matrix} a_1 & c_1 \\ a_2 & c_2 \end{matrix}\right| }{\left|\begin{matrix} a_1 & b_1 \\ a_2 & b_2 \end{matrix}\right|} \] \[ = \frac{\left|\begin{matrix} 2 & 10 \\ 2 & 4 \end{matrix}\right|}{\left|\begin{matrix} 2 & 8 \\ 2 & -4 \end{matrix}\right|} = \frac{2 \times 4 - 2\times 10}{2 \times (-4) - 2 \times 8} = \frac{-12}{-24} = \frac{1}{2} \]Pertanto, la soluzione è \(x = 3\), \(y = 1/2\).
Regola di Cramer per il caso generale
La bellezza della regola di Cramer è che applica esattamente la stessa procedura, sia che si tratti di un sistema 2x2 che di un sistema 10x10. Il concetto è lo stesso.
Quindi, supponiamo che \(x_1, x_2, ..., x_n\) siano le variabili (le incognite) e vogliamo risolvere il seguente sistema n x n di equazioni lineari:
\[\large a_{11} x_1 + a_{12} x_2 + .... + a_{1n} x_n = c_1 \] \[\large a_{21} x_1 + a_{22} x_2 + .... + a_{2n} x_n = c_2 \] \[\large \vdots \] \[\large a_{n1} x_1 + a_{n2} x_2 + .... + a_{nn} x_n = c_n \]Per risolvere per \(x_1, x_2, ..., x_n\), useremo il seguente determinante sul denominatore:
\[\large\displaystyle \left|\begin{matrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & a_{nn}\end{matrix}\right|\]• La soluzione per \(x_1\) è
\[\large\displaystyle x_1 = \frac{ \left|\begin{matrix} c_1 & a_{12} & ... & a_{1n} \\ c_2 & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ c_n & a_{n2} & ... & a_{nn}\end{matrix}\right| }{\left|\begin{matrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & a_{nn}\end{matrix}\right|} \]• La soluzione per \(x_2\) è
\[\large\displaystyle x_1 = \frac{ \left|\begin{matrix} a_{11} & c_1 & ... & a_{1n} \\ a_{21} & c_2 & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & c_n \end{matrix}\right| }{\left|\begin{matrix} a_{11} & a_{12} & ... & a_{1n} \\ a_{21} & a_{22} & ... & a_{2n} \\ \vdots & \vdots & ... & \vdots\\ a_{n1} & a_{n2} & ... & a_{nn}\end{matrix}\right|} \]E così via. Come puoi vedere, il determinante nel denominatore è lo stesso e quello nel numeratore si ottiene cambiando la prima colonna con \((c_1, ..., c_n)\) per \(x_1\). Per \(x_2\) cambiamo la seconda colonna di \((c_1, ..., c_n)\), per \(x_3\) cambiamo la terza colonna e così via. Hai avuto l'idea.
ESEMPIO 2
Risolvi il seguente sistema di equazioni lineari 3x3 usando la regola di Cramer.
\[\large x_1 + x_2 + x3 = 20\] \[\large x_1 - x_2 + x3 = 4\] \[\large 2x_1 + x_2 - x3 = 16\]RISPOSTA:
Innanzitutto, identifichiamo il determinante che va nel denominatore:
\[\large\displaystyle \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right|\]Inoltre, dobbiamo identificare il vettore dei coefficienti \(c_i\):
\[\large\displaystyle \left[\begin{matrix} 20 \\ 4 \\ 16 \end{matrix}\right]\]Questo vettore sarà quello che sostituirà le colonne corrispondenti del determinante comune dal denominatore. Noi abbiamo:
\[\large\displaystyle x_1 = \frac{ \left|\begin{matrix} 20 & 1 & 1 \\ 4 & -1 & 1 \\ 16 & 1 & -1 \end{matrix}\right| }{ \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right| } = \frac{40}{6} = \frac{20}{3}\] \[\large\displaystyle x_2 = \frac{ \left|\begin{matrix} 1 & 20 & 1 \\ 1 & 4 & 1 \\ 2 & 16 & -1 \end{matrix}\right| }{ \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right| } = \frac{40}{6} = \frac{20}{3}\] \[\large\displaystyle x_3 = \frac{ \left|\begin{matrix} 1 & 1 & 20 \\ 1 & -1 & 4 \\ 2 & 1 & 16 \end{matrix}\right| }{ \left|\begin{matrix} 1 & 1 & 1 \\ 1 & -1 & 1 \\ 2 & 1 & -1 \end{matrix}\right| } = \frac{40}{6} = \frac{20}{3}\]Ulteriori informazioni sulla regola di Cramer
La regola di Cramer ha un ruolo specifico nella risoluzione efficiente di sistemi di equazioni lineari. Implica l'uso di determinanti per rendere molto semplice un compito che altrimenti sarebbe davvero complicato, soprattutto per sistemi più grandi.
In definitiva, al fine di risolvere sistemi lineari , tutto ciò che devi fare è identificare i determinanti della matrice numerica in base al sistema che deve essere risolto e condurre una semplice operazione algebrica per risolvere il sistema.
Applicazioni
La regola di Cramer ha molte applicazioni sia in algebra lineare che in equazioni differenziali.