Formula di elasticità dell'arco per una tabella

La formula dell'elasticità d'arco della domanda consente di stimare l'elasticità nei punti indicati in una tabella di programmazione della domanda, senza disporre di una formula esplicita per la funzione di domanda.

Ciò che devi fornire è una tabella con una colonna per il prezzo e una colonna per la quantità richiesta. Una volta digitata o incollata nel foglio di calcolo fornito, cliccherai su "Calcola" per ottenere le corrispondenti elasticità d'arco calcolate per te.

Si noti che questa è solo un'approssimazione: la situazione ideale è quella di calcolare le elasticità utilizzando la funzione di domanda , utilizzando i derivati.

Passaggi per l'utilizzo dell'elasticità dell'arco per una tabella

Il formula di elasticità dell'arco È:

\[ \varepsilon_{ARC} = \displaystyle \left(\frac{Q_2 - Q_1}{P_2 - P_1}\right) \left(\frac{P_1 + P_2}{Q_1 + Q_2}\right)\]

e questo può essere applicato a punti consecutivi in una tabella di programmazione della domanda. Seguirai questi passaggi:

• Passo 1: Tabulare correttamente i valori per il prezzo (P) e la quantità domandata (Q)
• Passo 2: Puoi creare colonne per Q2 - Q1, P2 - P1, Q1 + Q2 e P1 + P2 se vuoi rendere i calcoli più chiari, oppure puoi calcolare la formula direttamente
• Passaggio 3: Ci sarà un punto saltato nella tabella, poiché l'elasticità dell'arco prende un punto sulla tabella e il punto che segue immediatamente nella tabella

Utilizzando questa approssimazione dell'elasticità d'arco si otterrà un quadro eccellente della sensibilità alle variazioni di prezzo per il bene specifico analizzato, anche se si tratta solo di un'approssimazione.

Più punti di domanda abbiamo, migliore sarà l'approssimazione, soprattutto se quei punti di prezzo sono ravvicinati.

Cosa misura l'elasticità dell'arco?

L'elasticità dell'arco mira a fornire un'approssimazione della vera elasticità in un dato punto. L'elasticità effettiva dalla curva di domanda è calcolata da:

\[ \varepsilon = \displaystyle \frac{dQ}{dP} \cdot \frac{P}{Q}\]

Si potrebbe sostenere che l'elasticità dell'arco è solo un'approssimazione, quindi come mai ha un valore? La risposta a ciò è che per l'analisi dell'elasticità, e per l'analisi di sensibilità in Economia in generale, siamo più interessati agli intervalli che a punti molto specifici.

In effetti, ai fini della microeconomia, è utile sapere se ci troviamo in un intervallo anelastico o meno, piuttosto che il valore molto specifico dell'elasticità

Non che il valore specifico non sia importante, anzi è sicuramente un bene averlo, ma le elasticità d'arco sono spesso una buona approssimazione e ci forniranno rappresentazioni molto precise del tipo di intervallo di elasticità che stiamo affrontando.

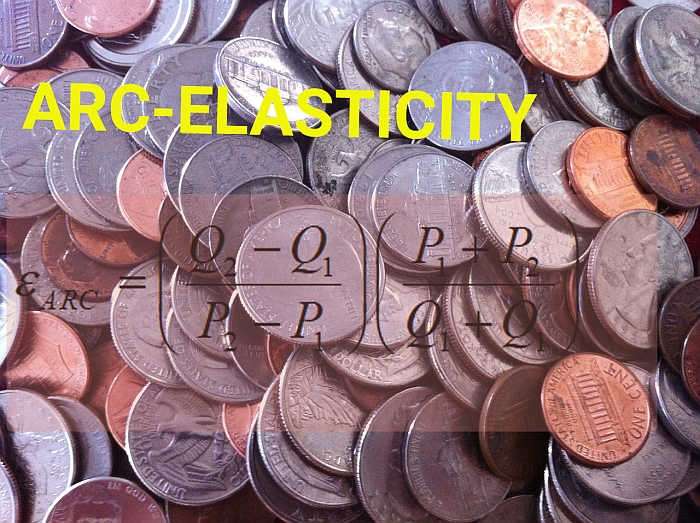
Esempio

Si consideri la seguente tabella della domanda con informazioni sul prezzo e sulla quantità domandata

Fornire l'approssimazione dell'elasticità dell'arco per i punti dati in questa tabella.

P	Q
1	200
1.5	190
2	170
2.5	155
3	130
3.5	110
4	90
4.5	60

Soluzione: Per approssimare l'elasticità della domanda rispetto al prezzo da questi dati, dobbiamo utilizzare la seguente formula di elasticità dell'arco

\[ \varepsilon_{ARC} = \displaystyle \left(\frac{Q_2 - Q1}{P2_P1}\right)\left(\frac{P_1 + P_2}{Q_1 + Q_2}\right)\]

Applicando la formula sopra a tutte le coppie di punti dati consecutivi, troviamo le seguenti elasticità d'arco:

P	Q	Elasticità Dell'Arco
1	200	-
1.5	190	\(\left(\frac{ 190 - 200}{ 1.5 - 1}\right) \left(\frac{ 1 + 1.5}{ 200 + 190}\right) = -0.13\)
2	170	\(\left(\frac{ 170 - 190}{ 2 - 1.5}\right) \left(\frac{ 1.5 + 2}{ 190 + 170}\right) = -0.39\)
2.5	155	\(\left(\frac{ 155 - 170}{ 2.5 - 2}\right) \left(\frac{ 2 + 2.5}{ 170 + 155}\right) = -0.42\)
3	130	\(\left(\frac{ 130 - 155}{ 3 - 2.5}\right) \left(\frac{ 2.5 + 3}{ 155 + 130}\right) = -0.96\)
3.5	110	\(\left(\frac{ 110 - 130}{ 3.5 - 3}\right) \left(\frac{ 3 + 3.5}{ 130 + 110}\right) = -1.08\)
4	90	\(\left(\frac{ 90 - 110}{ 4 - 3.5}\right) \left(\frac{ 3.5 + 4}{ 110 + 90}\right) = -1.5\)
4.5	60	\(\left(\frac{ 60 - 90}{ 4.5 - 4}\right) \left(\frac{ 4 + 4.5}{ 90 + 60}\right) = -3.4\)

Interpretazione

La tabella trovata mostra l'elasticità approssimativa del prezzo della domanda per ciascuno dei punti di prezzo forniti. Questi valori possono essere approssimativamente utilizzati per determinare intervalli elastici e anelastici per la tabella di domanda fornita.

Altri calcolatori economici

Se lavori in econometria, questo Calcolatrice di regressione sarà probabilmente utile, soprattutto perché mostra tutti i passaggi del processo di calcolo dei coefficienti di regressione .

Puoi anche usare un equazione logaritmica per stimare un curva di domanda con elasticità costante .