Asintoti orizzontali
In questo tutorial tratteremo il concetto di asintoto orizzontale e le sue applicazioni più importanti. Cercheremo di evitare spiegazioni eccessivamente tecniche, ma verranno utilizzati alcuni tocchi di Calcolo.
Principalmente, la parte importante che si ottiene da questo tutorial è una forte intuizione geometrica sugli asintoti orizzontali. Cominciamo!
Cos'è un asintoto orizzontale
Un asintoto orizzontale è un limite superiore, che puoi immaginare come una linea orizzontale che stabilisce un limite per il comportamento del grafico di una determinata funzione.
Ciò significa che il grafico della funzione \(f(x)\) si avvicina a questa linea orizzontale, man mano che aumenta il valore di \(x\).
Come si trova l'asintoto orizzontale?
Comprendere questo comportamento orizzontale limitante delle funzioni che presentano questa caratteristica può rivelarsi molto utile per trovare asintoti orizzontali.
In effetti, in determinate circostanze, questo comportamento limitante assomiglia molto a quello di una linea orizzontale per grandi valori di \(x\). Vedi ad esempio la funzione qui sotto.
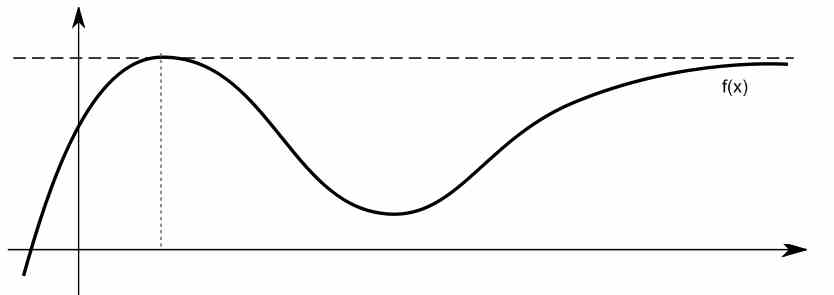
Come si trova l'asintoto orizzontale di una funzione utilizzando i limiti?
Per rendere più chiara la definizione, una linea orizzontale \(y = h\) è un asintoto orizzontale della funzione \(f(x)\) se
\[\large \lim_{x\to\infty} f(x) = h\]se il limite di cui sopra esiste ed è finito. Per coloro che non hanno ancora seguito un corso di calcolo, la linea orizzontale \(y = h\) è un asintoto orizzontale della funzione \(f(x)\) quando \(h\) è la limite di \(f(x)\) man mano che \(x\) si avvicina all'infinito. Cosa significa essere un “limite”? Ciò significa che per valori sufficientemente grandi di \(x\), il valore di \(f(x)\) sarà tanto vicino a \(h\) quanto predeterminato. Fantasia, vero?
Qual è la formula dell'asintoto orizzontale?
Per trovare la formula dell'asintoto orizzontale, dobbiamo prima trovare il limite corrispondente. Supponiamo di averlo fatto
\[\large \lim_{x\to\infty} f(x) = h\]In tal caso, diremo che l'asintoto orizzontale è \(h\) e la formula per l'asintoto orizzontale è \(y = h\). In altre parole, l'asintoto orizzontale è semplice è la linea orizzontale, questa è una linea con pendenza zero.
Ciò dà il significato a cosa significa un asintoto orizzontale in termini di limiti: il limite trovato corrisponde a definire la linea orizzontale che viene chiamata asintoto orizzontale.
Esempio 1
Trova un asintoto orizzontale per la funzione
\[ \large f(x) = \frac{x^2}{x^2+1} \]Risposta:
Per trovare l'asintoto orizzontale, dobbiamo trovare il limite della funzione \(f(x)\) quando \(x\) si avvicina all'infinito. Se non hai familiarità con il calcolo infinitesimale, dovresti prima provare a valutare la funzione con un valore molto grande di \(x\).
Ad esempio, diciamo che \(x = 1,000,000\). Inseriamo questo numero nella funzione:
\[ \large f(1,000,000) = \frac{1,000,000^2}{1,000,000^2+1} = \frac{1,000,000,000,000}{1,000,000,000,000+1}\] \[ = \frac{1,000,000,000,000}{1,000,000,000,001} = 0.999999999999 \]che è maledettamente vicino a 1. Allora si dovrebbe sospettare che il limite sia 1. Infatti, risulta che quando \(x\) è grande, il valore di \(x^2\) è così grande rispetto a 1, che \(x^2\) è molto simile a \(x^2 + 1\) almeno in termini relativi. Quindi abbiamo, dividendo numeratore e denominatore per \(x^2\):
\[ \large f(x) = \frac{x^2}{x^2+1} = \frac{1}{1+\frac{1}{x^2}} \rightarrow \frac{1}{1+0} = 1 \]perché \(\frac{1}{x^2}\) si avvicina a 0 mentre \(x\) si avvicina all'infinito. Pertanto, non è difficile dimostrarlo o esserne convinti
\[\large \lim_{x\to\infty} f(x) =\large \lim_{x\to\infty} \frac{x^2}{x^2+1} = 1\]il che significa che l'asintoto orizzontale è \(y = 1\). Ora, fai attenzione alla risposta se stai rispondendo a un test o a un compito a casa. Alcune persone diranno "l'asintoto orizzontale è 1", il che è sbagliato.
Tecnicamente, l'asintoto orizzontale è la funzione \(y = 1\) e NON il numero 1. L'asintoto orizzontale è una funzione costante, che non è la stessa cosa di un numero. Lo dico solo perché ci sono alcuni selezionatori esigenti là fuori.
Esempio 2
Trova un asintoto orizzontale, se esiste per la funzione
\[ \large f(x) = \frac{x^3}{x^2+1} \]Risposta:
Dividendo numeratore e denominatore per \(x^2\):
\[ \large f(x) = \frac{x}{1+\frac{1}{x^2}} \]Ma aspetta! Il trucco non ha funzionato qui? Sì, l'ha fatto. Nota che il denominatore diventerà molto vicino a 1 man mano che \(x\) diventa molto grande, e il numeratore diventerà molto grande.
Non è difficile credere che \(f(x)\) converga all'infinito, per cui non esiste un asintoto orizzontale. Ogni volta che vediamo una funzione illimitata, come nel caso di \(f(x)\) in questo esempio, non avremo un asintoto orizzontale.
Asintoto orizzontale o asintoti orizzontali?
Tecnicamente potrebbero esserci due asintoti orizzontali, uno a sinistra e uno a destra. L'asintoto orizzontale sinistro è \(y = h_L\) se
\[\large \lim_{x \to -\infty} f(x) = h_L\]Allo stesso modo, l'asintoto orizzontale destro è \(y = h_R\) se
\[\large \lim_{x \to +\infty} f(x) = h_R\]nel caso in cui uno qualsiasi dei limiti di cui sopra esista e sia finito. Può succedere che una funzione abbia due asintoti orizzontali, abbia un solo asintoto orizzontale o non ne abbia nessuno.
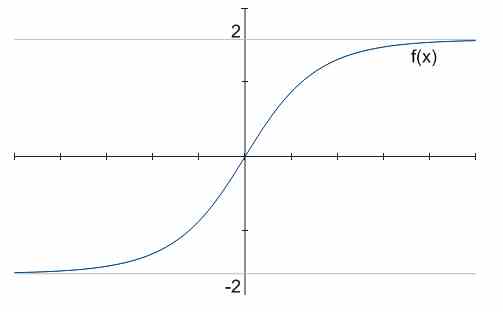
Ad esempio, nel grafico sopra ci sono due asintoti orizzontali, \(y = -2\) e \(y = 2\).
Qual è la regola per trovare l'asintoto orizzontale?
Non esistono regole generali che valgano per tutti i casi. Nel caso generale dobbiamo calcolare il limite quando \(x\) si avvicina a \(-\infty\), e il limite quando \(x\) si avvicina a \(+\infty\).
Se uno qualsiasi di questi limiti esiste e è finito, avremo gli asintoti orizzontali.
Si può elaborare una regola specifica nel caso in cui la data funzione \(f(x)\) sia il quoziente di due polinomi. In tal caso, assumiamo che \(m\) sia l'ordine del polinomio al numeratore e \(n\) sia l'ordine del polinomio al denominatore. Allora abbiamo i seguenti casi:
Caso 1: Se \(m < n\), l'asintoto orizzontale è \(y = 0\).
Caso 2: Se \(m = n\) e \(a\) è il coefficiente principale del polinomio al numeratore e \(b\) è il coefficiente principale del polinomio al denominatore, allora l'asintoto orizzontale è \(\displaystyle y = \frac{a}{b}\).
Caso 3: Se \(m > n\), allora non esiste un asintoto orizzontale.
Esempio 2
Trova, se esiste, l'asintoto orizzontale della funzione
\[\large f(x) = \frac{3x^2+2x-1}{2x^2 -x+2}\]Risposta:
La funzione è costituita dal quoziente di due polinomi. Il polinomio al numeratore è \(3x^2+2x-1\), che è un polinomio di ordine 2, quindi \(m = 2\), e coefficienti iniziali 3.
Il polinomio al denominatore è \(2x^2 -x+2\), che è un polinomio di ordine 2, quindi allora \(n = 2\) e costante iniziale 2. Puoi usare il nostro Calcolatrice polinomiale per condurre questa divisione mostrando tutti i passaggi.
Quindi, poiché in questo caso \(m = n\), c'è un asintoto orizzontale, ed è il quoziente dei coefficienti principali, quindi in questo caso l'asintoto orizzontale è
\[\large y = \frac{3}{2}\]Ulteriori informazioni sugli asintoti orizzontali
Quindi la tua domanda è come trovare gli asintoti di un'equazione, giusto? Innanzitutto trovi gli asintoti di a funzione , non di un'equazione. Quindi è necessario iniziare con la definizione generale, utilizzando i limiti.
Se non conosci il calcolo infinitesimale e non sai come calcolare i limiti, dovresti almeno provare a inserire valori molto grandi di \(x\) e anche valori molto negativi di \(x\) nella funzione, e vedere come la funzione si comporta
Anche tracciare la funzione con alcuni software può darti un chiaro suggerimento se sono presenti asintoti orizzontali.
In definitiva, nel caso molto ristretto in cui la funzione è a quoziente di polinomi , quindi puoi applicare la regola in base agli ordini \(m\) e \(n\).
Come trovare asintoti orizzontali con gradi diversi?
Questi sono diversi tipi di asintoti e sono chiamati asintoto obliquo. Parleremo degli asintoti obliqui in un altro tutorial.
