وظائف عقلانية

ستسمح لك حاسبة الدالة الكسرية هذه بتحليل النقاط الأكثر صلة بالدالة الكسرية التي تقدمها, مع جميع الخطوات الموضحة. عادةً, بالنسبة لمعظم الوظائف العقلانية, يمكنك العثور على التقاطعات والخطوط المقاربة الرأسية ورسمها البياني. بعض الدوال العقلانية المحددة سيكون لها أيضًا خطوط مقاربة أفقية.

نوع الوظيفة التي يمكنك توفيرها هو مثل 'f(x)=1/x - x', أو شيء يتضمن متعددات الحدود بدرجة أعلى مثل 'f(x) = (x^3-1)/(x^2+x )'

بمجرد توفير دالة عقلانية صالحة, يمكنك النقر فوق زر الحساب, وستحصل على جميع الخطوات الموضحة لك.

إحدى السمات الرئيسية للدالة العقلانية هي أنه يمكنك في الغالب تقليل العملية الحسابية إلى مشكلة حل المعادلات متعددة الحدود , وهو أحد "أبسط" أنواع معادلات يمكنك حلها .

ما هي الوظيفة العقلانية

الوظيفة العقلانية هي وظيفة تتضمن حاصل اثنين من كثيرات الحدود \(P(x)\) و \(Q(x)\), حيث المقسوم عليه \(Q(x)\) لا يساوي صفر متعدد الحدود. إذن, صيغة الدالة الكسرية هي

\[\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} \]

على سبيل المثال, الدالة

\[\displaystyle f(x) = \displaystyle \frac{x^2-1}{x+1} \]

هي دالة عقلانية, لأنها بالضبط حاصل قسمة كثيرتي الحدود. لكن على سبيل المثال

\[\displaystyle g(x) = \displaystyle \frac{x^2+1}{\sin x} \]

ليست عقلانية لأن المقسوم عليه ليس كثير الحدود. لاحظ أنه عندما نقول أن المقسوم عليه \(Q(x)\) لا يساوي الصفر متعدد الحدود, فإننا لا نقول أن \(Q(x)\) لا يمكن أن يحتوي على أصفار. على سبيل المثال, في حالة \(\displaystyle f(x) = \displaystyle \frac{x^2-1}{x+1} \), يكون المقسوم عليه \(Q(x) = x + 1\), والذي يحتوي على صفر واحد, عند \(x = -1\).

ما لا نريده هو شيء من هذا القبيل

\[\displaystyle g(x) = \displaystyle \frac{x^2+1}{0} \]

لأنه على الرغم من أن \(Q(x) = 0\) في هذه الحالة متعدد الحدود من الناحية الفنية, إلا أنه متعدد الحدود صفر (وهو صفر في كل مكان).

خطوات حساب دالة عقلانية

• الخطوة 1: أولاً, تأكد من أن لديك دالة كسرية, حيث يمكنك تحديد البسط P(x) والمقام Q(x)
• الخطوة 2: إذا لم تجد بدقة الهيكل الموصوف أعلاه, عليك التوقف. قد تحتاج إلى تجميع المصطلحات معًا عبر التخفيضات الجبرية .
• الخطوه 3: أنت بحاجة إلى العثور على الأصفار الحقيقية لـ P(x) وQ(x), إن وجدت. ستكون الاستنتاجات التي تم العثور عليها مرتبطة ارتباطًا وثيقًا بأصفار كل من P(x) وQ(x)
• الخطوة 4: للعثور على تقاطع y, يمكنك تقييم الدالة عند الصفر, عن طريق حساب f(0). سيتم تعريف التقاطع y جيدًا إذا كانت x = 0 ليست صفرًا لـ Q(x)
• الخطوة 5: للعثور على تقاطعات x, تحصل على أصفار P(x) التي ليست أصفار Q(x)
• الخطوة 6: للعثور على الخطوط المقاربة الرأسية, تحتاج إلى العثور على أصفار Q(x) التي ليست أصفار P(x)
• الخطوة 7: للعثور على الخطوط المقاربة الأفقية, يجب أن تكون درجة Q(x) أكبر من أو تساوي الدرجة P(x)

لاحظ أنه كما هو متوقع, يعتمد تحليل دالة عقلانية على العثور على أصفار من كثير الحدود , ومن ثم تجميع كل الاستنتاجات معًا. .

لاحظ أن مجال الدالة الكسرية هو الخط الحقيقي بأكمله باستثناء أصفار المقسوم عليه Q(x). إذا كان هناك صفر لـ Q(x) وهو أيضًا صفر لـ P(x), فيمكن إصلاح الانقطاع. يعتمد مدى الدالة العقلانية على درجات P(x) وQ(x).

لماذا استخدام الوظائف العقلانية

يتم استخدام الدوال المنطقية لأنها امتدادات طبيعية لمتعددات الحدود. يمكن للمرء أن ينظر إليها على أنها الخطوة التالية في تعقيد الوظيفة. كما نعرف, تعبيرات كثيرات الحدود هي من بين أبسط الوظائف التي يمكن أن نجدها, ولكنها مع ذلك من بين الوظائف الأكثر فائدة أيضًا.

عادة ما تظهر المعادلات المنطقية في مسائل الخلط الأكثر تقدمًا, ومع ذلك, من السهل التعامل معها بشكل مدهش, بشرط أن تكون كثيرات الحدود المعنية بسيطة بما فيه الكفاية. نعلم كيفية حل المعادلات التربيعية , ولكن بالنسبة لمتعددات الحدود من الدرجة 3 وما فوقها, يمكن أن تكون الأشياء أكثر تعقيدًا.

هي وظائف كثيرة الحدود أيضا وظائف عقلانية

نعم, إذا كانت P(x) كثيرة الحدود, فإن P(x) عقلانية أيضًا, لأننا نستطيع أن نكتب:

\[\displaystyle f(x) = \displaystyle \frac{P(x)}{1} \]

وQ(x) = 1 هي كثيرة حدود فعلية. والعكس غير صحيح: فالدالة العقلانية ليست بالضرورة متعددة الحدود. لماذا هذا؟ لأنه بطبيعة الحال, ما لم يكن Q(x) = 1, عندما يكون لديك \(\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} \), فلن يكون لديك أن جميع المصطلحات ستكون مصطلحات مجانية كما هو مطلوب في تعريف كثير الحدود.

وبشكل أكثر رسمية, باستخدام نظرية الباقي , لدينا

\[\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} = d(x) + \frac{r(x)}{Q(x)}\]

حيث \(d(x)\) هي كثيرة الحدود, ولكن \frac{r(x)}{Q(x)} ليست كذلك, لأن درجة r(x) أقل من درجة Q(x).

مثال: العمل مع الوظائف العقلانية

ابحث عن التقاطعات والخطوط المقاربة والرسم البياني لـ: \(f(x) = \frac{x^2-1}{x+1}\)

حل:

لقد تم تزويدنا بالوظيفة التالية:

\[f\left(x\right)=\frac{x^2-1}{x+1}\]

نحن بحاجة إلى العثور على الاعتراضات والخطوط المقاربة, إن وجدت. بعد ذلك, سيتم عرض الرسم البياني للوظيفة.

دعونا نجد أصفار الدالة المحددة. نحن بحاجة إلى حل المعادلة العقلانية التالية:

\[\frac{x^2-1}{x+1}=0\]

لاحظ أنه بالنسبة لـ \(x \ne -1\) يمكننا التبسيط على النحو التالي:

\[\frac{x^2-1}{x+1} = 0 \Rightarrow \frac{(x-1)(x+1)}{x+1} = 0 \Rightarrow x-1 = 0\]

معادلة البسط المساعدة

والآن نجعل البسط يساوي صفرًا ونوجد الحلول. إذن, تلك الجذور التي لا تجعل المقام يساوي صفرًا ستكون حلولاً للمعادلة النسبية.

يجب حل ما يلي لإيجاد جذور البسط: \(x^2-1=0\)

للمعادلة التربيعية للنموذج \(a x^2 + bx + c = 0\), يتم حساب الجذور باستخدام الصيغة التالية:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

في هذه الحالة , لدينا أن المعادلة التي نحتاج إلى حلها هي \(\displaystyle x^2-1 = 0\), مما يعني أن المعاملات المقابلة هي:

\[a = 1\] \[b = 0\] \[c = -1\]

أولاً , سنحسب التمييز لتقييم طبيعة الجذور.يتم حساب التمييز على النحو التالي:

\[\Delta = b^2 - 4ac = \displaystyle \left( 0\right)^2 - 4 \cdot \left(1\right)\cdot \left(-1\right) = 4\]

لأنه في هذه الحالة , نحصل على التمييز هو \(\Delta = \displaystyle 4 > 0\), وهو أمر إيجابي , نعلم أن المعادلة لها جذور حقيقية مختلفة.

الآن , توصيل هذه القيم في صيغة الجذور التي نحصل عليها:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{0 \pm \sqrt{\left(0\right)^2-4\left(1\right)\left(-1\right)}}{2\cdot 1} = \displaystyle \frac{0 \pm \sqrt{4}}{2}\]

إذن , نجد ذلك:

\[ {x}_1 = \frac{0}{2}-\frac{1}{2}\sqrt{4}=\frac{0}{2}-1=-1 \] \[{x}_2 = \frac{0}{2}+\frac{1}{2}\sqrt{4}=\frac{0}{2}+1=1\]

معادلة المقام المساعد

نحن بحاجة إلى إيجاد جذور المقام: \(x+1=0\)

ولذلك, فإن حل \(x\) لمعادلة خطية معينة يؤدي إلى \(x=-1\).

البسط والمقام صفر

بناءً على التحليل الموضح أعلاه, فإن الأصفار الحقيقية لبسط الدالة النسبية المعطاة هي \( x_{ 1} = -1\) و \( x_{ 2} = 1\).

كما وجد أن المقام يحتوي على صفر حقيقي واحد, وهو \( x_{ 1} = -1\).

العثور على اعتراضات x

وبناء على أصفار البسط التي ليست أصفار المقام نجد أن هناك تقاطع x واحد وهو \(\left(1, 0\right)\).

العثور على اعتراضات y

وبتقييم الدالة المقدمة في \(x = 0\) نجد أن:

\[ f(0) = \frac{0^2-1}{0+1} = -1\]

إذن فإن تقاطع y هو \( \left(0, -1\right)\).

الخطوط المقاربة الرأسية

بعد تحليل الأصفار, نستنتج أن الدالة لا تحتوي على خطوط مقاربة رأسية.

مقاربة أفقية

لاحظ أن درجة البسط هي \(2\) ودرجة المقام هي \(1\), ومن ثم بما أن درجة كثير الحدود في البسط تزيد عن تلك الموجودة في المقام, فإننا نستنتج أنه لا يوجد أفقي الخط المقارب.

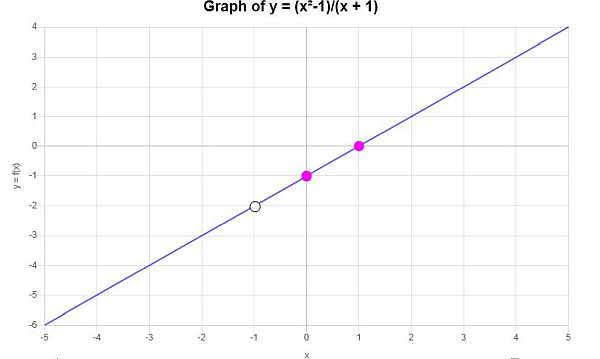
يتم الحصول على الرسم البياني التالي:

مثال: الخطوط المقاربة الأفقية

هل تحتوي هذه الدالة العقلانية على خط تقارب أفقي: \(f(x) = \frac{x^2-1}{x^2+1}\)؟

حل: من الواضح في هذه الحالة أن الدالة تتكون من حاصل قسمة كثيرتي الحدود, وكلاهما لهما درجة تساوي 2. أي أن لهما نفس الدرجة, وبالتالي يوجد خط تقارب أفقي.

يمكننا أن نرى هذا باستخدام الحدود أيضًا:

\[\lim_{x\to +\infty} f(x) = \lim_{x\to +\infty}\frac{x^2-1}{x^2+1} = \lim_{x\to +\infty}\frac{1-\frac{1}{x^2}}{1+\frac{1}{x^2}} = 1\]

مما يعني أن الخط المقارب الأفقي هو \(y = 1\). هذا يختتم الحساب.

الآلات الحاسبة وظيفة مفيدة

الوظائف هي كائنات رياضية أساسية, والتي تلخص العلاقة بين المتغيرات المختلفة. باستخدام أ حاسبة وظيفة يمكن أن تساعدك على التعامل بشكل منهجي مع الوظائف التي قد تكون معقدة للغاية بحيث لا يمكن التعامل معها يدويًا.

الرسوم البيانية وظائف عقلانية هي واحدة من أمثلة الألعاب الأكثر شيوعًا التي يتعلمها الطلاب في الجبر وحساب التفاضل والتكامل, وعلى الرغم من أن الوظائف العقلانية ربما لا تظهر في حد ذاتها في كثير من الأحيان في التطبيقات, إلا أن المهارات التحليلية المطلوبة للتعامل معها يمكن أن تكون لا تقدر بثمن

الشيء نفسه ينطبق على حل المعادلات العقلانية , حيث ستكون مبادئ معالجة التعبيرات الجبرية واختزالها إلى حدودها الأدنى قوية للغاية لتحقيق مهارات أكثر تقدمًا.

الآن, إذا كنا نتحدث عن الوظيفة, فلا يمكننا أن ننسى حساب مشتقة دالة والتكامل وغيرها من التقنيات متناهية الصغر الأكثر تقدما.