مفهوم الوظيفة مهم للغاية وهو موجود في كل مكان في الرياضيات. هذا هو السبب في أننا نحتاج إلى إعطائها فكرة جيدة , قبل محاولة فهم بعض الأشياء الجيدة التي ستأتي بعد ذلك عندما نتعمق في مواضيع التفاضل والتكامل , مثل التفاضل والتكامل.

ما هي المجموعة؟

العنصر الأول الذي نحتاج إلى فهمه هو مفهوم أ يضع . المجموعة هي ببساطة مجموعة من العناصر. إذن , يتم تعريف المجموعة ببساطة عن طريق معرفة العناصر التي تنتمي إلى المجموعة والعناصر التي لا تنتمي إلى المجموعة. يبدو أنها مهمة بسيطة للغاية ويجب اختزال نظرية المجموعة ببساطة إلى قواعد لا لبس فيها لتحديد العناصر التي تنتمي إلى المجموعة.

على سبيل المثال , دعونا نحدد مجموعة الأرقام الزوجية , ونسميها \(E\). لماذا هو حتى مجموعة؟ نظرًا لأنه يحتوي على قاعدة لا لبس فيها لتحديد العناصر التي تنتمي إلى \(E\): ينتمي الرقم الحقيقي \(x\) إلى \(E\) إذا كان قابلاً للقسمة على 2. تعمل القاعدة بشكل لا لبس فيه مع كل رقم حقيقي محدد ما إذا كان ينتمي إلى \(E\) أم لا. لماذا أقول "لا لبس فيه" وأكرر. لأنها مهمة. يعني بشكل لا لبس فيه أنه لا توجد طريقة لاستنتاج أن \(x\) ينتمي كلاهما ولا ينتمي إلى \(E\). لسوء الحظ , تتجاوز الأشياء أحيانًا خيالنا. على عكس حدسنا , يمكن أن تؤدي مجموعة قابلة للتحديد بقاعدة انتماء بسيطة إلى تصنيف انتماء غامض (متناقض) , كما يتضح من قبل برتراند راسل في مفارقته الشهيرة. أظهر راسل أنه يجب استخدام تعريف أكثر دقة لماهية المجموعة.

لجميع الأغراض العملية , سنفكر في المجموعة على أنها مجموعة من العناصر , يمكن تحديدها بقاعدة الانتماء .

ما هو منتج مجموعتين؟

لنفترض أن \(A\) و \(B\) يتم تعيينهما , في سياق التعريف الوارد أعلاه. المنتج \(A\times B\) من مجموعتين هو مجموعة أخرى , والتي يتم تعريفها على أنها مجموعة من جميع الأزواج المرتبة الممكنة من النموذج \(\left( a, b \right)\) , حيث ينتمي \(a\) إلى \(A\) و \(b\) ينتمي إلى \(B\). إذن , \(A\times B\) هي مجموعة , وعناصرها عبارة عن أزواج مرتبة من النموذج \(\left( a ,b \right)\). لا تدع هذا الترميز يثير إعجابك. عندما أقول "أزواج مرتبة من النموذج \(\left( a, b \right)\)" , فإن الرمز \(\left( a, b \right)\) هو رمز مكون , للإشارة إلى عنصر يتكون من كيانين \(a\) و \(b\) , وتحديد العنصر الأول على أنه \(a\) , والعنصر الثاني على أنه \(b\) . هذا كل شيء. بدلاً من \(\left( a,b \right)\) , كان بإمكاننا اختيار الرمز \(a\_b\) , وكان سيعمل بشكل جيد.

يجب أن تسامحني , لكن يجب أن أكتب التعريف الرياضي لحاصل ضرب مجموعتين (يمكننا أيضًا مضاعفة المجموعات ... ما رأيك , سنتوقف بالأرقام فقط , أه؟):

\(A\times B=\left\{ \left( a,b \right):\,\,\,a\in A,\,\,\,b\in B \right\}\)

السبب في أنني أكتب التعريف هو أن تنظر إليه وتتعرف على كيفية استخدام تدوين مضغوط للغاية نقوله تمامًا بنفس الطريقة التي حددتها بها بالكلمات الواردة في الفقرة أعلاه. آمل أن تخفف بعض الخوف من قراءة عبارات الرياضيات. قد يكون علماء الرياضيات أشخاصًا غير تقليديين في بعض الأحيان , لكنهم يجدون رموزًا جيدة وواضحة ومضغوطة. وبالتالي , فإن لغة الرياضيات سهلة القراءة. حق؟ حق؟ من فضلك قل لي أنني على حق ...

ملاحظة جانبية , لأسباب تاريخية , يُشار عادةً إلى منتج مجموعتين \(A\times B\) باسم أ المنتج الديكارتي .

الآن , تعريف الوظيفة (نهائيًا)

حسنًا , لقد كذبت , هناك خطوة أخرى قبل تحديد الوظيفة. نحن بحاجة إلى تحديد مفهوم علاقة . ما هي العلاقة؟ إلى جانب استخدامها الشائع ككلمة إنجليزية , فإن العلاقة هي ببساطة مجموعة فرعية من المنتج الديكارتي. أي مجموعة فرعية من المنتج الديكارتي هي علاقة. إذن , إذا كانت \(A\) و \(B\) عبارة عن مجموعات , فإن المجموعة \(R\) هي علاقة إذا \(R\subseteq A\times B\). نظرًا لأن أي مجموعة يمكن اعتبارها مجموعة فرعية من نفسها , فإن جميع المنتجات الديكارتية هي علاقات بحد ذاتها.

ضعه على إطار:

العلاقة هي مجموعة هي مجموعة فرعية من منتج ديكارتي

دعونا نحصل على المزيد من الرسوم البيانية. ضع في اعتبارك المجموعة \(A=\left[ 0,1 \right]\) (وهي جميع الأعداد الحقيقية الأكبر من أو تساوي 0 , وهي أيضًا أقل من أو تساوي 1). ما هو المنتج الديكارتي \(A\times A\)؟ دعونا نببغاء ما تعلمناه للتو. المنتج الديكارتي \(A\times A\) هو \(\left[ 0,1 \right]\times \left[ 0,1 \right]\) في هذه الحالة هو مجموعة كل الأزواج\(\left( x, y \right)\) , حيث ينتمي كل من \(x\) و \(y\) إلى \(\left[ 0,1 \right]\). عادة ما تكون المنتجات الديكارتية سهلة الرسم البياني. انظر إلى المنطقة المظللة أدناه:

الآن , ما الذي يجعل العلاقة؟ يمكننا "اقتطاع" كل ما نريد المنطقة المظللة أعلاه , وما يتبقى هو علاقة في \(\left[ 0,1 \right]\times \left[ 0,1 \right]\). على سبيل المثال , يمكننا قطع "الزوايا" للحصول على المنطقة الفرعية التالية:

المنطقة (المحددة) أعلاه هي علاقة. لماذا ا؟ لأنها مجموعة فرعية من المنتج الديكارتي \(\left[ 0,1 \right]\times \left[ 0,1 \right]\). لكن يمكننا اقتطاع المزيد. ماذا عن اقتطاع ربع دائرة؟ انظر المنطقة أدناه.

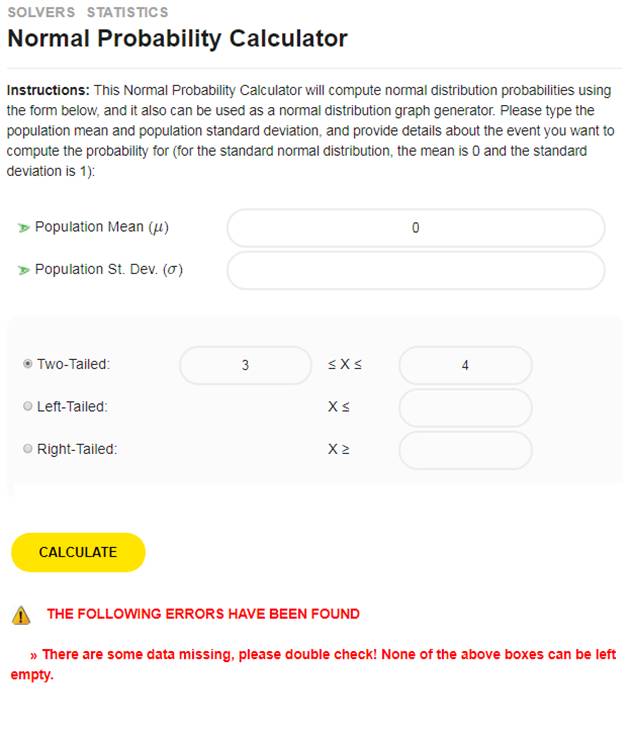
المنطقة (المحددة) أعلاه هي علاقة. لماذا ا؟ مرة أخرى , لأنها مجموعة فرعية من المنتج الديكارتي \(\left[ 0,1 \right]\times \left[ 0,1 \right]\).

الآن , اسمحوا لي أن أقدم لكم مثالاً على علاقتين في \(\left[ -1,1 \right]\times \left[ -1,1 \right]\). انظر الرسوم البيانية أدناه:

العلاقة 1

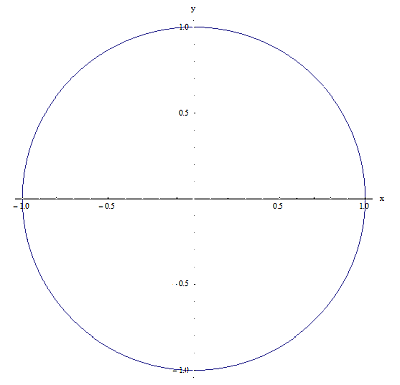
العلاقة 2

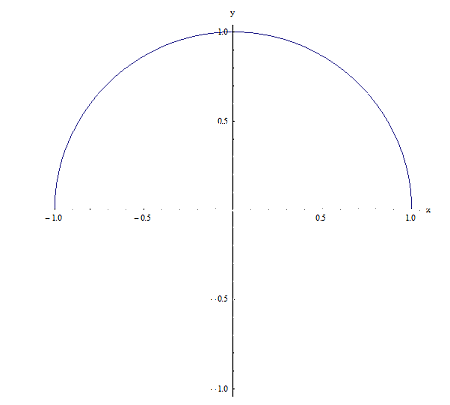
من الواضح أن كلاهما علاقات (لأن كلاهما وارد في المنتج الديكارتي \(\left[ -1,1 \right]\times \left[ -1,1 \right]\) , لكن بينهما اختلاف رئيسي واحد: بالنسبة للعلاقة 1 , بالنسبة لنقطة معينة x في \(\left[ -1,1 \right]\) , هناك نقطتان \({{y}_{1}}\) و \({{y}_{2}}\) لهما الخاصية التي \(\left( x,{{y}_{1}} \right)\) و \(\left( x,{{y}_{2}} \right)\) بالنسبة للعلاقة 1. على سبيل المثال بالنسبة إلى x = 0 , هناك نقطتان \({{y}_{1}}=1\) و \({{y}_{2}}=-1\) مثل أن \(\left( 0,1 \right)\) و\(\left( 0,-1 \right)\) تنتمي إلى العلاقة 1. الآن , بالنسبة للعلاقة 2 ليس هذا هو الحال لأنه , على سبيل المثال , بالنسبة إلى x = 0 , يكون \(y=1\) فقط يجعل النقطة \(\left( 0,1 \right)\) تنتمي إلى العلاقة 1.

أخيرًا يمكننا تحديد وظيفة: الوظيفة \(R\) هي مجموعة ذات علاقة ولها أيضًا خاصية أنه إذا كانت النقطة \(\left( x,y \right)\) تنتمي إلى \(R\) , فلا توجد نقطة أخرى \(\bar{y}\) مختلفة عن \(y\) لها الخاصية التي تنتمي إلى __XYZ_EZ_A___ أيضا. بمعنى آخر , الوظيفة هي علاقة مع المتطلبات الإضافية التي تقترن كل \(x\) في مجالها مع \(y\) واحد فقط.

كيف تعرف كيف تفرق بين دالة وعلاقة ؟؟

الأدوات! نستخدم خدعة صغيرة تسمى "اختبار الخط العمودي": نرسم خطًا رأسيًا وهميًا , ونقوم بتحريكه من اليسار إلى اليمين على طول الطريق , ونرسم خريطة ذهنية لمكان تقاطع الخط العمودي مع العلاقة.

• إذا تقاطع الخط العمودي في أي نقطة مع العلاقة عند أكثر من نقطة واحدة , فإن العلاقة تفشل في اختبار الخط العمودي , ومن ثم لا تكون العلاقة دالة

• إذا كان الخط العمودي في أي نقطة لا يتقاطع مع العلاقة في أي مكان عند أكثر من نقطة واحدة , فإن العلاقة تمر باختبار الخط العمودي , ومن ثم تكون العلاقة دالة

انظر إلى المثالين أدناه:

مثال 1: فشل في اختبار الخط العمودي لأن الخط العمودي الموضح في الشكل يتقاطع مع العلاقة في أكثر من نقطة واحدة: ليست وظيفة

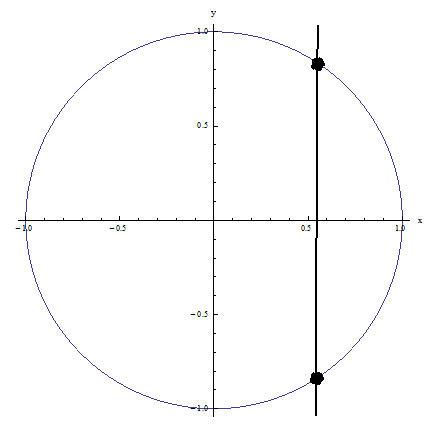
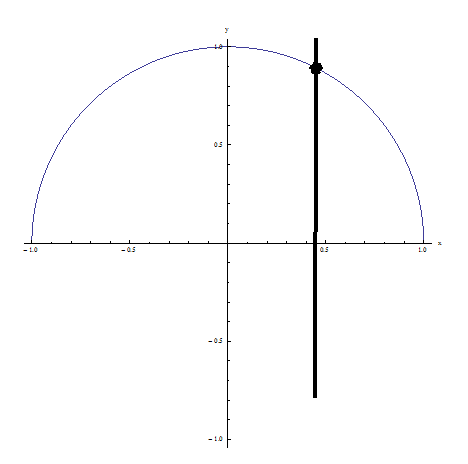
مثال 2: اجتاز اختبار الخط العمودي لأنه لا يوجد خط عمودي يتقاطع مع العلاقة عند أكثر من نقطة واحدة: إنها وظيفة!

هناك العديد من التطبيقات الرسومية التي يمكن إجراؤها بوظائف , بما في ذلك حساب الخطوط المقاربة الأفقية والخطوط المقاربة العمودية والخطوط المقاربة المائلة إن أمكن.