حاسبة الحجم الطويل متعدد الحدود

تساعدك هذه الآلة الحاسبة معك في عملية إجراء تقسيم طويل بين اثنين من الحدود المعطى.تحقيقًا لهذه الغاية , تحتاج إلى تقديم تعبيرين متعدد الحدود صالحين.ربما تكون هذه الحدود مبسطة بالفعل أم لا , وستبسيط الحاسبة لها إذا احتجت إليها.

متي Tقacym mtudad alحdod تحتاج إلى توفير اثنين من الحدود , واحدة التي ستقسمها , والتي تسمى الأرباح , والآخر هو المقسوم.

بمجرد تقديم اثنين ساري المفعول كثyer الدادود , تتمثل الخطوة التالية في النقر على زر "حساب" , والذي سيظهر جميع الحساب المقابل المطلوب للتقسيم الطويل المطلوب بين كثير الحدود المقدمة.

عملية إجراء تقسيم متعدد الحدود باستخدام طrive altقym alطoyalة هي طريقة واضحة نسبيًا , ولكنها تتطلب مقاربة منظمة للغاية , حتى لا تضيع.عادة , يعمل بشكل أفضل باستخدام نهج جدولي لإظهار الخطوات المقابلة.

يتم استخدام نهج أبسط مع توم الله , لكن هذا ينطبق فقط عندما يكون المقسوم لديه درجة واحدة , لذلك يكون له وصول محدود أكثر

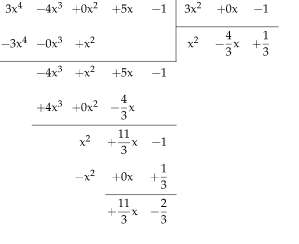
ما هو كثير الحدود؟

كثير الحدود هو نوع من التعبير البسيط الذي يجمع بين المبالغ وطرح صلاحيات عدد صحيح من متغير معين x (أو أي اسم متغير يتم اختياره) , وربما مضروبة في الثوابت.

على سبيل المثال , التعبير \(p(x) = 2x^2 + x + 1\) هو مزيج من المصطلحات \(2x^2\) , \(x\)\(x^0 = 1\).

من ناحية أخرى , \(f(x) = 2x^2 + \sin(x) + 1\) ليس متعدد الحدود , لأن المصطلح \(\sin(x)\) ليس قوة x.

العمليات متعددة الحدود

كثير الحدود , مثل الأرقام , يمكن تشغيلها مع alإضaفة , alطrح .الإضافات والطرح بسيطة للقيام بها , بطريقة بديهية للغاية.على سبيل المثال , إذا كان لديك اثنين من الحدود , \(p(x) = 2x+1\) و \(q(x) = x^3 + 2x+ 3\) , يتم تحقيق إضافة متعدد الحدود عن طريق إضافة المصطلحات حرفيا مثل

\[p(x) + q(x) = 2x + 1 + x^3 + 2x+ 3 = x^3 + 4x + 4\]

بالنسبة للطرح , يمكنك أيضًا طرح الشروط المقابلة من متعدد الحدود التي يتم طرحها.على سبيل المثال , إذا كان لديك نوعين من الحدود , \(p(x) = 2x+1\) و \(q(x) = x^3 + 2x+ 3\) , فعندئذ يتم طرحه مثل

\[p(x) - q(x) = 2x + 1 - (x^3 + 2x+ 3) = 2x + 1 - x^3 - 2x - 3) = -x^3 -2\]

الضرب أكثر تعقيدًا , لأنه يتعين عليك شروطًا متعددة الاستخدامات باستخدام خاصية التوزيع:

\[p(x) \cdot q(x) = (2x + 1) \cdot (x^3 + 2x+ 3) = 2x \cdot x^3 + 2x \cdot 2x + 2x \cdot 3 + 1\cdot x^3 + 1\cdot1 2x+ 1\cdot 3 = 2x^4 +x^3+4x^2+8x+3\]

الانقسام أكثر تعقيدًا قليلاً , لأنه ينطوي على فكرة أن متعدد الحدود قد لا يقسم بالضبط متعدد الحدود.من الناحية الرياضية , عندما يكون لدينا متعدد الحدود \(p(x)\) و \(s(x)\) , ونريد أن نقسم \(p(x)\) بواسطة \(s(x)\) , نحن نبحث عن حاصل << xyzc> وبعد الباقي\(r(x)\) (كلاهما كثير الحدود) , التي لها خاصية \(p(x)= q(x)\cdot s(x) + r(x)\) , مع الحالة التي درا معدد الدة \(r(x)\) أقل من درجة \(s(x)\).هذا عادة ما يسمى تالللي وبعد

طريقة التقسيم الطويل

لذا , فإن طريقة التقسيم الطويلة هي إحدى الطرق المنهجية للبدء مع اثنين من الحدود التي نريد تقسيمها \(p(x)\)طريقة ذلك

\[p(x)= q(x)\cdot s(x) + r(x)\]

هذه الخوارزمية مفيدة للغاية , وعلى الرغم من أن المشكلة تبدو بسيطة في المظهر , فليس من الصعب أن تضيع إذا لم تكن تستخدم نهجًا منهجيًا , حيث يضمن الوصول إلى الحاصل والباقي المطلوب.

ما هي خطوات القيام بتقسيم طويل؟

• الظهر 1: حدد اثنين من الحدود p (x) و s (x) التي تريد تقسيمها وتحديد p (x) على أنها توزيعات الأرباح و s (x) كقسامة
• ال alخطoة 2: تحقق من درجة الأرباح P (X) مقابل درجة S (X).إذا كانت درجة S (x) أكبر من درجة p (x) , فلدينا أن الباقي هو توزيع الأرباح p (x) نفسه , و quient هو صفر: q (x) = 0 , وأنك قد انتهيت
• الله 3: في هذه الحالة , نفترض أن درجة الأرباح P (X) أكبر من أو تساوي درجة القسم S (X) , وإلا , فقد توقفنا في الخطوة 2
• الظهر 4: نحتاج إلى إجراء عملية تكرارية لإيجاد ما تبقى مؤقتًا , حتى وصلنا إلى الباقي على درجة أقل من درجة S (X)
• الظهر 5: يتم تحديث الباقي المؤقت أو المؤقت في كل مرة عن طريق العثور أولاً على النسبة بين أعلى مدة من الباقي المؤقت الحالي والمقاطع S (X).تتضاعف هذه النسبة (وهو مصطلح الطاقة) ثم S (x) , ويتم طرح نتيجة هذا الضرب من الباقي المؤقت الحالي , مما يؤدي إلى باقي محدث
• ال 6: تستمر هذه العملية حتى تحصل الباقي على درجة أقل من درجة S (X).في كل خطوة من التكرار , يتم تقليل درجة الباقي المؤقت بمقدار 1 على الأقل , وبالتالي فإن العملية مضمونة لإنهاء

في النهاية , عملية Tقacym alثnyn kn alحdod يتم تقليلها إلى حساب مضاعفات هي مبالغ متعددة الحدود , وهو ما يحدث إلى حد كبير مع الأرقام.طريقة التقسيم الطويل للعديد من الحدود هي تمديد الطريقة التي نقسم بها الأرقام إلى كثير الحدود.

كيف يرتبط الانقسام الطويل بإيجاد جذور معادلة متعددة الحدود

افترض أن p (x) هو الأرباح التي تريد تقسيمها , و s (x) هي المقسوم.وفقًا لطريقة التقسيم الطويل , ستتمكن من العثور على Q (x) و R (x) الباقي بحيث:

\[\displaystyle p(x) = q(x)s(x) + r(x) \]

ولكن في بعض الأحيان , يحدث أن الباقي هو r (x) = 0 , وفي هذه الحالة نقول أن s (x) يقسم p (x) (أو يقسم p (x) بالضبط).لذلك , عندما r (x) = 0

\[\displaystyle p(x) = q(x)s(x) \]

يشير هذا إلى أنه من أجل العثور على جذور p (x) = 0 , يمكننا الحصول على حل Q (x) = 0 و s (x) = 0 , بشكل منفصل , وهي معادلات أبسط لحلها.

مزايا هذه الآلة الحاسبة الطويلة

كما ذكرت من قبل , فإن الانقسام الطويل ليس صعبًا للغاية , لكنه يتطلب نهجًا منهجيًا.ميزة كبيرة لاستخدام أ حASBة توم مثل هذا هو أنك ستحصل على جميع خطوات العملية المعروضة

قد لا يكون من الضروري معرفة كيفية إجراء الخطوات بنفسك , لكن هذه الآلة الحاسبة تتيح لك معرفة كيفية القيام بذلك , مع كل خطوة شرح , إزالة لغز الحصول على الباقي والحصص , على سبيل المثال حاسبة رقمية , والتي ستقدمأنت الجواب دون إظهار الخطوات.

تضمن حاسبة تقسيم طويلة مع خطوات توضح جميع العمل أن تحصل على فكرة واضحة عما يحدث مع الحساب.

مثال: حساب تقسيم متعدد الحدود

حساب تقسيم متعدد الحدود التالي: \(p(x) = \frac{1}{3} x^3 + \frac{5}{4}x - \frac{5}{6}\) و \(s(x) = x+3\).

الملم: تم توفير متعدد الحدود التالية: \(\displaystyle p(x) = \frac{1}{3}x^3+\frac{5}{4}x-\frac{5}{6}\) , والتي يجب أن تقسمها الحدود \(\displaystyle s(x) = x+3\).

لاحظ أن درجة الأرباح هي \(\displaystyle deg(p) = 3\) , في حين أن درجة المقسوم هي \(\displaystyle deg(s)) = 1\).

الظهر 1: المصطلح الرائد للموزى \(\displaystyle p(x) = \frac{1}{3}x^3+\frac{5}{4}x-\frac{5}{6}\) هو \(\displaystyle \frac{1}{3}x^3\) , في حين أن المصطلح الرئيسي للمقاطع \(\displaystyle s(x) = x+3\) يساوي \(\displaystyle x\).

إذن , فإن المصطلح الذي نحتاجه إلى مضاعفة \(x\) للوصول إلى المصطلح الرائد من الأرباح هو \(\displaystyle \frac{ \frac{1}{3}x^3}{ x} = \frac{1}{3}x^2\) , لذلك نضيف هذا المصطلح إلى الحاصل.أيضًا , نحن نضاعف هذا من خلال المقسوم للحصول على \(\displaystyle \frac{1}{3}x^2 \cdot \left(x+3\right) = \frac{1}{3}x^3+x^2\) , والذي نحتاج إلى طرحه على توزيعات الأرباح:

\[\begin{array}{rcccc} &\displaystyle \frac{1}{3}x^2 & \displaystyle & \displaystyle &\\[0.8em] \hline x+3\,) & \displaystyle \frac{1}{3}x^3 & \displaystyle & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle -\frac{1}{3}x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \end{array}\]

ال alخطoة 2: في هذه الحالة , فإن المصطلح الرئيسي للباقي الحالي \(\displaystyle -x^2+\frac{5}{4}x-\frac{5}{6}\) هو \(\displaystyle -1x^2\) , ونحن نعرف أن المصطلح الرئيسي للمقاطع هو \(\displaystyle x\).

إذن , فإن المصطلح الذي نحتاجه إلى مضاعفة \(x\) للوصول إلى المصطلح الرئيسي للباقي الحالي هو \(\displaystyle \frac{ -1x^2}{ x} = -x\) , لذلك نضيف هذا المصطلح إلى الحاصل.أيضًا , نضاعف هذا من خلال المقسوم للحصول على \(\displaystyle -x \cdot \left(x+3\right) = -x^2-3x\) , والذي نحتاج إلى طرحه للتذكير الحالي:

\[\begin{array}{rcccc} &\displaystyle \frac{1}{3}x^2 & \displaystyle -x & \displaystyle &\\[0.8em] \hline x+3\,) & \displaystyle \frac{1}{3}x^3 & \displaystyle & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle -\frac{1}{3}x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle +3x & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle \frac{17}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \end{array}\]

الله 3: في هذه الحالة , فإن المصطلح الرئيسي للباقي الحالي \(\displaystyle \frac{17}{4}x-\frac{5}{6}\) هو \(\displaystyle \frac{17}{4}x\) , ونحن نعرف أن المصطلح الرئيسي للمقاطع هو \(\displaystyle x\).

إذن , فإن المصطلح الذي نحتاجه إلى مضاعفة \(x\) للوصول إلى المصطلح الرئيسي للباقي الحالي هو \(\displaystyle \frac{ \frac{17}{4}x}{ x} = \frac{17}{4}\) , لذلك نضيف هذا المصطلح إلى الحاصل.أيضًا , نضاعف هذا من خلال المقسوم للحصول على \(\displaystyle \frac{17}{4} \cdot \left(x+3\right) = \frac{17}{4}x+\frac{51}{4}\) , والذي نحتاج إلى طرحه للتذكير الحالي:

\[\begin{array}{rcccc} &\displaystyle \frac{1}{3}x^2 & \displaystyle -x & \displaystyle +\frac{17}{4}&\\[0.8em] \hline x+3\,) & \displaystyle \frac{1}{3}x^3 & \displaystyle & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle -\frac{1}{3}x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle +3x & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle \frac{17}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle & \displaystyle & \displaystyle -\frac{17}{4}x & \displaystyle -\frac{51}{4}\\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle & \displaystyle -\frac{163}{12}\\[0.8em] \end{array}\]

الذي يخلص إلى هذا الحساب , لأن درجة الباقي الحالي \(r(x) = -\frac{163}{12}\) أقل من درجة المقسوم \(s(x) = x+3\).

استنتاج: Therefore, we conclude that for the given dividend \(\displaystyle p(x) = \frac{1}{3}x^3+\frac{5}{4}x-\frac{5}{6}\) and divisor \(\displaystyle s(x) = x+3\), we get that the quotient is \(\displaystyle q(x) = \frac{1}{3}x^2-x+\frac{17}{4}\) and the remainder is \(\displaystyle r(x) = -\frac{163}{12}\), and that