حاسبة مشتقة
عاليمت: استخدم هذه الآلة الحاسبة المشتقة لإيجاد مشتق من الوظيفة التي تقدمها , مما يوضح جميع خطوات العملية.يرجى كتابة الوظيفة التي تريد حساب المشتق في المربع أدناه.
حاسبة مشتقة
ستأخذك هذه الآلة الحاسبة المشتقة عبر جميع الخطوات والقواعد المستخدمة للعثور على مشتق وظيفة معينة.يجب أن تكتب في وظيفة مثل 3x + sin (x^2) , أو يمكنك فعليًا مقدمةها مع تعريف الوظيفة بأكملها , مثل f (x) = 3x^2 + 2tan (x^3).
لاحظ أنه يمكن الإشارة إلى ذلك على أنه حاسبة مشتقة أولى مثل حاسبة مشتقة.يمثل المشتق والمشتق الأول نفس الشيء , وعادة ما يتم إسقاط الجزء "الأول".
قد تأتي الوظيفة المقدمة مبسطة تمامًا أو لا , لا يهم , لأن الآلة الحاسبة ستقوم أولاً بتبسيط الوظيفة إذا لزم الأمر قبل حساب مشتقها.
مرة وويه تم توفيره , تحتاج فقط إلى النقر على "حساب" , وانتظر بضع ثوان , وسيتم تقديم جميع خطوات الحساب إليك.
التمايز هو الأداة الرئيسية المستخدمة في حساب التفاضل والتكامل (جنبا إلى جنب مع التكامل) وهي عملية حاسمة تستخدم على نطاق واسع في الرياضيات الأكثر تقدما.تتضمن بعض التطبيقات الشائعة جدًا ح ساب خط إل و Maxima و Minima وأكثر من ذلك بكثير.
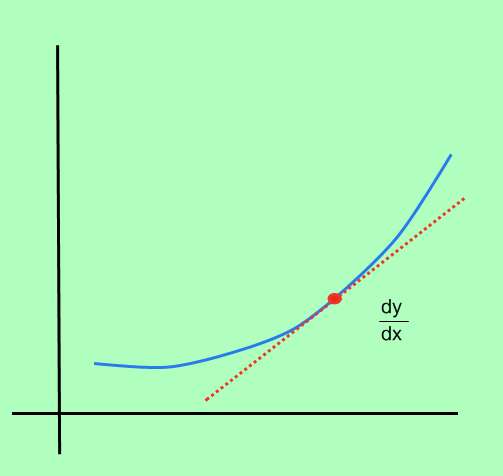
كيفية حساب مشتق الوظيفة؟
يتم استدعاء عملية حساب مشتق الوظيفة آلتاكل , ويتألف من تحديد معدل تغيير النقطة الفورية , في كل نقطة في مجال الوظيفة.
ما هو معدل تغيير الوظيفة الفوري؟حسنًا , لنبدأ بتعريف مدال آلتوير : النظر في وظيفة \(f\), وافترض أن لدينا نقطتان , \(x_0\)و \(x_1\).في النقطة \(x_0\), الوظيفة هي \(f(x_0)\), وفي النقطة \(x_1\), تأخذ الوظيفة القيمة \(f(x_1)\)
بعد ذلك , يتم تعريف التغيير في F على أنه \(\Delta y = f(x_1) - f(x_0)\) (والذي يشار إليه أيضًا باسم التغيير في Y).أيضا , يتم تعريف التغيير في x على أنه \(\Delta x = x_1 - x_0)\).بالكلمات البسيطة , \(\Delta x\) هو التغيير في x , في حين أن \(\Delta y\) هو التغيير في قيمة الوظيفة , بسبب التغيير في x.
بيانياً:
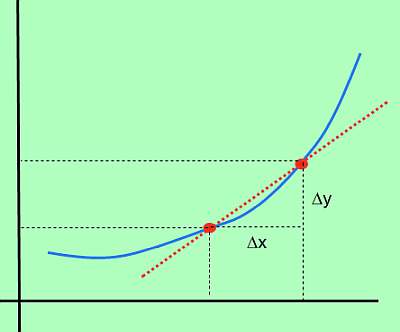
صيغة مشتقة
لذلك , إذا كان\(\Delta x\) يمثل التغيير في x , ويمثل\(\Delta y\) التغيير في قيمة الوظيفة , بسبب التغيير في x , المقابل مدال آلتوير يكون:
\[\text{Rate of Change} = \displaystyle \frac{\Delta y}{\Delta x} \]إذن , ماذا سيكون معدل التغيير الفوري؟هذا من شأنه أن يتوافق مع تحليل ما سيحدث إذا أصبح \(\Delta x\) صغيرًا حقًا.يتوقع المرء أن يصبح \(\Delta y\)صغيرًا أيضًا , لكن ذلك سيحدث للمعدل بين \(\Delta y\)و \(\Delta x\)؟
لذلك , في هذا السياق , يتم تعريف معدل التغيير الفوري على أنه
\[\text{Instant Rate of Change} = \displaystyle \lim_{x_1 \to x_0}\frac{\Delta y}{\Delta x} \]لذلك , بعبارات Layman , قمنا بتعيين \(x_0\)ثابت ونحسب معدل التغيير لقيم \(x_1\)التي تكون أقرب وأقرب إلى \(x_0\).باستخدام فكرة التغيير الفوري هذه , يمكننا إعطاء الصيغة التالية للمشتق عند نقطة \(x_0\).
\[f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{\Delta y}{\Delta x} = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \]في حالة خروج الحد المذكور أعلاه , نقول أن الوظيفة F قابلة للتمييز في \(x_0\).أيضًا , سوف نقول أن الوظيفة قابلة للتمييز في مجموعة A , إذا كانت الوظيفة قابلة للتمييز في كل نقطة من المجموعة.
خطوات لاستخدام الصيغة المشتق
- الظهر 1: حدد بوضوح الوظيفة F التي تريد التمييز
- ال alخطoة 2: تأكد من تبسيط F قدر الإمكان , وإلا فإن العثور على الحد المطلوب قد يكون أصعب بشكل غير ضروري
- الله 3: قرر ما إذا كنت ستعمل مع نقطة عامة X0 , أو أنك تعطي نقطة رقمية محددة لـ X0
- الظهر 4: بناءً على تعريف الوظيفة , استخدم الصيغة \(f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \).هذا , قم بتوصيل قيم X0 و X1 في F , وشاهد كيف تبدو الصيغة جبريًا
- الظهر 5: تبسيط قدر الإمكان قبل أخذ الحد
- ال 6: في بعض الأحيان يكون من الأسهل ضبط x1 = x0 + h , ثم حساب الحد كما يتقارب H إلى 0
لاحظ أن الخطوة 6 هي واحدة يحبها بعض الأشخاص.في الواقع , فإن الصيغة المشتقة البديلة التي قد تبدو أسهل لأغراض التبسيط هي:
\[f'(x_0) = \displaystyle \lim_{h \to 0} \frac{f(x_0 + h) - f(x_0)}{h} \]وهي الصيغة التي قد تجدها في كتابك المدرسي , بدلاً من الآخر.
قواعد مشتقة
يبدو الأمر وكأنه الكثير من العمل لحساب المشتق باستخدام الصيغة.وبالفعل , قد تكون عملية شاقة إذا قررنا تحديد كل عملية تمايز باستخدام صيغة المشتق.
لحسن الحظ , هناك عدد من الوظائف (أي كثyer الدادود و الداول الملمس ) التي نعرفها بدقة ما هو مشتقهم.
علاوة على ذلك , لدينا قoaud altmaiز التي تسمح لنا بالعثور على مشتق وظيفة هي أ الويسى و/أو مجموعة من الوظائف الأولية (التي نعرف مشتقاتها) , من حيث المشتقات الأولية.
ما هي الخطوات لحساب المشتق؟
- الظهر 1: تحديد الوظيفة F التي تريد التمييز.تبسيط قدر الإمكان قبل حساب مشتقه
- ال alخطoة 2: حدد ما إذا كنت مطلوبًا من استخدام الصيغة المشتقة أم لا
- الله 3: إذا كان يجب عليك استخدام الصيغة المشتقة , فاستخدم \(f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \), أو يمكنك استخدام \(f'(x_0) = \displaystyle \lim_{h \to 0}\frac{f(x_0+h) - f(x_0)}{h} \)إذا كان من الأسهل الاقتراب
- الظهر 4: إذا لم تكن مطلوبًا من استخدام الصيغة المشتقة , فيمكنك استخدام قواعد التمايز الرئيسية: الخطية , سيدا و قaudة alحaصl و قaudة السلم , والتي ستساعدك على تقليل حساب المشتق لاستخدام المشتقات المعروفة الأساسية
في كثير من الأحيان , الوظيفة التي تحاول الهاور على الله لأنها ليست وظيفة بسيطة , لكنها مزيج أساسي من العديد من الوظائف البسيطة.على سبيل المثال , الوظيفة
\[f(x) = x + \cos(x) + \sin(x)\]ليست وظيفة أولية في حد ذاتها , لكنها كذلك الويسى من ثلاث وظائف أولية , \(x\), \(\sin x\)و \(\cos x\).
تطبيقات المشتقات
يمكن للمرء أن يفكر "حسنًا , المشتقات تنطوي على حدود وهذا نظري للغاية , لذلك يجب ألا يكون لديه الكثير من التطبيقات" , لكنك ستكون مخطئًا تمامًا.سحر المشتقات هو أنها تتعلق بشكل أساسي بمعدل تغيير الوظائف , والتي يمكن أن تمثل أنواعًا مختلفة من العمليات.
هذا هو السبب في أن التمايز يسمح بدراسة عملية التغيير , وكيفية مقارنة المتغيرات المتغيرة , والتي لها قابلية للتطبيق الواسعة.
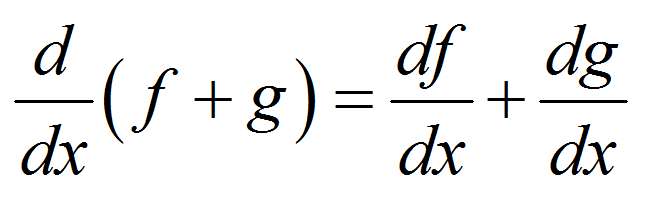
مثال: حساب المشتق
احسب المشتق فيما يتعلق بـ x لـ \(f(x) = \displaystyle \frac{x}{3} + \frac{5}{4} \cos(x) - \frac{5}{4} \sin(x^2)\)
إل: تم توفير الوظيفة التالية: \(\displaystyle f(x)=\frac{x}{3}+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right)\), والتي نحتاج إلى حساب مشتقها.
خطoة أolelyة: في هذه الحالة , نحتاج أولاً إلى تبسيط الوظيفة المحددة \(\displaystyle f(x)=\frac{x}{3}+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right) \), ومن أجل القيام بذلك , نقوم بإجراء خطوات التبسيط التالية:
بعد تبسيط الوظيفة , يمكننا المتابعة إلى حساب المشتق:
يتم الحصول على المؤامرة التالية لـ \(\displaystyle f(x)=\frac{1}{3}x+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right)\)على الفاصل الزمني \([-5, 5]\):
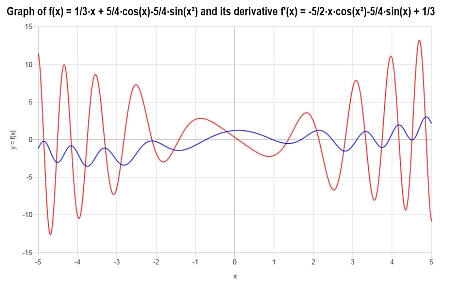
مثال: التمييز بين وظيفة
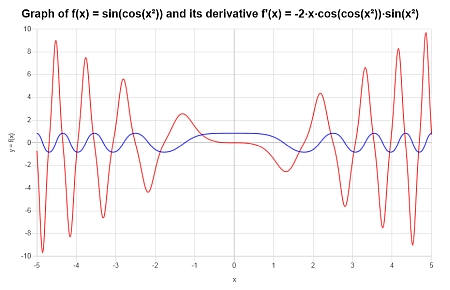
احسب مشتق: \(f(x) = \sin(\cos(x^2))\), وقدم الرسم البياني لـ \(f(x)\)و \(f'(x)\).
إل: الآن لدينا \(\displaystyle f(x)=\sin\left(\cos\left(x^2\right)\right)\).
The function came already simplified, so we can proceed directly to compute its derivative. By using this derivative cal we get:
لذلك , نحصل على المؤامرة التالية للوظيفة في الفاصل الزمني \([-5, 5]\):
مثال: حاسبة مشتقة
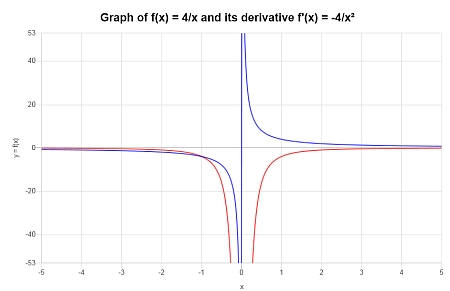
العثور على مشتق \( f(x) = \displaystyle \frac{4}{x}\).هل هو محدد بشكل جيد في كل مكان؟رسم بياني.
إل: الوظيفة المقدمة التي يلزم المشتق هي \(\displaystyle f(x)=\frac{4}{x}\).
لا يوجد حاجة إلى مزيد من التبسيط , حتى نتمكن من المضي قدمًا مباشرة لحساب مشتقاته:
بيانياً:
المزيد عن المشتقات والوظائف
هذا آlة حaSbة mشtقة be سوف يثبت لك مفيدًا جدًا لأنه سيجري حساب مشتق أي وظيفة معينة , مما يوضح جميع خطوات العملية , وتطبيق ما هو مناسب قoaudd amشtقة , وإخبارك عندما يتم تطبيقها ولماذا.
يمكن أيضًا استدعاء هذه الآلة الحاسبة حaSbة dy dx أو حASBة alحaصl altفaضly بما أن هذا هو بالضبط ما يفعله , فإنه يحسب الحد من نسبة DY/DX مع اقتراب DX إلى 0.
الوظائف هي بنيات مهمة للغاية في الرياضيات.جنبا إلى جنب مع التمايز , تحتاج إلى أن تكون قادرا تيبسي و عادة , باعتبارها ديباجة الحسابات الأخرى المتخصصة.هناك أنواع خاصة من الوظائف التي تسمح لك بإجراء عمليات محددة , مثل ما تفعله الصخور معدود .
ومن المثير للاهتمام , الكثير من العناصر المهمة مثل العثور على إحداثيات قmة المفاصل يمكن اشتقاقها بطريقة ذكية باستخدام الحجج الهندسية , يمكن الحصول عليها بشكل تافه باستخدام التمايز.
أيضا , فكرة خط alظl و طريف مان الهاول يظهر بشكل طبيعي , ينبع من مفهوم المشتق , والتمديد الطبيعي.



