المزيد عن مخطط الاحتمالات الطبيعية

مخطط الاحتمال الطبيعي هو مخطط يستخدم عادة لتقييم طبيعية التوزيع الذي تنتمي إليه بيانات العينة المرسلة.

هناك أنواع مختلفة من مخططات التوزيع الطبيعي (PP, QQ, وغيرها), ولكنها جميعًا تعمل على نفس الفكرة. تُرسم النسب المئوية النظرية للتوزيع الطبيعي القياسي بيانيًا مقابل النسب المئوية المرصودة.

لذلك, إذا كانت بيانات العينة تأتي من السكان الموزعون بشكل طبيعي , ثم يجب أن يبدو مخطط الاحتمال الطبيعي مثل 45 ^س خطٌّ مع اختلافاتٍ عشوائيةٍ حوله. إذا لم يكن الأمر كذلك, وكان نمطُ مُخطَّط الاحتمال الطبيعيّ يختلفُ بشكلٍ كبيرٍ/منهجيّ عن مُخطَّط الاحتمال الطبيعيّ, فينبغي الشكُّ في أنَّ التوزيعَ غيرُ طبيعيّ.

كيف تحسب مخطط الاحتمال الطبيعي؟

هناك عدة خطوات ملموسة يجب عليك اتخاذها, بترتيب محدد لبناء رسم احتمالي طبيعي

1. في هذه الحالة الملموسة, يتم ترتيب البيانات بترتيب تصاعدي, ونطلق على هذه البيانات اسم \(X_1, X_2, ...., X_i , ...., X_n\).
2. بالنسبة لكل \(X_i\) في هذا التسلسل من البيانات المرتبة, نقوم بحساب الترددات النظرية \(f_i\), والتي يتم تقريبها باستخدام الصيغة التالية:
\[ f_i = \frac{i - 0.375}{n + 0.25} \] (where \(i\) corresponds to the position in the ordered dataset)
3. ثم نقوم أيضًا بحساب \(z_i\), وهو ما يتوافق مع الدرجة Z المرتبطة به
\[ z_i = \Phi^{-1}(f_i)\]
4. بعد ذلك, يتم الحصول على مخطط الاحتمال الطبيعي عن طريق رسم قيم X المرتبة (بيانات العينة الخاصة بك) على المحور الأفقي, وقيم \(z_i\) المقابلة على المحور الرأسي.

مخطط الاحتمالات الطبيعية في excel

يمكنك رسم مخطط احتمالي عادي في برنامج Excel, لكن الأمر يستغرق بعض الوقت

آلات حاسبة للتوزيع الطبيعي وغيره

من بين صناع المخططات الآخرين الذين يمكنك استخدامهم: مُرسِم التوزيع الطبيعي , صانع مؤامرة مبعثر أو لدينا صانع باريتو الرسم البياني .

مثال: حساب مخطط الاحتمال الطبيعي

سؤال :يتم تزويدك بالبيانات النموذجية التالية: 2, 3, 4, 3, 3, 2, 3, 4, 5, 3, 2, 3, 1, 2, 3, 4, 5, 6, 3, 2, 4, 5, 6 10 10 10 12 12 1 2 3 3 و23. قم بإنشاء رسم بياني للاحتمالية الطبيعية.

حل:

نحتاج إلى إنشاء مخطط احتمالي طبيعي. هذه هي بيانات العينة المُقدمة:

ملاحظة:	\(X\)
1	2
2	3
3	4
4	3
5	3
6	2
7	3
8	4
9	5
10	3
11	2
12	3
13	1
14	2
15	3
16	4
17	5
18	6
19	3
20	2
21	4
22	5
23	6
24	10
25	10
26	10
27	12
28	12
29	1
30	2
31	3
32	3
33	23

يجب حساب الترددات النظرية \(f_i\) بالإضافة إلى الدرجات Z المرتبطة بها \(z_i\), لـ \(i = 1, 2, ..., 33\):

لاحظ أن الترددات النظرية \(f_i\) يتم تقريبها باستخدام الصيغة التالية:

\[ f_i = \frac{i - 0.375}{n + 0.25} \]

حيث \(i\) يُطابق الموضع في مجموعة البيانات المُرتبة, و\(z_i\) هو الدرجة المعيارية المُقابلة. يُحسب هذا على النحو التالي:

\[ z_i = \Phi^{-1}(f_i)\]

تم الحصول على الجدول التالي

الموضع (i)	X (ترتيب تصاعدي)	ف أنا	ز أنا
1	1	0.0188	-2.079
2	1	0.0489	-1.656
3	2	0.0789	-1.412
4	2	0.109	-1.232
5	2	0.1391	-1.084
6	2	0.1692	-0.957
7	2	0.1992	-0.844
8	2	0.2293	-0.741
9	3	0.2594	-0.645
10	3	0.2895	-0.555
11	3	0.3195	-0.469
12	3	0.3496	-0.386
13	3	0.3797	-0.306
14	3	0.4098	-0.228
15	3	0.4398	-0.151
16	3	0.4699	-0.075
17	3	0.5	0
18	3	0.5301	0.075
19	4	0.5602	0.151
20	4	0.5902	0.228
21	4	0.6203	0.306
22	4	0.6504	0.386
23	5	0.6805	0.469
24	5	0.7105	0.555
25	5	0.7406	0.645
26	6	0.7707	0.741
27	6	0.8008	0.844
28	10	0.8308	0.957
29	10	0.8609	1.084
30	10	0.891	1.232
31	12	0.9211	1.412
32	12	0.9511	1.656
33	23	0.9812	2.079

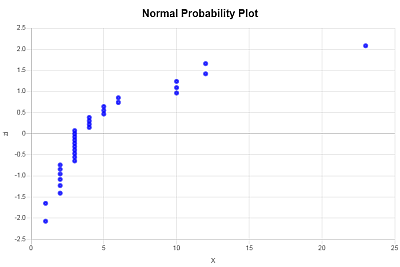
يتم الحصول على مخطط الاحتمالية الطبيعية برسم قيم X (بيانات العينة) على المحور الأفقي, وقيم \(z_i\) المقابلة على المحور الرأسي. ويتم الحصول على مخطط الاحتمالية الطبيعية التالي: