Statistiques Tutoriels

Tutoriel ANOVA

Dans le tutoriel de cette semaine, nous allons couvrir le sujet de Analyser la variance . Voir ci-dessous une liste d'exemples de problèmes pertinents, avec des solutions étape sy étape.

Nous espérons que vous les trouverez utiles. Nous partageons des tutoriels complets, des astuces et des astuces avec les membres de notre communauté. N'hésitez pas à Nous contacter si vous avez des questions.

Exemples de problèmes ANOVA

Question 1: Une analyse de la variance a été utilisée pour évaluer les différences moyennes à partir de mesures répétées Étude de recherche. Les résultats ont été rapportés comme F (3,24) = 6,40.

une. Combien de conditions de traitement ont été comparées dans l'étude?

b. Combien de personnes ont participé à l'étude?

Solution: (a) Il y avait 3 + 1 = 4 conditions de traitement.

(b) Le nombre total d'individus est de 3 + 24 + 1 = 28.

Question 2: Les données suivantes représentent les résultats d'une étude à mesures indépendantes comparant trois traitements.

une. Calculez SS pour l'ensemble de 3 moyens de traitement. (Utilisez les trois moyennes comme un ensemble de scores n = 3 et calculez SS.)

b. En utilisant le résultat de la partie a, calculez n (SSmeans). Notez que cette valeur est égale à SS entre (voir l'équation 13.6).

c. Maintenant, calculez SS entre avec la formule de calcul en utilisant les valeurs T (équation 13.7). Vous devez obtenir le même résultat que dans la partie b.

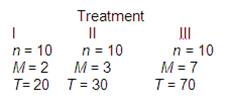
Solution: (a) Nous obtenons que \(\bar{M}=\frac{2+3+7}{3}=4\)

ce qui signifie que

\[S{{S}_{Means}}={{\left( 2-4 \right)}^{2}}+{{\left( 3-4 \right)}^{2}}+{{\left( 7-4 \right)}^{2}}=4+1+9=14\]

(b) Cela implique que \(n*S{{S}_{Means}}=10\times 14=140\).

\[S{{S}_{Between}}=\frac{{{20}^{2}}}{10}+\frac{{{30}^{2}}}{10}+\frac{{{70}^{2}}}{10}-\frac{{{120}^{2}}}{30}=140\]

Question 3: Les dommages aux maisons présentent par une tuyauterie éclatée peuvent être coûteux à réparer. Au moment où la fuite est découverte, des centaines de gallons d'eau ont peut-être déjà inondé la maison. Les vannes d'arrêt automatiques peuvent empêcher les dégâts d'eau importants dus à des pannes de plomberie. Les vannes contiennent des capteurs qui coupent le débit d'eau en cas de fuite, évitant ainsi les inondations. Une caractéristique importante est le temps (en millisecondes) nécessaire au capteur pour détecter la fuite d'eau. Les données d’échantillon obtenues pour quatre vannes d’arrêt sont différentes dans le fichier Waterflow.

une. Produire la table ANOVA appropriée et effectuer un test d'hypothèse pour déterminer si le temps de détection moyen diffère entre les quatre modèles de vannes d'arrêt. Utilisez un niveau de signification de 0,05.
b. Quelle est la source de variation entre les échantillons?

Vanne 1	Vanne 2	Vanne 3	Vanne 4
17	18	28	17
dix	17	25	17
18	11	30	17
18	16	26	19
17	16	25	18
14	18	27	21
18	14	23	21
13	17	23	12
dix	20	26	15
11	14	22	18

Solution: Le tableau suivant est obtenu à partir des données fournies

Obs.	Vanne 1	Vanne 2	Vanne 3	Vanne 4
	17	18	28	17
	dix	17	25	17
	18	11	30	17
	18	16	26	19
	17	16	25	18
	14	18	27	21
	18	14	23	21
	13	17	23	12
	dix	20	26	15
	11	14	22	18

Signifier	14,6	16,1	25,5	17,5
St. Dev.	3.406	2,558	2.461	2.677

Nous aimerions tester

\[H_0: \,\mu_{1}= \mu_{2}= \mu_{3}= \mu_{4}\]

\[H_A: \operatorname{Not all the means are equal}\]

Avec les données du tableau ci-dessus, nous pouvons calculer les valeurs suivantes, qui sont nécessaires pour construire la table ANOVA. Nous avons:

\[SS_{Between}=\sum\limits_{i=1}^{k}{n}_{i} {\left( {\bar{x}}_{i}-\bar{\bar{x}} \right)}^{2}\]

and therefore

\[SS_{Between}={10}\left({14.6}-{18.425}\right)^2+ {10}\left({16.1}-{18.425}\right)^2+ {10}\left({25.5}-{18.425}\right)^2+ {10}\left({17.5}-{18.425}\right)^2=709.475\]

Also,

\[SS_{Within} = \sum\limits_{i=1}^{k}{\left( {n}_{i}-1 \right) s_{i}^{2}}\]

d'où nous tirons

\[SS_{Within}=\left({10}-1\right) \times {3.406}^2+ \left({10}-1\right) \times {2.558}^2+ \left({10}-1\right) \times {2.461}^2+ \left({10}-1\right) \times {2.677}^2=282.3\]

Therefore

\[MS_{Between}=\frac{SS_{Between}}{k-1}= \frac{{709.475}}{3}= {236.492}\]

De la même manière, on obtient que

\[MS_{Within} = \frac{SS_{Within}}{N-k}= \frac{{282.3}}{36}= {7.842}\]

Par conséquent, la statistique F est calculée comme suit:

\[F=\frac{MS_{Between}}{MS_{Within}} = \frac{{236.492}}{{7.842}}= {30.1583}\]

La valeur critique pour \(\alpha ={0.05}\), \(df_{1} = 3\) et \(df_{2}= {36}\) est donnée par

\[F_C = {2.8663}\]

et la valeur p correspondante est

\[p=\Pr \left( {{F}_{3,36}}> {30.1583} \right) = {0.000}\]

On observe que la valeur p est inférieure au niveau de signification \[\alpha =0.05\], et par conséquent nous rejetons \({{H}_{0}}\). Par conséquent, nous avons suffisamment de preuves pour rejeter l'hypothèse nulle de moyennes égales, au niveau de signification de 0,05.

En résumé, nous avons le tableau ANOVA suivant: