多项式图表

如果你需要帮助绘制一个多项式函数的图形,请使用这个计算器。这个过程很简单：你只需输入你想要绘制的多项式函数。你可以写成'3x^3 + x - 1',或者你可以在前面加上函数名称,如'p(x) = 3x^3 + x - 1'。

提供的多项式的系数不一定是整数,可以是分数或任何有效的代数表达式。你提供的多项式可以简化或不简化,这并不重要。

然后,一旦提供了多项式,你可以选择确定将被绘制的x值的范围,然后你点击 "计算",不久,这个过程的所有步骤将被显示出来。

多项式函数 是你在代数和微积分中会发现的最重要的对象之一。此外,多项式导致了解决多项式方程的需要,这些方程在生活的各个方面都有大量的应用,甚至超越了数学。

多项式函数的基础知识

让我们回顾一下,一个多项式函数有以下形式。

\[\displaystyle p(x) = a_0 + a_1 x + a_2 x^2 + .... + a_n x^n \]

其中我们假设\(a_n \ne 0\),并且我们说 多项式的度数 在这种情况下,等于\(n\),前导系数是\(a_n\)。定义多项式的度数的通俗方法是,它对应于多项式表达式中存在的最高幂。

例如,\(p(x) = 3x^2 + 2x - 1\)是一个2度的多项式,它的前导系数是3。现在,\(p(x) = \sin(3x^2 + 2x - 1)\)不是一项多项式,例如。

如何做多项式图形？

多项式的作图原则上与其他函数的作图相同。如果你用手来做,你会把x和y的几个值列在表格里,然后你会描出一条曲线,或多或少会通过你表格里的点。

自然,这种方法有点原始,因为一般来说,我们不可能仅仅通过知道一堆我们所统计的点就一定知道一个函数的完整图形。

幸运的是,对于多项式来说,这个任务要简单一些,实际上我们只要知道它的前导系数和它的度数就可以知道很多关于它的图形。

多项式函数作图的步骤

多项式的图形最终取决于每个多项式的具体系数。但我们可以对多项式的最终行为和实根的存在做出一些强有力的陈述。

让我们回顾一下,多项式的终结行为是指当x非常大且为负数时,以及x非常大且为正数时,多项式的行为。

• 步骤1： 确定多项式函数,如果可以的话,将其简化,因为简化后的表达式更容易作图。
• 第2步： 你知道这个多项式的根吗？如果是实根,你就知道多项式与x轴相交的点,这给你提供了强有力的图形参考。
• 第 3 步： 如果多项式的度数是奇数,那么对于大的负x值和大的正x值,最终的行为将是相反的。如果前导系数是正的,对于大的负x值,多项式将是非常大的负值,而对于大的正x值,多项式将是非常大的正值。如果前导系数是负的,对于大的负x值,多项式将是非常大的和正的,而对于大的正x值,多项式将是非常大的和负的。
• 第4步： 如果多项式的度数是偶数,那么对于大的负x值和大的正x值,最终的行为将是一样的。如果前导系数是正的,对于大的负x值和正x值,多项式将是非常大的正值。如果前导系数为负数,对于大的负数和正数的x值,多项式将是非常大的负数。
• 第 5 步： 如果多项式的度数是奇数,那么多项式将至少穿过一次x轴（所以它至少有一个实根）,而对于偶数度数,多项式不一定会穿过x轴。
• 第6步。 一个n度的多项式最多可以穿越x轴n次。例如,一个4度的多项式最多可以穿越x轴4次

因此,举例来说,一个立方体多项式最多可以穿过X轴3次,但不一定非得如此。

图形计算器

使用图形计算器的优点是什么？很多。这并不是说,能够用纸笔准确地画出多项式的草图就不是一项好的技能。

\[\displaystyle \frac{a}{b} \times \frac{c}{d} = \displaystyle \frac{ac}{bd} \]

• 优势1。 你要确保你得到的是对多项式的实际图形的准确描述
• 优势2。 你可以用它来检查你自己的工作,以确保你是否遵循了正确的步骤。
• 优势3。 一个好的计算器会选择一个适当的窗口来显示图形的最相关方面

一个好的图形可以告诉你很多关于函数的特性,对于多项式也是如此。为多项式作图可以帮助你真正直观地了解多项式的根的类型。

技巧和窍门

要小心过度解读你在多项式图中看到的东西。你不可能轻易看出有多少倍数的根,所以没有什么可以代替实际的函数。

如果你想尝试其他类型的函数,可以试试这个 功能图 工具。

例子。给多项式函数作图

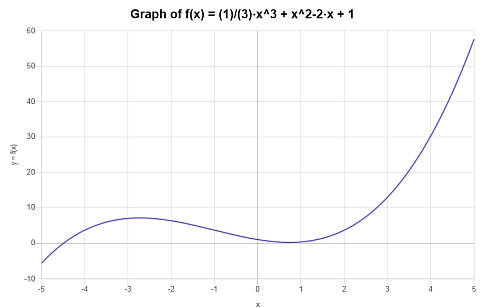
给下列多项式作图。\(p(x) = \frac{1}{3} x^3 + x^2- 2x +1 \)<

解决方案： 我们得到了以下需要计算的多项式表达式。\(\displaystyle \frac{1}{3} x^3 + x^2- 2x +1\)。

所提供的表达式是不可还原的,所以没有什么可以简化的。

在区间\([-5, 5]\)上,给定的多项式表达式可以得到如下图。

例子。多项式图表

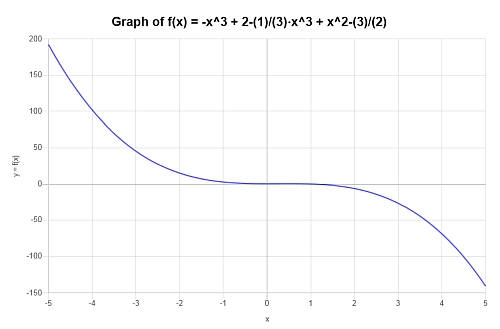
简化并作图。\(p(x) = x^4 - x^3 + 2 - \frac{1}{3}x^3 + x^2 - \frac{3}{2}\)的情况

解决方案： 现在,我们需要用。\(\displaystyle -x^3+2-\frac{1}{3}x^3+x^2-\frac{3}{2}\)。

可以得到以下简化结果。

这就结束了多项式简化的过程。

那么,在\(\displaystyle -\frac{4}{3}x^3+x^2+\frac{1}{2}\)的区间\([-5, 5]\)上,就会得到以下图。

例子。更多的多项式图形

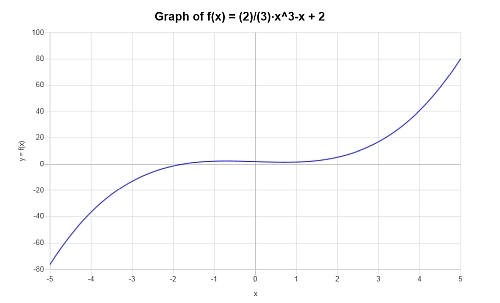
求下列多项式\( p(x) = \frac{2}{3} x^3 - x +2 \)的图形。

解决方案： 在这个例子中,所提供的多项式是。\(\displaystyle \frac{2}{3} x^3 - x +2 \)。

在这种情况下,所提供的表达式是不可还原的,所以没有什么可简化的。

在区间\([-5, 5]\)上,给定的多项式表达式可以得到如下图。

更多多项式计算器

给多项式作图是非常有用的,因为它向我们展示了它们在根周围的行为的主要特征以及它们的最终行为。绘制图形通常与确定根的大概位置同时进行,这可以用在 多项式的因式分解 也是如此。

尽管我们可以从图形中了解到很多关于多项式的信息,但我们仍然需要通过尝试 寻找有理根 作为一个新的起点。 解多项式方程 度数大于2的（这个,不属于 二次方程 ).

系统地猜测或寻找有理根,并配以使用 长期分工 或者 合成部 所以要用 因素定理 可能会导致成功搜索到 多项式根 ,但这种方法并不总是有效的,很多时候你需要依靠计算器来寻找数字近似值。