功能:它们是什么以及如何处理它们
函数的概念极其重要,在数学中绝对无所不在。这就是为什么我们需要好好复习一下,然后再尝试理解一些在深入研究微积分主题后会出现的好处,例如微分和积分。
什么是套装?
我们需要了解的第一个元素是 放 .集合只是元素的集合。那么,通过知道哪些元素属于该集合而哪些元素不属于该集合,可以非常简单地定义一个集合。这似乎是一项超级简单的任务,集合理论应该简单地简化为具有确定哪些元素属于集合的明确规则。
例如,让我们定义偶数集,我们称之为\(E\)。为什么它甚至是一个集合?因为它有一个明确的规则来确定哪些元素属于 \(E\):如果实数 \(x\) 可以被 2 整除,则它属于 \(E\)。该规则明确适用于每个单个实数,确定它是否属于 \(E\)。为什么我说“毫不含糊”并不断重复。因为它很重要。明确表示无法断定给定的 \(x\) 既属于又不属于 \(E\)。不幸的是,事情有时超出了我们的想象。与我们的直觉相反,一个可以用简单的归属规则定义的集合会导致一个模糊的(矛盾的)归属分类,正如伯特兰·罗素在他著名的悖论中所展示的那样。罗素表明应该使用更仔细的定义集合。
出于所有实际目的,我们将集合视为元素的集合,可由归属规则定义 .
什么是两套产品?
在上面给出的定义的上下文中,让 \(A\) 和 \(B\) 被设置。两个集合的乘积 \(A\times B\) 是另一个集合,它被定义为形式为 \(\left( a, b \right)\) 的所有可能有序对的集合,其中 \(a\) 属于 \(A\),而 \(b\) 属于 \(B\)。那么,\(A\times B\) 是一个集合,它的元素是 \(\left( a ,b \right)\) 形式的有序对。不要让那个符号给你留下深刻印象。当我说“形式为 \(\left( a, b \right)\) 的有序对”时,符号 \(\left( a, b \right)\) 是一个组合符号,表示由两个实体 \(a\) 和 \(b\) 组成的元素,并将第一个元素标识为 \(a\),将第二个元素标识为 \(b\) .就是这样。我们可以选择符号 \(a\_b\) 而不是 \(\left( a,b \right)\),它会正常工作。
你将不得不原谅我,但我必须写出两个集合的乘积的数学定义(我们也可以将集合相乘......你怎么看,我们只会停止数字,嗯?):
\(A\times B=\left\{ \left( a,b \right):\,\,\,a\in A,\,\,\,b\in B \right\}\)
我写这个定义的原因是让你看看它,并认识到我们使用非常紧凑的符号表达的方式与我在上面段落中用单词定义它的方式完全相同。我希望你能减轻对阅读数学陈述的恐惧。数学家有时可能是时髦的人,但他们确实找到了好的,明确的和紧凑的符号。因此,数学语言非常容易阅读。对?对?请告诉我我是对的...
旁注,由于历史原因,两个集合 \(A\times B\) 的乘积通常被称为 笛卡尔积 .
现在,函数的定义(最终)
好吧,我撒谎了,在定义函数之前还有一步。我们需要定义一个概念 关系 .什么是关系?除了作为英语单词的常见用法外,关系只是笛卡尔积的一个子集。笛卡尔积的任何子集都是一个关系。因此,如果 \(A\) 和 \(B\) 是集合,则集合 \(R\) 是一个关系如果 \(R\subseteq A\times B\)。由于任何集合都可以视为其自身的子集,因此所有笛卡尔积本身就是关系。
把它放在一个框架上:
关系是作为笛卡尔积的子集的集合
让我们得到更多的图形。考虑集合 \(A=\left[ 0,1 \right]\)(它是所有大于或等于 0 的实数,它们也小于或等于 1)。什么是笛卡尔积 \(A\times A\)?让我们模仿我们刚刚学到的东西。笛卡尔积 \(A\times A\) 是 \(\left[ 0,1 \right]\times \left[ 0,1 \right]\) 在这种情况下是所有对的集合 \(\left( x, y \right)\),其中 \(x\) 和 \(y\) 都属于 \(\left[ 0,1 \right]\)。笛卡尔积通常很容易绘制。看看下面的阴影区域:

现在,什么会建立关系?我们可以"雕刻"出我们想要的所有阴影区域,剩下的是 \(\left[ 0,1 \right]\times \left[ 0,1 \right]\) 中的关系。例如,我们可以剪掉"角落"以获得以下子区域:

上面的区域(集合)是一个关系。为什么?因为它是笛卡尔积 \(\left[ 0,1 \right]\times \left[ 0,1 \right]\) 的子集。但我们可以开拓更多。刻出四分之一圆怎么样?请参阅下面的区域。
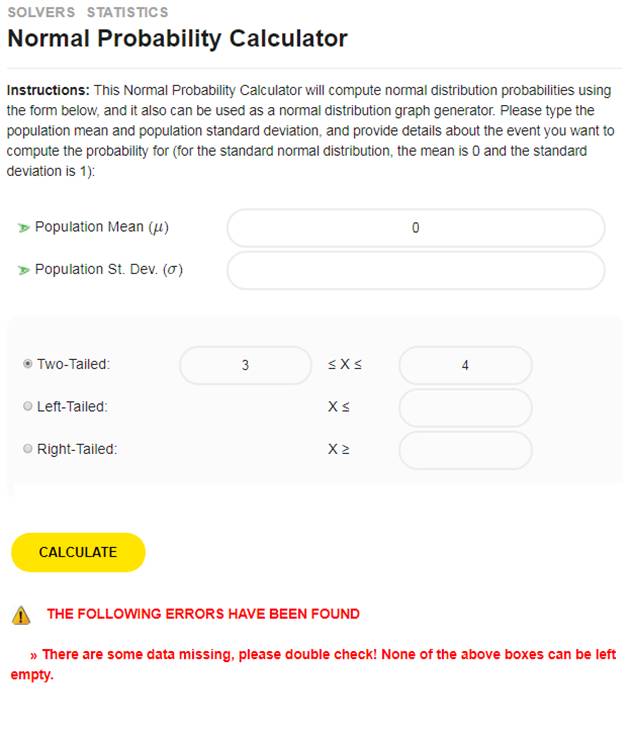
上面的区域(集合)是一个关系。为什么?同样,因为它是笛卡尔积 \(\left[ 0,1 \right]\times \left[ 0,1 \right]\) 的子集。
现在,让我举一个 \(\left[ -1,1 \right]\times \left[ -1,1 \right]\) 中两个关系的例子。见下图:
关系 1
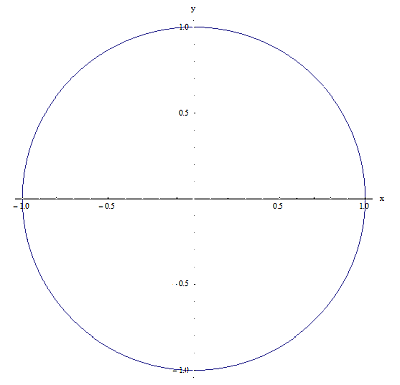
关系2
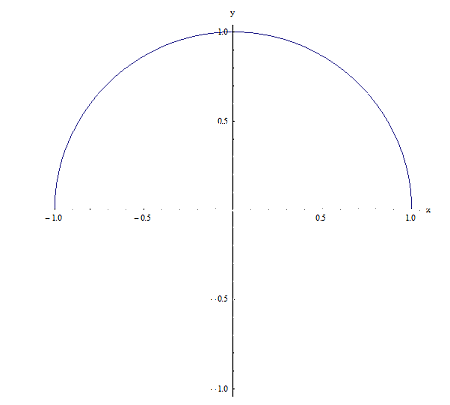
它们显然都是关系(因为它们都包含在笛卡尔积 \(\left[ -1,1 \right]\times \left[ -1,1 \right]\) 中,但它们有一个关键区别:对于关系 1,对于 \(\left[ -1,1 \right]\) 上的给定点 x,有两个点 \({{y}_{1}}\) 和 \({{y}_{2}}\),它们具有 \(\left( x,{{y}_{1}} \right)\) 和 \(\left( x,{{y}_{2}} \right)\) 属于到关系 1。例如,对于 x = 0,有两点 \({{y}_{1}}=1\) 和 \({{y}_{2}}=-1\) 使得 \(\left( 0,1 \right)\) 和 \(\left( 0,-1 \right)\) 属于关系 1。现在,对于关系 2,情况并非如此,因为例如,对于 x = 0,只有 \(y=1\)使点 \(\left( 0,1 \right)\) 属于关系 1。
最后我们可以定义一个函数:函数 \(R\) 是一个集合,它是一个关系,它还有一个性质,如果点 \(\left( x,y \right)\) 属于 \(R\),那么没有其他点 \(\bar{y}\) 不同于 \(y\) 具有 \(\left( x,\bar{y} \right)\) 属于 \(R\) 的性质以及。换句话说,一个函数是一个与额外要求的关系,即其域中的每个 \(x\) 只与一个 \(y\) 相关联。
如何知道如何区分函数和关系?
小工具!我们使用了一个叫做“垂直线测试”的小技巧:我们画了一条假想的垂直线,然后将它从左到右扫过一遍,然后在心智图中画出垂直线与关系相交的位置。
• 如果在任何一点,垂直线在多个点处与关系相交,则该关系未通过垂直线测试,则该关系不是函数
• 如果在任何一点,垂直线与关系的任何地方都不超过一个点,则该关系通过垂直线测试,则该关系是一个函数
请参阅以下两个示例:
示例 1:它未通过垂直线测试,因为图中所示的垂直线在多个点与关系相交:NOT A FUNCTION
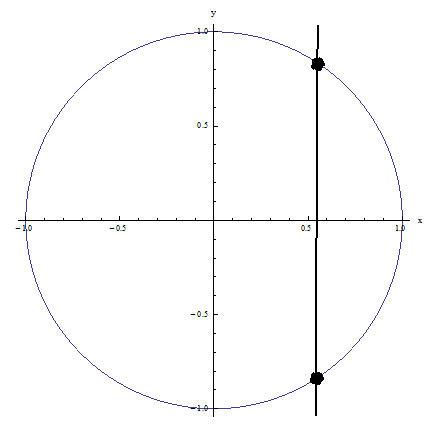
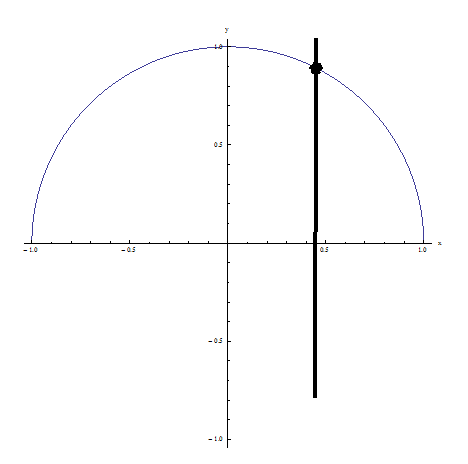
示例 2:它通过了垂直线测试,因为没有垂直线在多个点与关系相交:这是一个函数!
有许多图形应用程序可以通过函数进行,包括计算 水平渐近线 ,垂直渐近线和倾斜渐近线(如果适用)。
