多项式长除法计算器

这个计算器可以帮助你在两个给定的多项式之间进行长除法的过程。为此,你需要提供两个有效的多项式表达式。这些多项式可能已经简化或没有简化,如果需要的话,计算器会简化它们。

当 多项式的除法 你需要提供两个多项式,一个是你要除以的,称为分红,另一个是除数。

一旦你提供两个有效的 多项式 下一步是点击 "计算 "按钮,它将显示所提供的多项式之间所需的长除法的所有相应计算。

采用以下方法进行多项式除法的过程 长除法 这是一个相对简单的方法,但需要一个非常有组织的方法,以便不迷失方向。通常情况下,使用表格的方式来显示相应的步骤,效果最好。

一个更简单的方法是用 合成部 ,但这只适用于除数为1度的情况,所以它的范围比较有限

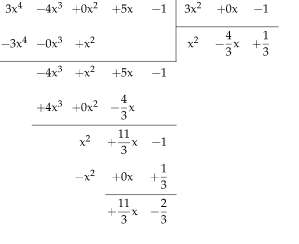
什么是多项式？

多项式是一种简单的表达式,它将某一变量x（或所选择的任何变量名称）的整数次方与和和减去,可能乘以常数。

例如,表达式\(p(x) = 2x^2 + x + 1\)是\(2x^2\),\(x\)和\(1\)的组合,加了x的幂（注意,1是x的幂,如\(x^0 = 1\)。

另一方面,\(f(x) = 2x^2 + \sin(x) + 1\)不是一个多项式,因为\(\sin(x)\)项不是x的幂。

多项式运算

多项式,很像数字,可以用以下方法操作 多项式的加,减,乘,除法 .加法和减法很简单,以一种非常直观的方式进行。例如,如果你有两个多项式,\(p(x) = 2x+1\)和\(q(x) = x^3 + 2x+ 3\),添加多项式是通过字面上添加项来实现的,如

\[p(x) + q(x) = 2x + 1 + x^3 + 2x+ 3 = x^3 + 4x + 4\]

对于减法,你还要减去被减的多项式的相应项。例如,如果你有两个多项式,\(p(x) = 2x+1\)和\(q(x) = x^3 + 2x+ 3\),那么,做减法的方法如下

\[p(x) - q(x) = 2x + 1 - (x^3 + 2x+ 3) = 2x + 1 - x^3 - 2x - 3) = -x^3 -2\]

乘法就比较复杂了,因为你必须使用分配属性进行交叉乘法。

\[p(x) \cdot q(x) = (2x + 1) \cdot (x^3 + 2x+ 3) = 2x \cdot x^3 + 2x \cdot 2x + 2x \cdot 3 + 1\cdot x^3 + 1\cdot1 2x+ 1\cdot 3 = 2x^4 +x^3+4x^2+8x+3\]

除法稍微复杂一些,因为它涉及到一个多项式可能不除以的概念 正是 另一个多项式。在数学上,当我们有两个多项式\(p(x)\)和\(s(x)\)时,我们想用\(p(x)\)除以\(s(x)\),我们要找一个商\(q(x)\)和一个余数\(r(x)\)（都是多项式）,它们的特性是\(p(x)= q(x)\cdot s(x) + r(x)\),条件是 多项式的度数 \(r(x)\)小于\(s(x)\)的程度。这通常被称为 欧几里德分解法 .

长除法的方法

所以,长除法是一种系统的方法,从我们要除掉的两个多项式\(p(x)\)和\(s(x)\)开始,我们找到商\(q(x)\)和余数\(r(x)\),这样就可以

\[p(x)= q(x)\cdot s(x) + r(x)\]

这个算法非常有用,虽然这个问题看起来很简单,但如果不使用系统的方法,就不难迷失方向,保证能得出需要的商和余数。

做长除法的步骤是什么？

• 步骤1： 确定你要除掉的两个多项式p(x)和s(x),并确定p(x)为分母,s(x)为除数。
• 第2步： 检查红利p(x)的度数和s(x)的度数。如果s(x)的度数大于p(x)的度数,则余数就是红利p(x)本身,而商为零：q(x)=0,你就完成了
• 第 3 步： 在这种情况下,我们假设除数p(x)的度数大于或等于除数s(x)的度数,否则,我们将在第2步停止。
• 第4步： 我们需要进行一个寻找临时余数的迭代过程,直到我们到达余数的度数小于s(x)的度数。
• 第 5 步： 每次更新临时余数时,首先要找到当前临时余数的最高项与除数s(x)之间的比率。这个比率（是一个幂项）再乘以s(x),这个乘法的结果从当前的临时余数中减去,从而得到一个更新的余数
• 第6步。 这个过程一直持续到余数的度数低于s(x)的度数。在迭代的每一步中,临时余数的度数至少减少1,所以这个过程保证会结束

最后,在这个过程中 两次多项式的除法 被简化为计算乘法是多项式的和,这几乎是数字的情况。多项式的长除法是我们将数字除法的方式扩展到多项式。

长除法与寻找多项式方程的根有什么联系？

假设p(x)是你要除的红利,s(x)是被除数。根据长除法的方法,你将能够找到商q(x)和余数r(x),这样就可以了。

\[\displaystyle p(x) = q(x)s(x) + r(x) \]

但有时,会发生余数为r(x)=0的情况,在这种情况下,我们说s(x)除以p(x)（或它正好除以p(x)）。所以,当r(x)=0时

\[\displaystyle p(x) = q(x)s(x) \]

这表明,为了找到p(x)=0的根,我们可以分别得到解q(x)=0和s(x)=0,这两个方程的解比较简单。

这个长除法计算器的优点

正如我之前提到的,长除法并不难,但它确实需要一个系统的方法。使用一个巨大的优势是 除法计算器 像这样,你会得到这个过程的所有步骤。

自己知道如何进行步骤可能并不重要,但这个计算器可以让你看到它是如何完成的,每一步都有解释,消除了从数字计算器中得到余数和商的神秘感,比如数字计算器会给你答案而不显示步骤。

一个有步骤显示所有工作的长除法计算器可以确保你对计算的情况有一个清晰的认识。

例子。计算多项式的除法

计算以下多项式的除法。\(p(x) = \frac{1}{3} x^3 + \frac{5}{4}x - \frac{5}{6}\)和\(s(x) = x+3\)。

解决方案： 已经提供了以下多项式。\(\displaystyle p(x) = \frac{1}{3}x^3+\frac{5}{4}x-\frac{5}{6}\),需要除以多项式\(\displaystyle s(x) = x+3\)。

请注意,红利的度数是\(\displaystyle deg(p) = 3\),而除数的度数是\(\displaystyle deg(s)) = 1\)。

步骤1： 红利\(\displaystyle p(x) = \frac{1}{3}x^3+\frac{5}{4}x-\frac{5}{6}\)的前导项是\(\displaystyle \frac{1}{3}x^3\),而除数\(\displaystyle s(x) = x+3\)的前导项则等于\(\displaystyle x\)。

因此,我们需要乘以\(x\)以得到红利的前导项是\(\displaystyle \frac{ \frac{1}{3}x^3}{ x} = \frac{1}{3}x^2\),所以我们把这个项加到商中。另外,我们用它乘以除数,得到\(\displaystyle \frac{1}{3}x^2 \cdot \left(x+3\right) = \frac{1}{3}x^3+x^2\),我们需要把它减去红利。

\[\begin{array}{rcccc} &\displaystyle \frac{1}{3}x^2 & \displaystyle & \displaystyle &\\[0.8em] \hline x+3\,) & \displaystyle \frac{1}{3}x^3 & \displaystyle & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle -\frac{1}{3}x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \end{array}\]

第2步： 在这种情况下,当前余数\(\displaystyle -x^2+\frac{5}{4}x-\frac{5}{6}\)的前导项是\(\displaystyle -1x^2\),而我们知道除数的前导项是\(\displaystyle x\)。

那么,我们需要乘以\(x\)来得到当前余数的前导项是\(\displaystyle \frac{ -1x^2}{ x} = -x\),所以我们把这个项加到商中。另外,我们用它乘以除数,得到\(\displaystyle -x \cdot \left(x+3\right) = -x^2-3x\),我们需要减去当前的余数。

\[\begin{array}{rcccc} &\displaystyle \frac{1}{3}x^2 & \displaystyle -x & \displaystyle &\\[0.8em] \hline x+3\,) & \displaystyle \frac{1}{3}x^3 & \displaystyle & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle -\frac{1}{3}x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle +3x & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle \frac{17}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \end{array}\]

第 3 步： 在这种情况下,当前余数\(\displaystyle \frac{17}{4}x-\frac{5}{6}\)的前导项是\(\displaystyle \frac{17}{4}x\),而我们知道除数的前导项是\(\displaystyle x\)。

那么,我们需要乘以\(x\)来得到当前余数的前导项是\(\displaystyle \frac{ \frac{17}{4}x}{ x} = \frac{17}{4}\),所以我们把这个项加到商中。另外,我们用它乘以除数,得到\(\displaystyle \frac{17}{4} \cdot \left(x+3\right) = \frac{17}{4}x+\frac{51}{4}\),我们需要减去当前的余数。

\[\begin{array}{rcccc} &\displaystyle \frac{1}{3}x^2 & \displaystyle -x & \displaystyle +\frac{17}{4}&\\[0.8em] \hline x+3\,) & \displaystyle \frac{1}{3}x^3 & \displaystyle & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle -\frac{1}{3}x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle +3x & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle \frac{17}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle & \displaystyle & \displaystyle -\frac{17}{4}x & \displaystyle -\frac{51}{4}\\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle & \displaystyle -\frac{163}{12}\\[0.8em] \end{array}\]

计算结束,因为当前余数\(r(x) = -\frac{163}{12}\)的度数小于除数\(s(x) = x+3\)的度数。

结论。 Therefore, we conclude that for the given dividend \(\displaystyle p(x) = \frac{1}{3}x^3+\frac{5}{4}x-\frac{5}{6}\) and divisor \(\displaystyle s(x) = x+3\), we get that the quotient is \(\displaystyle q(x) = \frac{1}{3}x^2-x+\frac{17}{4}\) and the remainder is \(\displaystyle r(x) = -\frac{163}{12}\), and that