Рациональные функции

Этот калькулятор рациональных функций позволит вам проанализировать наиболее важные точки предоставленной вами рациональной функции со всеми показанными шагами. Обычно для большинства рациональных функций можно найти точки пересечения, вертикальные асимптоты и ее график. Некоторые конкретные рациональные функции также будут иметь горизонтальные асимптоты.

Тип функции, которую вы можете предоставить, похож на 'f(x)=1/x - x' или что-то, включающее полиномы более высокой степени, например 'f(x) = (x^3-1)/(x^2+x )'

После того, как будет предоставлена действительная рациональная функция, вы можете нажать кнопку "Рассчитать", и вы получите все показанные для вас шаги.

Одним из основных свойств рациональной функции является то, что вы можете свести ее вычисление к задаче решение полиномиальных уравнений , который является одним из "простейших" типов уравнения, которые вы можете решить .

Что такое рациональная функция

Рациональная функция – это функция, включающая в себя частное двух многочленов \(P(x)\) и \(Q(x)\), где делитель \(Q(x)\) не равен нулевому многочлену. Тогда формула рациональной функции имеет вид

\[\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} \]

Например, функция

\[\displaystyle f(x) = \displaystyle \frac{x^2-1}{x+1} \]

является рациональной функцией, потому что это в точности частное двух многочленов. Но например

\[\displaystyle g(x) = \displaystyle \frac{x^2+1}{\sin x} \]

нерационально, поскольку делитель не является многочленом. Заметьте: когда мы говорим, что делитель \(Q(x)\) не равен нулевому многочлену, мы НЕ говорим, что \(Q(x)\) не может иметь нулей. Например, в данном случае \(\displaystyle f(x) = \displaystyle \frac{x^2-1}{x+1} \) делителем является \(Q(x) = x + 1\), который имеет один ноль в позиции \(x = -1\).

Чего мы не хотим, так это чего-то вроде

\[\displaystyle g(x) = \displaystyle \frac{x^2+1}{0} \]

потому что, хотя в этом случае \(Q(x) = 0\) технически является полиномом, это нулевой полином (который везде равен нулю).

Шаги по вычислению рациональной функции

• Шаг 1: Во-первых, убедитесь, что у вас есть рациональная функция, для которой вы можете определить числитель P(x) и знаменатель Q(x)
• Шаг 2: Если вы не находите строго описанную выше структуру, вы останавливаетесь. Возможно, вам придется сгруппировать термины с помощью алгебраические сокращения .
• Шаг 3: Вам нужно найти действительные нули P(x) и Q(x), если таковые имеются. Найденные выводы будут тесно связаны с нулями как P(x), так и Q(x)
• Шаг 4: Чтобы найти точку пересечения по оси Y, вы оцениваете функцию в нуле, вычисляя f(0). Пересечение оси y будет корректно определено, если x = 0 не является нулем Q(x)
• Шаг 5: Чтобы найти точки пересечения с x, вы получаете нули P(x), которые не являются нулями Q(x)
• Шаг 6: Для нахождения вертикальных асимптот вам необходимо найти нули Q(x), которые не являются нулями P(x)
• Шаг 7: Для нахождения горизонтальных асимптот необходимо, чтобы степень Q(x) была больше или равна степени P(x)

Заметьте, что, как и ожидалось, анализ рациональной функции зависит от Нахождение нулей многочлена , а затем собрать все выводы воедино. .

Обратите внимание, что областью определения рациональной функции является вся действительная линия, за исключением нулей делителя Q(x). Если существует нуль Q(x), который также является нулем P(x), то разрыв можно устранить. Диапазон рациональной функции будет зависеть от степеней P(x) и Q(x).

Зачем использовать рациональные функции

Рациональные функции используются потому, что они являются естественными расширениями полиномов. Их можно рассматривать как следующий шаг в сложности функции. Как мы знаем, полиномиальные выражения являются одними из самых простых функций, которые мы можем найти, но, тем не менее, они также являются одними из самых полезных.

Рациональные уравнения обычно встречаются в более сложных задачах смешивания, и тем не менее, с ними на удивление легко справиться, при условии, что используемые полиномы достаточно просты. Мы знаем как решать квадратные уравнения , но для полиномов степени 3 и выше дела обстоят сложнее.

Являются ли полиномиальные функции рациональными функциями?

Да, если P(x) — многочлен, то P(x) также рационален, потому что мы можем написать:

\[\displaystyle f(x) = \displaystyle \frac{P(x)}{1} \]

и Q(x) = 1 — реальный полином. Наоборот неверно: рациональная функция не обязательно является полиномом. Почему это? Потому что, естественно, если только Q(x) = 1, всякий раз, когда у вас есть \(\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} \), вы не будете уверены, что все члены будут свободными членами, как того требует определение многочлена.

Более формально, используя Теорема Об Остатке , у нас есть

\[\displaystyle f(x) = \displaystyle \frac{P(x)}{Q(x)} = d(x) + \frac{r(x)}{Q(x)}\]

где \(d(x)\) — полином, а \frac{r(x)}{Q(x)} — нет, поскольку степень r(x) ниже степени Q(x).

Пример. работа с рациональными функциями

Найдите точки пересечения, асимптоты и график: \(f(x) = \frac{x^2-1}{x+1}\)

Решение:

Нам была предоставлена следующая функция:

\[f\left(x\right)=\frac{x^2-1}{x+1}\]

Нам нужно найти точки пересечения и асимптоты, если они есть. После этого будет представлен график функции.

Найдем нули данной функции. Нам необходимо решить следующее рациональное уравнение:

\[\frac{x^2-1}{x+1}=0\]

Обратите внимание, что для \(x \ne -1\) мы можем упростить так:

\[\frac{x^2-1}{x+1} = 0 \Rightarrow \frac{(x-1)(x+1)}{x+1} = 0 \Rightarrow x-1 = 0\]

Вспомогательное уравнение числителя

Теперь приравняем числитель нулю и найдем решения. Тогда решениями рационального уравнения будут те корни, которые не приводят знаменатель к нулю.

Чтобы найти корни числителя, необходимо решить следующую задачу: \(x^2-1=0\)

Для квадратного уравнения вида \(a x^2 + bx + c = 0\) корни вычисляются по следующей формуле:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

В этом случае нам нужно решить уравнение \(\displaystyle x^2-1 = 0\), что означает, что соответствующие коэффициенты:

\[a = 1\] \[b = 0\] \[c = -1\]

Сначала мы вычислим дискриминант, чтобы оценить природу корней. Дискриминант вычисляется как:

\[\Delta = b^2 - 4ac = \displaystyle \left( 0\right)^2 - 4 \cdot \left(1\right)\cdot \left(-1\right) = 4\]

Поскольку в этом случае мы получаем дискриминант \(\Delta = \displaystyle 4 > 0\), который является положительным, мы знаем, что уравнение имеет два разных действительных корня.

Теперь, подставляя эти значения в формулу для корней, получаем:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{0 \pm \sqrt{\left(0\right)^2-4\left(1\right)\left(-1\right)}}{2\cdot 1} = \displaystyle \frac{0 \pm \sqrt{4}}{2}\]

итак, мы выяснили, что:

\[ {x}_1 = \frac{0}{2}-\frac{1}{2}\sqrt{4}=\frac{0}{2}-1=-1 \] \[{x}_2 = \frac{0}{2}+\frac{1}{2}\sqrt{4}=\frac{0}{2}+1=1\]

Вспомогательное уравнение знаменателя

Нам нужно найти корни знаменателя: \(x+1=0\)

Следовательно, решение \(x\) для данного линейного уравнения приводит к \(x=-1\).

Нули в числителе и знаменателе

На основе анализа, показанного выше, действительные нули числителя данной рациональной функции — это \( x_{ 1} = -1\) и \( x_{ 2} = 1\).

Также обнаружено, что в знаменателе есть один действительный ноль, то есть \( x_{ 1} = -1\).

Поиск x-перехватов

Основываясь на нулях числителя, которые не являются нулями знаменателя, мы обнаруживаем, что существует один перехват x, который равен \(\left(1, 0\right)\).

Поиск y-перехватов

Оценивая функцию \(x = 0\), мы обнаруживаем, что:

\[ f(0) = \frac{0^2-1}{0+1} = -1\]

тогда пересечение оси y будет \( \left(0, -1\right)\).

Вертикальные асимптоты

После анализа нулей делается вывод, что функция не имеет вертикальных асимптот.

Горизонтальные асимптоты

Обратите внимание, что степень числителя равна \(2\), а степень знаменателя — \(1\), а затем, поскольку степень многочлена в числителе превышает степень многочлена в знаменателе, мы заключаем, что горизонтальной линии не существует. асимптота.

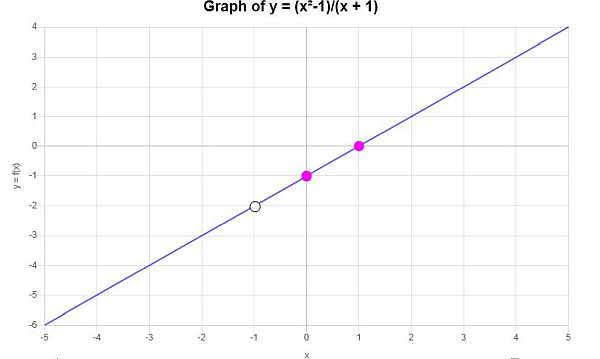
Получается следующий график:

Пример: горизонтальные асимптоты

Имеет ли эта рациональная функция горизонтальную асимптоту: \(f(x) = \frac{x^2-1}{x^2+1}\)?

Решение: Очевидно, что в этом случае функция состоит из частного двух многочленов, и оба они имеют степень, равную 2. То есть они имеют одинаковую степень и, следовательно, существует горизонтальная асимптота.

Мы также можем увидеть это, используя ограничения:

\[\lim_{x\to +\infty} f(x) = \lim_{x\to +\infty}\frac{x^2-1}{x^2+1} = \lim_{x\to +\infty}\frac{1-\frac{1}{x^2}}{1+\frac{1}{x^2}} = 1\]

из чего следует, что горизонтальная асимптота равна \(y = 1\). На этом расчет завершается.

Полезные калькуляторы функций

Функции — это фундаментальные математические объекты, которые инкапсулируют отношения между различными переменными. Используя Функциональный калькулятор может помочь вам систематически работать с функциями, которые могут оказаться слишком сложными для выполнения вручную.

Построение графиков рациональных функций является одним из наиболее распространенных игрушечных примеров, которые студенты изучают по алгебре и исчислению, и хотя, возможно, рациональные функции сами по себе не так часто встречаются в приложениях, аналитические навыки, необходимые для работы с ними, могут оказаться неоценимыми

То же самое касается Решение рациональных уравнений , где принципы манипулирования алгебраическими выражениями и сведения их к более низким членам будут чрезвычайно мощными для достижения более продвинутых навыков.

Теперь, если мы говорим о функции, мы не можем забыть вычисление производной функции , интегрирование и другие более продвинутые методы бесконечно малых величин.