Нули полинома

Этот калькулятор позволит вам вычислить полиномиальные корни любого действительного многочлена, который вы предоставите. Этот многочлен может быть любым многочленом степени 1 или выше.

Например, вы можете предоставить кубический многочлен, такой как p(x) = x^3 + 2x^2 - x + 1, или вы можете предоставить многочлен с нецелыми коэффициентами, такой как p(x) = x^3 - 13/12 x^2 + 3/8 x - 1/24.

После того, как вы предоставили калькулятору действительный многочлен, для которого вы хотите вычислить его корни, вы можете нажать кнопку "Вычислить", и вы увидите пошаговое выполнение процесса.

Необходимо отметить, что в процессе используются только элементарные методы, применяемые для нахождения корней, к которым относятся Теорема о рациональном нуле и Полиномиальное деление , а также с помощью квадратичная формула когда это необходимо.

Не существует общего метода, позволяющего найти ВСЕ корни для ВСЕХ возможных многочленов от степень больше 5, поэтому данный калькулятор будет находить только те корни, которые можно получить этими упомянутыми элементарными методами.

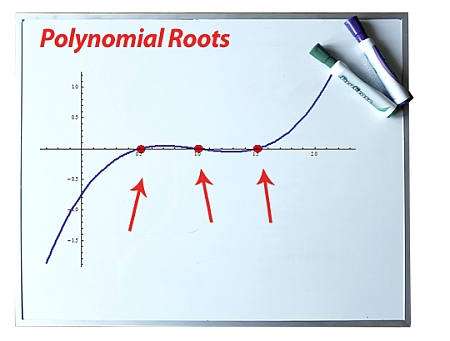
Что такое корень многочлена?

Учитывая полиномиальная функция \(p(x)\), мы говорим, что \(x\) является корнем многочлена, если:

\[\displaystyle p(x) = 0 \]

Говоря простым языком, корни многочлена - это точки, в которых функция многочлена \(p(x)\) пересекает ось x. Это хорошее представление, чтобы получить представление, но оно не совсем точное, потому что некоторые корни могут быть комплексными числами. Тогда вещественным корнем будет точка, в которой \(p(x)\).

Обратите внимание, что корни многочлена также называются нулями многочлена.

Каковы шаги для нахождения нулей многочлена?

• Шаг 1: Определите выражение, с которым вы хотите работать. Убедитесь, что оно является многочленом, и максимально упростите его
• Шаг 2: Мы будем использовать факторизация полиномов подход, чтобы найти его корень
• Шаг 3: Начните попытки найти элементарные (рациональные) корни с Теорема о рациональном нуле , и использовать Полиномиальное деление сократить исходный многочлен, если это возможно
• Шаг 4: Если шаг 3 сработал, и вы смогли сократить исходный многочлен, повторите предыдущие шаги, чтобы попытаться разложить сокращенный многочлен по коэффициентам

Обычно это нелегко, и это может потребовать больших вычислительных затрат, и это не гарантированно работает, но это лучший возможный подход, если мы ограничены использованием элементарных методов.

Является ли факторизация единственным способом нахождения корней

Не совсем, но все идет рука об руку. Сайт теорема факторов утверждает, что \(x - a\) является фактором многочлена \(p(x)\) тогда и только тогда, когда \(p(a) = 0\). Другими словами, корни и факторы тесно связаны.

Теперь, для полиномов степени 2 (это, квадратичные многочлены ) мы можем использовать явную формулу, которая хорошо известна квадратичная формула .

То же самое происходит для степеней 3 и 4, хотя формулы далеки от элементарных. Но для степеней 5 и выше такой формулы не существует - ключевой результат, доказанный Галуа и Абелем. Поэтому нет никакой надежды найти "общую формулу", и именно поэтому используется более мягкая формула полиномиальная факторизация подход.

Общие ошибки, которых следует избегать

Часто студенты расстраиваются из-за того, что не могут найти корни заданного числа полиномиальная функция , скажем \(p(x) = x^3+2 x^2-x+1 \), но они должны столкнуться с тем фактом, что не все многочлены можно решить с помощью элементарных инструментов.

Конечно, существует формула для решения \(x^3+2 x^2-x+1 = 0 \), но она не является элементарной, и не предполагается, что студенты будут ее знать.

Советы для успеха

Всегда старайтесь составить мысленную карту того, какой будет ваша стратегия: Запишите многочлен, который у вас есть, его степень, ведущий коэффициент и постоянный коэффициент.

Постройте график полинома если сможете, чтобы получить представление о его поведении. Есть ли очевидные факторизации, которые вы можете использовать? Используйте их. Всегда помните, что факторы = корни.

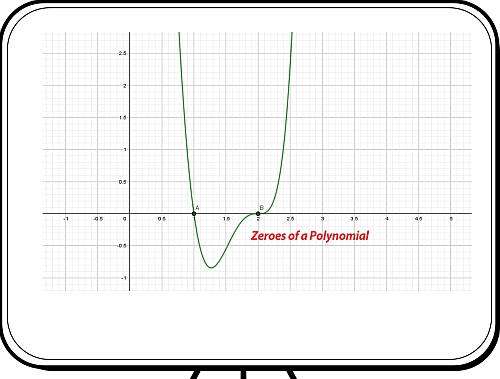
Пример: нули многочлена

Каковы нули в : \(x^5 + x^4 - x^3 + x^2 - x + 1\)?

Отвечать: Для данного примера нам предоставляется следующий многочлен: \(\displaystyle p(x) = x^5+x^4-x^3+x^2-x+1\). Для нахождения корней мы будем использовать метод факторизации.

Упрощение не требуется: Представленное полиномиальное выражение уже упрощено, поэтому нет необходимости упрощать его дальше.

Можно отметить, что степень представленного многочлена равна \(\displaystyle deg(p) = 5\). Также его ведущий коэффициент равен \(\displaystyle a_{5} = 1\), а постоянный коэффициент равен \(\displaystyle a_0 = 1\).

Теперь мы ищем целые числа, которые делят ведущий коэффициент \(a_{5}\) и постоянный коэффициент \(a_0\), который используется для поиска рациональных кандидатов.

▹ Разделителями \(a_{5} = 1\) являются: \(\pm 1\).

▹ Разделителями \(a_0 = 1\) являются: \(\pm 1\).

Поэтому, разделив все множители постоянного члена \(a_0 = 1\) на все делители \(a_{5} = 1\), мы получим следующий список потенциальных корней:

\[\pm \frac{ 1}{ 1}\]

Теперь необходимо оценить все потенциальные решения. Результаты, полученные при тестировании каждого кандидата, следующие:

\[\begin{array}{ccccclcc} x & = & \displaystyle -1 &:&    & \displaystyle \left(-1\right)^5+\left(-1\right)^4-\left(-1\right)^3+\left(-1\right)^2-\left(-1\right)+1 & = & \displaystyle 4 \ne 0 \\\\ x & = & \displaystyle 1 &:&    & \displaystyle 1^5+1^4-1^3+1^2-1+1 & = & \displaystyle 2 \ne 0 \\\\ \end{array}\]

Поскольку при ручной проверке не было выявлено рациональных корней, дальнейшее упрощение с помощью основных методов невозможно, и процесс заканчивается на этом шаге.

Вывод : В результате не было получено упрощение и не были определены корни многочлена с помощью основных методов

Пример: вычисление корней квадратичной функции

Вычислите решения: \(3x^2 - 2x - 4 = 0\).

Отвечать: Необходимо решить заданное квадратное уравнение \(\displaystyle 3x^2-2x-4=0\).

Корни квадратного уравнения вида \(a x^2 + bx + c = 0\) вычисляются с помощью следующего уравнения:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\]

В данном контексте уравнение, которое необходимо решить, имеет вид \(\displaystyle 3x^2-2x-4 = 0\), что указывает на соответствующие коэффициенты:

\[a = 3\] \[b = -2\] \[c = -4\]

Сначала мы определим природу корней, вычислив дискриминант. Дискриминант вычисляется следующим образом:

\[\Delta = b^2 - 4ac = \displaystyle \left( -2\right)^2 - 4 \cdot \left(3\right)\cdot \left(-4\right) = 52\]

Так как в данном случае дискриминант \(\Delta = \displaystyle 52 > 0\) положительный, то уравнение имеет два различных вещественных корня.

Отсюда получаем:

\[x = \displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a} = \displaystyle \frac{2 \pm \sqrt{\left(-2\right)^2-4\left(3\right)\left(-4\right)}}{2\cdot 3} = \displaystyle \frac{2 \pm \sqrt{52}}{6}\]

итак, мы выяснили, что:

\[ x_1 = \frac{2}{6}-\frac{1}{6}\sqrt{52}=\frac{2}{6}-\frac{1}{6}\cdot 2\sqrt{13}=\frac{2}{6}-\frac{1}{3}\sqrt{13}=\frac{1}{3}-\frac{1}{3}\sqrt{13} \] \[x_2 = \frac{2}{6}+\frac{1}{6}\sqrt{52}=\frac{2}{6}+\frac{1}{6}\cdot 2\sqrt{13}=\frac{2}{6}+\frac{1}{3}\sqrt{13}=\frac{1}{3}+\frac{1}{3}\sqrt{13}\]

Находим, что уравнение \( \displaystyle 3x^2-2x-4 = 0 \), имеет два вещественных корня, тогда:

\[\displaystyle 3x^2-2x-4 = 3 \left(x+\frac{1}{3}\sqrt{13}-\frac{1}{3}\right)\left(x-\frac{1}{3}\sqrt{13}-\frac{1}{3}\right)\]

поэтому исходный многочлен факторизуется как \(\displaystyle p(x) = 3x^2-2x-4 = 3 \left(x+\frac{1}{3}\sqrt{13}-\frac{1}{3}\right)\left(x-\frac{1}{3}\sqrt{13}-\frac{1}{3}\right) \), что завершает факторизацию.

Вывод : Таким образом, искомая факторизация имеет вид:

\[\displaystyle p(x) = 3x^2-2x-4 = 3 \left(x+\frac{1}{3}\sqrt{13}-\frac{1}{3}\right)\left(x-\frac{1}{3}\sqrt{13}-\frac{1}{3}\right)\]

Найдены корни \(-\frac{1}{3}\sqrt{13}+\frac{1}{3}\) и \(\frac{1}{3}\sqrt{13}+\frac{1}{3}\) .

Пример: нули полинома

Вычислите нули следующего многочлена: \(p(x)= x^3 - \frac{13}{12} x^2 + \frac{3}{8} x - \frac{1}{24} \).

Отвечать: Наконец, в данном примере мы имеем: \(\displaystyle p(x) = x^3-\frac{13}{12}x^2+\frac{3}{8}x-\frac{1}{24}\).

Первый Шаг: Данное многочленное выражение является неприводимым, поэтому упрощать нечего. Мы можем перейти к его факторизации.

Обратите внимание, что степень данного многочлена равна \(\displaystyle deg(p) = 3\), его ведущий коэффициент равен \(\displaystyle a_{3} = 1\), а постоянный коэффициент равен \(\displaystyle a_0 = -\frac{1}{24}\).

Рациональные Корни : Сначала мы попытаемся найти простые рациональные корни, используя теорему о рациональном нуле.

Следующая задача - найти целые числа, которые делят ведущий коэффициент \(a_{3}\) и постоянный коэффициент \(a_0\), которые будут использоваться для построения наших кандидатов в нули полиномиального уравнения.

Примечание: В этом случае мы видим, что для того, чтобы иметь как постоянный, так и ведущий коэффициент, необходимо усилить обе стороны уравнения на \(24\). Эквивалентное уравнение имеет вид:

\[24x^3-26x^2+9x-1 = 0\]

▹ Разделителями \(a_{3} = 24\) являются: \(\pm 1,\pm 2,\pm 3,\pm 4,\pm 6,\pm 8,\pm 12,\pm 24\).

▹ Разделителями \(a_0 = -1\) являются: \(\pm 1\).

Поэтому, разделив каждый делитель постоянного коэффициента \(a_0 = -1\) на каждый делитель ведущего коэффициента \(a_{3} = 24\), находим следующий список кандидатов в корни:

\[\pm \frac{ 1}{ 1},\pm \frac{ 1}{ 2},\pm \frac{ 1}{ 3},\pm \frac{ 1}{ 4},\pm \frac{ 1}{ 6},\pm \frac{ 1}{ 8},\pm \frac{ 1}{ 12},\pm \frac{ 1}{ 24}\]

Теперь необходимо протестировать всех кандидатов, чтобы понять, являются ли они решением. В результате тестирования каждого кандидата получено следующее:

\[\begin{array}{ccccclcc} x & = & \displaystyle -1 &:&    & \displaystyle 24\cdot \left(-1\right)^3-26\cdot \left(-1\right)^2+9\cdot \left(-1\right)-1 & = & \displaystyle -60 \ne 0 \\\\ x & = & \displaystyle 1 &:&    & \displaystyle 24\cdot 1^3-26\cdot 1^2+9\cdot 1-1 & = & \displaystyle 6 \ne 0 \\\\ x & = & \displaystyle -\frac{1}{2} &:&    & \displaystyle 24\left(\frac{-1}{2}\right)^3-26\left(\frac{-1}{2}\right)^2+9\left(-\frac{ 1}{ 2}\right)-1 & = & \displaystyle -15 \ne 0 \\\\ x & = & \displaystyle \frac{1}{2} &:&    & \displaystyle 24\left(\frac{1}{2}\right)^3-26\left(\frac{1}{2}\right)^2+9\cdot \frac{1}{2}-1 & = & \displaystyle 0 \\\\ x & = & \displaystyle -\frac{1}{3} &:&    & \displaystyle 24\left(\frac{-1}{3}\right)^3-26\left(\frac{-1}{3}\right)^2+9\left(-\frac{ 1}{ 3}\right)-1 & = & \displaystyle -\frac{70}{9} \ne 0 \\\\ x & = & \displaystyle \frac{1}{3} &:&    & \displaystyle 24\left(\frac{1}{3}\right)^3-26\left(\frac{1}{3}\right)^2+9\cdot \frac{1}{3}-1 & = & \displaystyle 0 \\\\ x & = & \displaystyle -\frac{1}{4} &:&    & \displaystyle 24\left(\frac{-1}{4}\right)^3-26\left(\frac{-1}{4}\right)^2+9\left(-\frac{ 1}{ 4}\right)-1 & = & \displaystyle -\frac{21}{4} \ne 0 \\\\ x & = & \displaystyle \frac{1}{4} &:&    & \displaystyle 24\left(\frac{1}{4}\right)^3-26\left(\frac{1}{4}\right)^2+9\cdot \frac{1}{4}-1 & = & \displaystyle 0 \\\\ x & = & \displaystyle -\frac{1}{6} &:&    & \displaystyle 24\left(\frac{-1}{6}\right)^3-26\left(\frac{-1}{6}\right)^2+9\left(-\frac{ 1}{ 6}\right)-1 & = & \displaystyle -\frac{10}{3} \ne 0 \\\\ x & = & \displaystyle \frac{1}{6} &:&    & \displaystyle 24\left(\frac{1}{6}\right)^3-26\left(\frac{1}{6}\right)^2+9\cdot \frac{1}{6}-1 & = & \displaystyle -\frac{1}{9} \ne 0 \\\\ x & = & \displaystyle -\frac{1}{8} &:&    & \displaystyle 24\left(\frac{-1}{8}\right)^3-26\left(\frac{-1}{8}\right)^2+9\left(-\frac{ 1}{ 8}\right)-1 & = & \displaystyle -\frac{165}{64} \ne 0 \\\\ x & = & \displaystyle \frac{1}{8} &:&    & \displaystyle 24\left(\frac{1}{8}\right)^3-26\left(\frac{1}{8}\right)^2+9\cdot \frac{1}{8}-1 & = & \displaystyle -\frac{15}{64} \ne 0 \\\\ x & = & \displaystyle -\frac{1}{12} &:&    & \displaystyle 24\left(\frac{-1}{12}\right)^3-26\left(\frac{-1}{12}\right)^2+9\left(-\frac{ 1}{ 12}\right)-1 & = & \displaystyle -\frac{35}{18} \ne 0 \\\\ x & = & \displaystyle \frac{1}{12} &:&    & \displaystyle 24\left(\frac{1}{12}\right)^3-26\left(\frac{1}{12}\right)^2+9\cdot \frac{1}{12}-1 & = & \displaystyle -\frac{5}{12} \ne 0 \\\\ x & = & \displaystyle -\frac{1}{24} &:&    & \displaystyle 24\left(\frac{-1}{24}\right)^3-26\left(\frac{-1}{24}\right)^2+9\left(-\frac{ 1}{ 24}\right)-1 & = & \displaystyle -\frac{91}{64} \ne 0 \\\\ x & = & \displaystyle \frac{1}{24} &:&    & \displaystyle 24\left(\frac{1}{24}\right)^3-26\left(\frac{1}{24}\right)^2+9\cdot \frac{1}{24}-1 & = & \displaystyle -\frac{385}{576} \ne 0 \\\\ \end{array}\]

Но так как мы нашли все искомые корни среди рациональных кандидатов, то находим, что \(\displaystyle x^3-\frac{13}{12}x^2+\frac{3}{8}x-\frac{1}{24} = \left(x-\frac{1}{2}\right)\left(x-\frac{1}{3}\right)\left(x-\frac{1}{4}\right) \), тогда:

\[\displaystyle p(x) = x^3-\frac{13}{12}x^2+\frac{3}{8}x-\frac{1}{24} = \left(x-\frac{1}{2}\right)\left(x-\frac{1}{3}\right)\left(x-\frac{1}{4}\right) \]

что завершает процесс факторизации.

Результат : Таким образом, окончательная факторизация имеет вид:

\[\displaystyle p(x) = x^3-\frac{13}{12}x^2+\frac{3}{8}x-\frac{1}{24} = \left(x-\frac{1}{2}\right)\left(x-\frac{1}{3}\right)\left(x-\frac{1}{4}\right)\]

Таким образом, найдены корни \(\frac{1}{2}\), \(\frac{1}{3}\) и \(\frac{1}{4}\).

Другие полезные калькуляторы полиномов

Нахождение нулей многочлена является одной из вершин алгебры, в той степени, в какой фундаментальная теорема алгебры говорит о существовании n корней для многочлена степени n. Эти корни не обязательно будут все вещественными, и некоторые из них (или все) могут быть комплексными числами.

В конечном счете, почти каждая задача в алгебре и исчислении может быть сведена к нахождению корней многочлена, включая решение полиномиальные уравнения например, такие, которые можно найти, например, при поиске пересечение между графами из \(y = x^2\) и \(y = x^3\).