Производный калькулятор
Инструкции: Используйте этот калькулятор производных для нахождения производной заданной вами функции, показывая все этапы процесса. Пожалуйста, введите функцию, для которой вы хотите вычислить производную, в поле ниже.
Производный калькулятор
Калькулятор производных проведет вас через все шаги и правила, используемые для нахождения производной заданной функции. Вы должны ввести функцию, например 3x + sin(x^2), или вы можете ввести определение всей функции, например f(x) = 3x^ 2 + 2tan(x^3).
Обратите внимание, что это можно назвать калькулятором первой производной, так же как и калькулятором производной. Первая производная и производная представляют собой одно и то же, и "первая" часть обычно опускается.
Функция может быть полностью упрощенной или нет, это не имеет значения, так как калькулятор сначала упростит функцию, если это необходимо, прежде чем вычислить ее производную.
Однажды действующая функция уже предоставлен, вам нужно просто нажать кнопку "Рассчитать", подождать несколько секунд, и вам будут представлены все этапы расчета.
Дифференциация является основным инструментом, используемым в исчислении (наряду с интегрированием), и это важная операция, которая широко используется в более продвинутой математике. Некоторые очень распространенные приложения включают расчет касательной , максимумы и минимумы и многое другое.
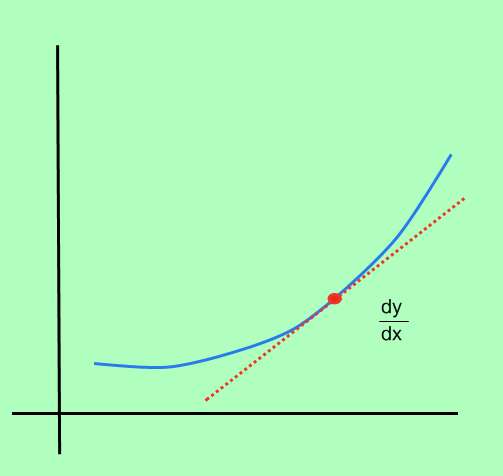
Как вычислить производную функции?
Процесс вычисления производной функции называется дифференциация и заключается в определении мгновенной скорости изменения точки, в каждой точке области функции.
Что такое мгновенная скорость изменения функции? Что ж, давайте начнем с определения скорость изменения : Рассмотрим функцию \(f\) и предположим, что у нас есть две точки, \(x_0\) и \(x_1\). В точке \(x_0\) функция имеет вид \(f(x_0)\), а в точке \(x_1\) функция принимает значение \(f(x_1)\)
Затем изменение f определяется как \(\Delta y = f(x_1) - f(x_0)\) (которое также называют изменением y). Кроме того, изменение x определяется как \(\Delta x = x_1 - x_0)\). Проще говоря, \(\Delta x\) — это изменение x, тогда как \(\Delta y\) — это изменение значения функции из-за изменения x.
Графически:
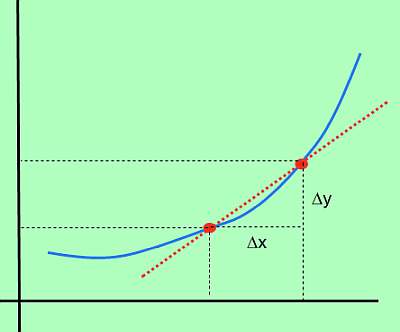
Производная формула
Таким образом, если \(\Delta x\) представляет собой изменение x, а \(\Delta y\) представляет собой изменение значения функции из-за изменения x, соответствующее скорость изменения это:
\[\text{Rate of Change} = \displaystyle \frac{\Delta y}{\Delta x} \]Итак, какова будет мгновенная скорость изменения? Это соответствует анализу того, что произойдет, если \(\Delta x\) станет действительно маленьким. Можно было бы ожидать, что \(\Delta y\) также станет маленьким, но что произойдет с курсом между \(\Delta y\) и \(\Delta x\)?
Итак, в данном контексте мгновенная скорость изменения определяется как
\[\text{Instant Rate of Change} = \displaystyle \lim_{x_1 \to x_0}\frac{\Delta y}{\Delta x} \]Итак, с точки зрения непрофессионала, мы устанавливаем \(x_0\) фиксированным и вычисляем скорость изменения для значений \(x_1\), которые все ближе и ближе к \(x_0\). Используя эту идею мгновенной скорости изменения, мы можем дать следующую формулу для производной в точке \(x_0\).
\[f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{\Delta y}{\Delta x} = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \]Если вышеуказанный предел выходит за пределы, мы говорим, что функция f дифференцируема в \(x_0\). Также будем говорить, что функция дифференцируема на множестве А, если функция дифференцируема в каждой точке множества.
Шаги для использования формулы производной
- Шаг 1: Четко определите функцию f, которую вы хотите дифференцировать
- Шаг 2: Убедитесь, что вы максимально упростили f, иначе нахождение требуемого предела может быть неоправданно усложнено
- Шаг 3: Решите, будете ли вы работать с общей точкой x0, или вы задаете конкретную числовую точку для x0
- Шаг 4: На основе определения функции используйте формулу \(f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \). То есть подставьте значения x0 и x1 в f и посмотрите, как формула выглядит алгебраически.
- Шаг 5: Упростите все, что можно, ДО того, как взять лимит
- Шаг 6: Иногда проще задать x1 = x0 + h, а затем вычислить предел, когда h сходится к 0
Обратите внимание, что шаг 6 - это шаг, который некоторым людям нравится по умолчанию. Действительно, альтернативная формула производной, которая может показаться более простой для целей упрощения, такова:
\[f'(x_0) = \displaystyle \lim_{h \to 0} \frac{f(x_0 + h) - f(x_0)}{h} \]это формула, которую вы можете найти в своем учебнике, вместо другой.
Правила производных
Вычисление производной по формуле может показаться чертовски трудоемким занятием. И действительно, это может быть трудоемким процессом, если мы решим каждый процесс дифференцирования проводить по формуле производной.
К счастью, существует ряд функций (а именно полиномы , Тригонометрические функции ), для которых мы точно знаем их производные.
Кроме того, у нас есть правила дифференциации которые позволяют нам найти производную функции, которая является Составная функция и/или комбинацию элементарных функций (для которых известна их производная), в терминах элементарных производных.
Каковы этапы вычисления производной?
- Шаг 1: Определите функцию f, которую вы хотите дифференцировать. Упростите как можно больше перед вычислением ее производной
- Шаг 2: Определите, должны ли вы использовать формулу производной или нет
- Шаг 3: Если вы должны использовать производную формулу, используйте \(f'(x_0) = \displaystyle \lim_{x_1 \to x_0}\frac{f(x_1) - f(x_0)}{x_1 - x_0} \) или вы можете использовать \(f'(x_0) = \displaystyle \lim_{h \to 0}\frac{f(x_0+h) - f(x_0)}{h} \), если это кажется более простым.
- Шаг 4: Если вам не требуется использовать формулу производной, вы можете воспользоваться основными правилами дифференцирования: Линейность, Правило Продукта , Правило Квоты и Правило Цепи , что поможет вам свести вычисление производной к использованию основных известных производных
Часто бывает так, что функция, которую вы пытаетесь найти производную for не является простой функцией, а представляет собой базовую комбинацию нескольких простых функций. Например, функция
\[f(x) = x + \cos(x) + \sin(x)\]сама по себе не является элементарной функцией, но Составная функция из трех элементарных функций: \(x\), \(\sin x\) и \(\cos x\).
Применение деривативов
Можно подумать: "Ну, производные связаны с пределами, а это супертеоретически, поэтому они не должны иметь слишком много применений", но вы будете совершенно неправы. Магия производных заключается в том, что они, по сути, представляют собой скорость изменения функций, которые могут представлять различные типы процессов.
Именно поэтому дифференциация позволяет изучить процесс изменения и сравнить изменяющиеся переменные, что имеет широкое применение.
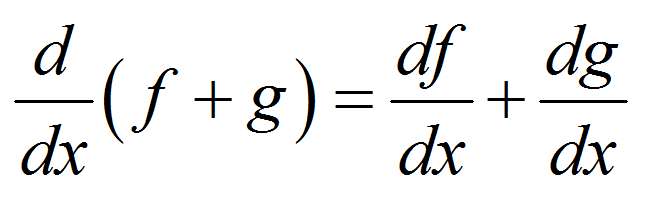
Пример: вычисление производной
Вычислите производную по x для \(f(x) = \displaystyle \frac{x}{3} + \frac{5}{4} \cos(x) - \frac{5}{4} \sin(x^2)\)
Отвечать: Предусмотрена следующая функция: \(\displaystyle f(x)=\frac{x}{3}+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right)\), для которой нам нужно вычислить ее производную.
Начальный Этап: В этом случае нам сначала нужно упростить заданную функцию \(\displaystyle f(x)=\frac{x}{3}+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right) \), и для этого мы проведем следующие шаги упрощения:
После упрощения функции мы можем перейти к вычислению производной:
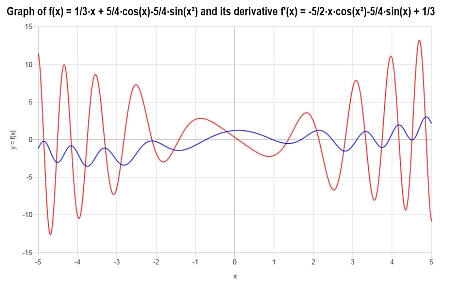
Следующий график получается для \(\displaystyle f(x)=\frac{1}{3}x+\frac{5}{4}\cos\left(x\right)-\frac{5}{4}\sin\left(x^2\right)\) на интервале \([-5, 5]\):
Пример: дифференцирование функции
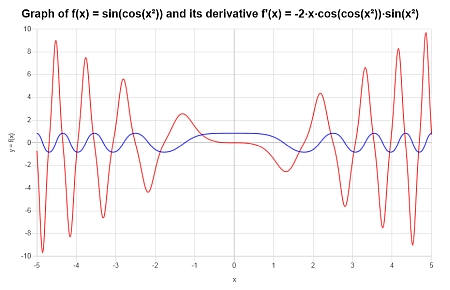
Вычислить производную от : \(f(x) = \sin(\cos(x^2))\) и представить график \(f(x)\) и \(f'(x)\).
Отвечать: Теперь у нас есть \(\displaystyle f(x)=\sin\left(\cos\left(x^2\right)\right)\).
Функция пришла уже упрощенной, поэтому мы можем перейти непосредственно к вычислению ее производной. Используя этот производный кал, мы получаем:
Таким образом, мы получаем следующий график функции на интервале \([-5, 5]\):
Пример: калькулятор производных
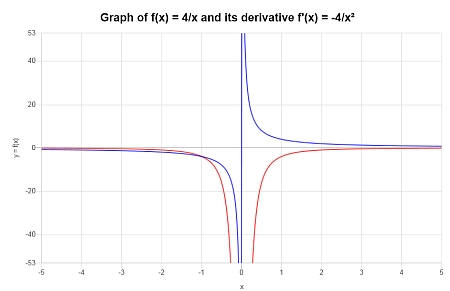
Найдите производную от \( f(x) = \displaystyle \frac{4}{x}\). Везде ли он четко определен? График это.
Отвечать: Предоставляемая функция, для которой требуется производная, — это \(\displaystyle f(x)=\frac{4}{x}\).
Дальнейшее упрощение не требуется, поэтому мы можем перейти непосредственно к вычислению его производной:
Графически:
Подробнее о производных и функциях
Этот производный калькулятор с шагами окажется для вас очень полезным, так как проведет вычисление производной любой заданной функции, показывая все этапы процесса, применяя соответствующие Правила производных , и сообщать вам, когда они применяются и почему.
Этот калькулятор также можно назвать dy dx калькулятор или калькулятор дифференциального коэффициента поскольку это именно то, что он делает, он вычисляет предел отношения dy/dx, когда dx приближается к 0.
Функции — чрезвычайно важные конструкции в математике. Наряду с дифференцированием необходимо уметь упростить функцию обычно в качестве преамбулы других, более специализированных вычислений. Существуют специальные типы функций, которые позволяют выполнять конкретные операции, например, то, что вы делаете с Полиномиальные операции .
Интересно, что многие важные элементы, такие как нахождение координат вершина параболы которые можно вывести хитрым способом, используя геометрические аргументы, можно тривиально получить с помощью дифференцирования.
Также идея о Касательная линия и Аппроксимация Первого Порядка появляются естественным образом, вытекая из понятия производного и естественного расширения.



