Подробнее о нормальном вероятностном графике

Нормальный вероятностный график — это график, который обычно используется для оценки нормальности распределения, к которому относятся переданные данные выборки.

Существуют различные типы графиков нормальности (PP, QQ и другие разновидности), но все они работают на основе одной и той же идеи. Теоретические квантили стандартного нормального распределения отображаются в виде графика против наблюдаемых квантилей.

Поэтому, если данные выборки поступают из нормально распределенная популяция , то график нормальной вероятности должен выглядеть как 45 ^О линия, со случайными вариациями вокруг нее. Если это не так, и рисунок графика нормальной вероятности значительно/систематически отклоняется от графика нормальной вероятности, то следует заподозрить, что распределение не является нормальным.

Как вычислить нормальный график вероятности?

Чтобы построить график нормальной вероятности, вам необходимо выполнить несколько конкретных шагов в определенном порядке

1. В этом конкретном случае данные упорядочены в порядке возрастания, и мы называем такие данные \(X_1, X_2, ...., X_i , ...., X_n\).
2. Для каждого \(X_i\) в этой последовательности упорядоченных данных мы вычисляем теоретические частоты \(f_i\), которые аппроксимируются с помощью следующей формулы:
\[ f_i = \frac{i - 0.375}{n + 0.25} \] (where \(i\) corresponds to the position in the ordered dataset)
3. Затем мы также вычисляем \(z_i\), соответствующую связанную z-оценку как
\[ z_i = \Phi^{-1}(f_i)\]
4. Затем график нормальной вероятности получается путем нанесения упорядоченных значений X (ваши выборочные данные) на горизонтальную ось, а соответствующих значений \(z_i\) — на вертикальную ось.

Нормальный вероятностный график excel

Вы можете построить график нормальной вероятности в Excel, но это займет некоторое время. Yo

Калькуляторы для нормального распределения и другие

Другие конструкторы диаграмм, которые вы можете использовать, это наши нормальное распределение графер , Создатель диаграмм рассеяния или наш Создатель диаграммы Парето .

Пример: расчет графика нормальной вероятности

Вопрос : Вам предоставлены следующие образцы данных: 2, 3, 4, 3, 3, 2, 3, 4, 5, 3, 2, 3, 1, 2, 3, 4, 5, 6, 3, 2, 4, 5, 6 10 10 10 12 12 1 2 3 3 и 23. Постройте нормальный вероятностный график.

Решение:

Нам нужно построить нормальный график вероятности. Вот примеры данных, которые были предоставлены:

Наблюдение:	\(X\)
1	2
2	3
3	4
4	3
5	3
6	2
7	3
8	4
9	5
10	3
11	2
12	3
13	1
14	2
15	3
16	4
17	5
18	6
19	3
20	2
21	4
22	5
23	6
24	10
25	10
26	10
27	12
28	12
29	1
30	2
31	3
32	3
33	23

Необходимо вычислить теоретические частоты \(f_i\), а также соответствующие z-оценки \(z_i\) для \(i = 1, 2, ..., 33\):

Обратите внимание, что теоретические частоты \(f_i\) аппроксимируются с помощью следующей формулы:

\[ f_i = \frac{i - 0.375}{n + 0.25} \]

где \(i\) соответствует позиции в упорядоченном наборе данных, а \(z_i\) — соответствующая связанная z-оценка. Это вычисляется как

\[ z_i = \Phi^{-1}(f_i)\]

Получается следующая таблица

Позиция (я)	X (Порядок Возр.)	ф я	з я
1	1	0.0188	-2.079
2	1	0.0489	-1.656
3	2	0.0789	-1.412
4	2	0.109	-1.232
5	2	0.1391	-1.084
6	2	0.1692	-0.957
7	2	0.1992	-0.844
8	2	0.2293	-0.741
9	3	0.2594	-0.645
10	3	0.2895	-0.555
11	3	0.3195	-0.469
12	3	0.3496	-0.386
13	3	0.3797	-0.306
14	3	0.4098	-0.228
15	3	0.4398	-0.151
16	3	0.4699	-0.075
17	3	0.5	0
18	3	0.5301	0.075
19	4	0.5602	0.151
20	4	0.5902	0.228
21	4	0.6203	0.306
22	4	0.6504	0.386
23	5	0.6805	0.469
24	5	0.7105	0.555
25	5	0.7406	0.645
26	6	0.7707	0.741
27	6	0.8008	0.844
28	10	0.8308	0.957
29	10	0.8609	1.084
30	10	0.891	1.232
31	12	0.9211	1.412
32	12	0.9511	1.656
33	23	0.9812	2.079

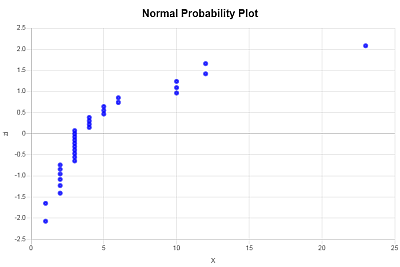
Нормальный график вероятности получается путем нанесения значений X (ваши данные выборки) на горизонтальную ось, а соответствующих значений \(z_i\) на вертикальную ось. Получается следующий график нормальности: