Калькулятор длинного деления полинома

Данный калькулятор поможет вам в процессе выполнения длинного деления между двумя заданными многочленами. Для этого вам необходимо предоставить два правильных выражения многочлена. Эти многочлены могут быть уже упрощенными или нет, и калькулятор упростит их, если это необходимо.

Когда деление многочленов вам нужно предоставить два многочлена, один из которых вы будете делить, который называется делителем, а другой - делимым.

Как только вы предоставите два действительных полиномы следующим шагом будет нажатие на кнопку "Рассчитать", которая покажет все соответствующие вычисления, необходимые для желаемого длинного деления между указанными многочленами.

Процесс проведения деления многочленов с использованием Метод Длинного Деления это относительно простой метод, но он требует очень организованного подхода, чтобы не заблудиться. Обычно лучше всего работает табличный подход, показывающий соответствующие шаги.

Более простой подход используется с Синтетическое подразделение но это применимо только в том случае, если делитель имеет степень один, поэтому имеет более ограниченный охват

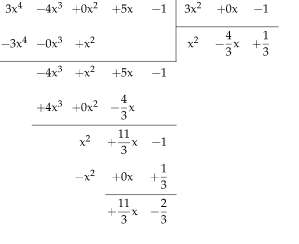
Что такое многочлен?

Многочлен - это тип простого выражения, которое объединяет с помощью сумм и вычитаний целые степени определенной переменной x (или какое бы имя переменной ни было выбрано), возможно, умноженные на константы.

Например, выражение \(p(x) = 2x^2 + x + 1\) является комбинацией выражений \(2x^2\), \(x\) и \(1\) с добавлением степени x (обратите внимание, что 1 является степенью x, как \(x^0 = 1\).

С другой стороны, \(f(x) = 2x^2 + \sin(x) + 1\) не является многочленом, так как член \(\sin(x)\) не является степенью x.

Полиномиальные операции

С многочленами, как и с числами, можно работать следующим образом сложение, вычитание, умножение и деление многочленов . Сложение и вычитание выполняются очень просто, интуитивно понятным способом. Например, если у вас есть два многочлена, \(p(x) = 2x+1\) и \(q(x) = x^3 + 2x+ 3\), сложение многочленов достигается буквальным сложением членов как

\[p(x) + q(x) = 2x + 1 + x^3 + 2x+ 3 = x^3 + 4x + 4\]

При вычитании также вычитаются соответствующие члены вычитаемого многочлена. Например, если у вас есть два многочлена \(p(x) = 2x+1\) и \(q(x) = x^3 + 2x+ 3\), то вычитание выполняется следующим образом

\[p(x) - q(x) = 2x + 1 - (x^3 + 2x+ 3) = 2x + 1 - x^3 - 2x - 3) = -x^3 -2\]

Умножение сложнее, так как необходимо перекрестное умножение терминов с использованием распределительного свойства:

\[p(x) \cdot q(x) = (2x + 1) \cdot (x^3 + 2x+ 3) = 2x \cdot x^3 + 2x \cdot 2x + 2x \cdot 3 + 1\cdot x^3 + 1\cdot1 2x+ 1\cdot 3 = 2x^4 +x^3+4x^2+8x+3\]

Деление немного сложнее, поскольку в нем задействована идея о том, что один полином не может делиться на другой именно другой многочлен. Математически, когда у нас есть два многочлена \(p(x)\) и \(s(x)\), и мы хотим разделить \(p(x)\) на \(s(x)\), мы ищем коэффициент \(q(x)\) и остаток \(r(x)\) (оба многочлена), которые обладают тем свойством, что \(p(x)= q(x)\cdot s(x) + r(x)\), с условием степень полинома \(r(x)\) меньше, чем степень \(s(x)\). Обычно это называется Разложение Евклида .

Метод длинного деления

Итак, метод длинного деления - это один из систематических способов начать с двух многочленов, которые мы хотим разделить \(p(x)\) и \(s(x)\), и найти коэффициент \(q(x)\) и остаток \(r(x)\) таким образом, чтобы

\[p(x)= q(x)\cdot s(x) + r(x)\]

Этот алгоритм чрезвычайно полезен, и хотя задача кажется простой на вид, в ней нетрудно заблудиться, если не использовать систематический подход, который гарантированно приведет к требуемому коэффициенту и остатку.

Каковы этапы выполнения длинного деления?

• Шаг 1: Определите два многочлена p(x) и s(x), которые вы хотите разделить, и определите p(x) как делитель и s(x) как делимое
• Шаг 2: Сверьте степень дивиденда p(x) со степенью s(x). Если степень s(x) больше степени p(x), то остаток равен самому дивиденду p(x), а коэффициент равен нулю: q(x) = 0, и все готово
• Шаг 3: В данном случае мы предполагаем, что степень дивиденда p(x) больше или равна степени дивиденда s(x), иначе мы бы остановились на шаге 2
• Шаг 4: Нам нужно провести итерационный процесс нахождения временного остатка, пока мы не придем к остатку, степень которого меньше степени s(x)
• Шаг 5: Временный или промежуточный остаток обновляется каждый раз, сначала находится отношение между старшим членом текущего временного остатка и делителем s(x). Затем это отношение (которое является сильным членом) умножается на s(x), и результат этого умножения вычитается из текущего временного остатка, что приводит к обновленному остатку
• Шаг 6: Этот процесс продолжается до тех пор, пока степень остатка не станет меньше степени s(x). На каждом шаге итерации степень временного остатка уменьшается по крайней мере на 1, так что процесс гарантированно завершится

В конце концов, процесс деление двух многочленов сводится к вычислению умножений - сумм многочленов, что в основном и происходит с числами. Метод длинного деления для многочленов - это распространение способа деления чисел на многочлены.

Как длинное деление связано с нахождением корней полиномиального уравнения

Предположим, что p(x) - это делитель, который вы хотите разделить, а s(x) - делимое. Согласно методу длинного деления, вы сможете найти делитель q(x) и остаток r(x) так, чтобы:

\[\displaystyle p(x) = q(x)s(x) + r(x) \]

Но иногда случается, что остаток равен r(x) = 0, и тогда мы говорим, что s(x) делит p(x) (или в точности делит p(x)). Итак, когда r(x) = 0

\[\displaystyle p(x) = q(x)s(x) \]

Это говорит о том, что для нахождения корней p(x) = 0 мы можем получить решение q(x) = 0 и s(x) = 0, по отдельности, которые являются более простыми уравнениями для решения.

Преимущества этого калькулятора для деления на длинные отрезки

Как я уже говорил, деление на длинные отрезки не слишком сложно, но требует систематического подхода. Большое преимущество использования калькулятор деления как этот, заключается в том, что вы получите все этапы процесса, показанные на рисунке

Возможно, не обязательно знать, как выполнять эти действия самостоятельно, но этот калькулятор позволяет увидеть, как это делается, с объяснением каждого шага, устраняя загадку получения остатка и коэффициента, скажем, от цифрового калькулятора, который выдаст вам ответ, не показывая шагов.

Калькулятор деления с шагами, показывающими всю работу, гарантирует, что вы получите четкое представление о том, что происходит при вычислении.

Пример: вычисление деления многочленов

Вычислите деление следующих многочленов: \(p(x) = \frac{1}{3} x^3 + \frac{5}{4}x - \frac{5}{6}\) и \(s(x) = x+3\).

Отвечать: Дан следующий многочлен: \(\displaystyle p(x) = \frac{1}{3}x^3+\frac{5}{4}x-\frac{5}{6}\), который необходимо разделить на многочлен \(\displaystyle s(x) = x+3\).

Обратите внимание, что степень дивиденда равна \(\displaystyle deg(p) = 3\), тогда как степень делителя равна \(\displaystyle deg(s)) = 1\).

Шаг 1: Ведущий член дивиденда \(\displaystyle p(x) = \frac{1}{3}x^3+\frac{5}{4}x-\frac{5}{6}\) равен \(\displaystyle \frac{1}{3}x^3\), тогда как ведущий член делителя \(\displaystyle s(x) = x+3\) равен \(\displaystyle x\).

Итак, член, который нам нужно умножить на \(x\), чтобы получить ведущий член дивиденда, это \(\displaystyle \frac{ \frac{1}{3}x^3}{ x} = \frac{1}{3}x^2\), поэтому мы прибавляем этот член к делителю. Также мы умножим его на делитель, чтобы получить \(\displaystyle \frac{1}{3}x^2 \cdot \left(x+3\right) = \frac{1}{3}x^3+x^2\), который нам нужно вычесть из дивиденда:

\[\begin{array}{rcccc} &\displaystyle \frac{1}{3}x^2 & \displaystyle & \displaystyle &\\[0.8em] \hline x+3\,) & \displaystyle \frac{1}{3}x^3 & \displaystyle & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle -\frac{1}{3}x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \end{array}\]

Шаг 2: В этом случае ведущий член текущего остатка \(\displaystyle -x^2+\frac{5}{4}x-\frac{5}{6}\) равен \(\displaystyle -1x^2\), и мы знаем, что ведущий член делителя равен \(\displaystyle x\).

Итак, член, который нам нужно умножить \(x\), чтобы получить ведущий член текущего остатка - \(\displaystyle \frac{ -1x^2}{ x} = -x\), поэтому мы прибавляем этот член к квантору. Также мы умножаем его на делитель, чтобы получить \(\displaystyle -x \cdot \left(x+3\right) = -x^2-3x\), который нам нужно вычесть из текущего остатка:

\[\begin{array}{rcccc} &\displaystyle \frac{1}{3}x^2 & \displaystyle -x & \displaystyle &\\[0.8em] \hline x+3\,) & \displaystyle \frac{1}{3}x^3 & \displaystyle & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle -\frac{1}{3}x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle +3x & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle \frac{17}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \end{array}\]

Шаг 3: В этом случае ведущий член текущего остатка \(\displaystyle \frac{17}{4}x-\frac{5}{6}\) равен \(\displaystyle \frac{17}{4}x\), и мы знаем, что ведущий член делителя равен \(\displaystyle x\).

Итак, член, который нам нужно умножить \(x\), чтобы получить ведущий член текущего остатка - \(\displaystyle \frac{ \frac{17}{4}x}{ x} = \frac{17}{4}\), поэтому мы прибавляем этот член к квантору. Также мы умножаем его на делитель, чтобы получить \(\displaystyle \frac{17}{4} \cdot \left(x+3\right) = \frac{17}{4}x+\frac{51}{4}\), который нам нужно вычесть из текущего остатка:

\[\begin{array}{rcccc} &\displaystyle \frac{1}{3}x^2 & \displaystyle -x & \displaystyle +\frac{17}{4}&\\[0.8em] \hline x+3\,) & \displaystyle \frac{1}{3}x^3 & \displaystyle & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle -\frac{1}{3}x^3 & \displaystyle -x^2 & \displaystyle & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle -x^2 & \displaystyle +\frac{5}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle & \displaystyle x^2 & \displaystyle +3x & \displaystyle \\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle \frac{17}{4}x & \displaystyle -\frac{5}{6}\\[0.8em] \displaystyle &\displaystyle & \displaystyle & \displaystyle -\frac{17}{4}x & \displaystyle -\frac{51}{4}\\[0.8em] \hline \displaystyle &\displaystyle & \displaystyle & \displaystyle & \displaystyle -\frac{163}{12}\\[0.8em] \end{array}\]

который завершает это вычисление, так как степень текущего остатка \(r(x) = -\frac{163}{12}\) меньше степени делителя \(s(x) = x+3\).

Заключение: Therefore, we conclude that for the given dividend \(\displaystyle p(x) = \frac{1}{3}x^3+\frac{5}{4}x-\frac{5}{6}\) and divisor \(\displaystyle s(x) = x+3\), we get that the quotient is \(\displaystyle q(x) = \frac{1}{3}x^2-x+\frac{17}{4}\) and the remainder is \(\displaystyle r(x) = -\frac{163}{12}\), and that