Концепция функции чрезвычайно важна, и она абсолютно вездесуща в математике. Вот почему нам нужно хорошенько освежить его, прежде чем пытаться понять некоторые полезности, которые появятся позже, когда мы углубимся в темы математического анализа, такие как дифференциация и интеграция.

ЧТО ТАКОЕ НАБОР?

Первый элемент, который нам нужно понять, - это концепция установленный . Набор - это просто набор элементов. Итак, набор довольно просто определяется путем знания, какие элементы принадлежат набору, а какие нет. Это кажется сверхпростой задачей, и теория множества должна быть просто сведена к наличию однозначных правил для определения того, какие элементы принадлежат множеству.

Например, давайте определим набор четных чисел и назовем его \(E\). Почему это вообще набор? Потому что у него есть однозначное правило для определения того, какие элементы принадлежат \(E\): действительное число \(x\) принадлежит \(E\), если оно делится на 2. Правило однозначно работает для каждого действительного числа, определяющего, принадлежит ли оно \(E\). Почему я говорю "однозначно" и повторяю. Потому что это важно. Однозначно означает, что невозможно сделать вывод, что заданные \(x\) принадлежат и не принадлежат \(E\). К сожалению, иногда вещи выходят за рамки нашего воображения. Вопреки нашей интуиции, множество, определяемое простым правилом принадлежности, может привести к неоднозначной (противоречивой) классификации принадлежности, как показал Бертран Рассел в своем знаменитом парадоксе. Рассел показал, что следует использовать более тщательное определение того, что такое набор.

Для всех практических целей мы будем думать о множестве как о совокупности элементов, определяемых правилом принадлежности. .

ЧТО ПРЕДСТАВЛЯЕТСЯ ИЗ ДВУХ НАБОРОВ?

Пусть \(A\) и \(B\) будут установлены в контексте определения, данного выше. Продукт \(A\times B\) из двух наборов является другим набором, который определяется как набор всех возможных упорядоченных пар формы \(\left( a, b \right)\), где \(a\) принадлежит \(A\), а \(b\) принадлежит \(B\). Итак, \(A\times B\) - это набор, а его элементы - это упорядоченные пары формы \(\left( a ,b \right)\). Не позволяйте этим обозначениям произвести на вас впечатление. Когда я говорю "упорядоченные пары формы \(\left( a, b \right)\)", символ \(\left( a, b \right)\) является составленным символом, чтобы указать элемент, состоящий из двух сущностей \(a\) и \(b\), и идентифицировать первый элемент как \(a\), а второй элемент как \(b\) . Вот и все. Вместо \(\left( a,b \right)\) мы могли бы выбрать символ \(a\_b\), и это сработало бы нормально.

Вы должны меня простить, но я должен написать математическое определение произведения двух множеств (мы тоже можем умножать множества… как вы думаете, мы бы остановились только на числах, а?):

\(A\times B=\left\{ \left( a,b \right):\,\,\,a\in A,\,\,\,b\in B \right\}\)

Причина, по которой я пишу определение, состоит в том, чтобы вы взглянули на него и осознали, как, используя очень компактную нотацию, мы говорим точно так же, как я определил это словами в предыдущем абзаце. Я надеюсь, что вы развеете страх перед чтением математических утверждений. Иногда математики могут быть фанками, но они находят хорошие, недвусмысленные и компактные обозначения. И, следовательно, математический язык СУПЕР легко читается. Верно? Верно? Пожалуйста, скажите мне, что я прав ...

Примечание: по историческим причинам произведение двух наборов \(A\times B\) обычно называется Декартово произведение .

ТЕПЕРЬ ОПРЕДЕЛЕНИЕ ФУНКЦИИ (НАКОНЕЦ)

Хорошо, я соврал, есть еще один шаг перед определением функции. Нам необходимо определить понятие связь . Что такое отношение? Помимо своего обычного использования в качестве английского слова, отношение - это просто подмножество декартова произведения. ЛЮБОЕ подмножество декартова произведения - это отношение. Итак, если \(A\) и \(B\) установлены, набор \(R\) является отношением, если \(R\subseteq A\times B\). Поскольку любой набор можно рассматривать как подмножество самого себя, тогда все декартовы произведения сами являются отношениями.

Наденьте на рамку:

Отношение - это набор, который является подмножеством декартова произведения.

Давайте сделаем более наглядным. Рассмотрим набор \(A=\left[ 0,1 \right]\) (который представляет собой все действительные числа, которые больше или равны 0, и они также меньше или равны 1). Что такое декартово произведение \(A\times A\)? Давайте попугаем то, что мы только что узнали. Декартово произведение \(A\times A\) равно \(\left[ 0,1 \right]\times \left[ 0,1 \right]\), в данном случае это набор всех пар \(\left( x, y \right)\), где как \(x\), так и \(y\) принадлежат \(\left[ 0,1 \right]\). Декартовы произведения обычно легко построить на графике. Посмотрите на заштрихованную область ниже:

Итак, что могло бы создать отношение? Мы можем "вырезать" все, что захотим, из затененной области выше, и то, что осталось, - это отношение в \(\left[ 0,1 \right]\times \left[ 0,1 \right]\). Например, мы можем вырезать "углы", чтобы получить следующую подобласть:

Вышеуказанный регион (набор) является отношением. Почему? Потому что это подмножество декартова произведения \(\left[ 0,1 \right]\times \left[ 0,1 \right]\). Но мы можем выкроить еще больше. Как насчет того, чтобы вырезать четверть круга? См. Регион ниже.

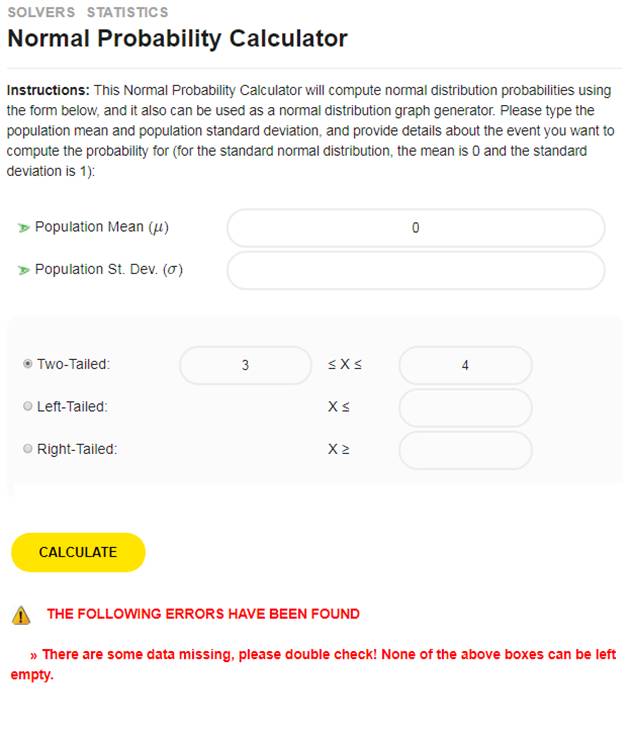
Вышеуказанный регион (набор) является отношением. Почему? Опять же, потому что это подмножество декартова произведения \(\left[ 0,1 \right]\times \left[ 0,1 \right]\).

Теперь позвольте мне привести пример двух отношений в \(\left[ -1,1 \right]\times \left[ -1,1 \right]\). См. Графики ниже:

Отношение 1

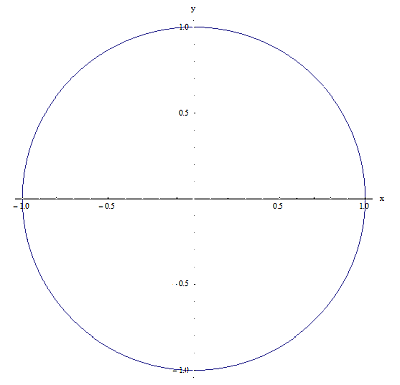
Отношение 2

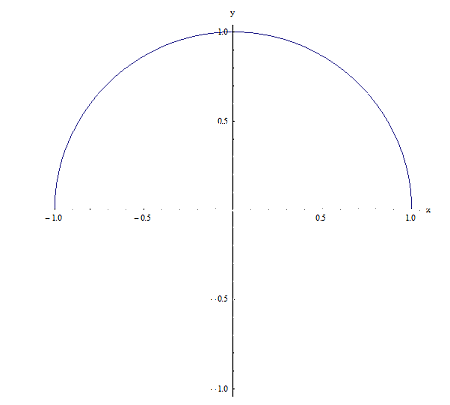
Очевидно, что они оба являются связями (поскольку они оба содержатся в декартовом произведении \(\left[ -1,1 \right]\times \left[ -1,1 \right]\), но у них есть одно ключевое отличие: для отношения 1 для данной точки x на \(\left[ -1,1 \right]\) есть две точки \({{y}_{1}}\) и \({{y}_{2}}\), которые имеют свойство \(\left( x,{{y}_{1}} \right)\) и __XYZ_F к отношению 1. Например, для x = 0 есть две точки \({{y}_{1}}=1\) и \({{y}_{2}}=-1\), такие что \(\left( 0,1 \right)\) и\(\left( 0,-1 \right)\) принадлежат отношению 1. Теперь для отношения 2 это не так, потому что, например, для x = 0 это только \(y=1\), делает точку \(\left( 0,1 \right)\) принадлежащей отношению 1.

Наконец, мы можем определить функцию: функция \(R\) - это набор, который является отношением, и у него также есть свойство, что если точка \(\left( x,y \right)\) принадлежит к \(R\), то нет другой точки \(\bar{y}\), отличной от \(y\), которая имеет свойство \(\left( x,\bar{y} \right)\)_A___A__ также. Другими словами, функция - это отношение с дополнительным требованием, чтобы каждый \(x\) в своем домене был связан только с одним \(y\).

Как узнать, как отличить функцию от отношения ??

Гаджеты! Мы используем небольшой трюк, называемый "тест вертикальной линии": мы рисуем воображаемую вертикальную линию и обводим ее, перемещая ее слева направо до упора, и составляем мысленную карту того, где вертикальная линия пересекает отношение.

• Если в ЛЮБОЙ точке вертикальная линия пересекает отношение БОЛЕЕ чем в одной точке, то отношение не проходит проверку вертикальной линии, и тогда отношение не является функцией.

• Если в ЛЮБОЙ точке вертикальная линия не пересекает отношение более чем в одной точке, то отношение проходит проверку вертикальной линии, и тогда отношение является функцией.

См. Два примера ниже:

Пример 1: Тест вертикальной линии не проходит, потому что вертикальная линия, показанная на рисунке, пересекает отношение более чем в одной точке: НЕ ФУНКЦИЯ

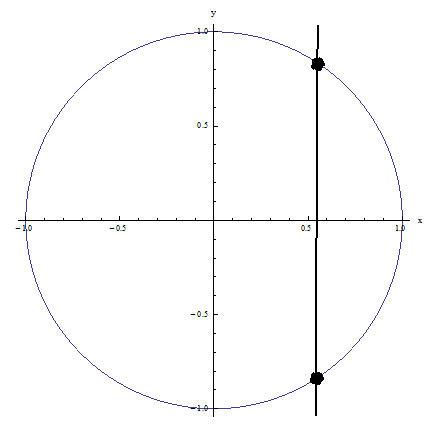
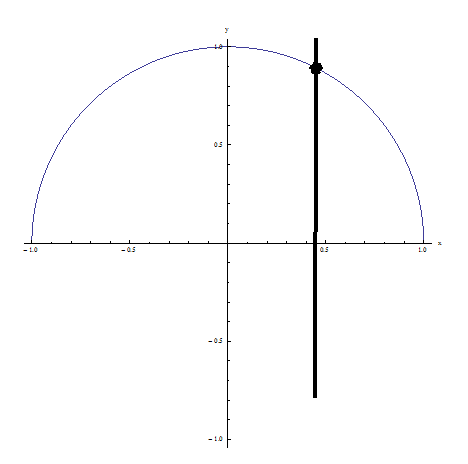
Пример 2: Он проходит проверку вертикальной линии, потому что ни одна вертикальная линия не пересекает отношение более чем в одной точке: ЭТО ФУНКЦИЯ!

Существует множество графических приложений, в которых можно выполнять функции, включая расчет горизонтальные асимптоты , вертикальные асимптоты и наклонные асимптоты, если применимо.