Полиномиальный график

Используйте этот калькулятор, если вам нужна помощь в построении графика полиномиальной функции. Процесс прост: вам нужно просто ввести полиномиальную функцию, график которой вы хотите построить. Вы можете написать что-то вроде "3x^3 + x - 1", а можете предварить это именем функции, например, "p(x) = 3x^3 + x - 1".

Коэффициенты предоставленного полинома не обязательно должны быть целыми, они могут быть дробями или любым допустимым алгебраическим выражением. Предоставленный вами многочлен может быть упрощенным или нет, это не имеет значения.

После того, как полином будет задан, вы можете по желанию определить диапазоны значений x, которые будут отображаться на графике, а затем нажать кнопку "Рассчитать", и вскоре будут показаны все этапы процесса.

полиномиальные функции являются одними из самых важных объектов, которые вы найдете как в алгебре, так и в исчислении. Кроме того, полиномы приводят к необходимости решать полиномиальные уравнения, которые имеют множество применений везде, во всех сферах жизни, даже за пределами математики.

Основы полиномиальных функций

Напомним, что полиномиальная функция имеет следующий вид:

\[\displaystyle p(x) = a_0 + a_1 x + a_2 x^2 + .... + a_n x^n \]

где мы предполагаем, что \(a_n \ne 0\), и говорим, что степень полинома в данном случае равна \(n\), а ведущий коэффициент - \(a_n\). Непрофессиональный способ определения степени многочлена заключается в том, что она соответствует наибольшей мощности, присутствующей в выражении многочлена.

Например, \(p(x) = 3x^2 + 2x - 1\) является многочленом степени 2, и его ведущий коэффициент равен 3. Теперь, например, \(p(x) = \sin(3x^2 + 2x - 1)\) НЕ является многочленом.

Как сделать графики многочленов?

Построение графика многочленов в принципе показывает то же самое, что и построение графика любой другой функции. Если бы вы делали это вручную, вы бы занесли в таблицу несколько значений x и y, и провели бы кривую, которая более или менее проходит через точки, которые вы получаете в своей таблице.

Естественно, этот метод немного примитивен, поскольку в общем случае мы не можем знать обязательно полный график функции, зная лишь кучу точек, которые мы табулируем.

К счастью, для многочленов задача немного проще, и в действительности мы можем многое узнать о его графике, зная его ведущий коэффициент и степень.

Этапы построения графиков полиномиальных функций

Граф многочлена в конечном счете зависит от конкретного коэффициента каждого многочлена. Но мы можем сделать несколько сильных утверждений о конечном поведении многочленов и существовании действительных корней.

Напомним, что конечное поведение полинома - это поведение полинома, когда x очень большой и отрицательный, и когда x очень большой и положительный.

• Шаг 1: Определите полиномиальную функцию и упростите ее, если сможете, так как упрощенные выражения легче изображать на графике
• Шаг 2: Знаете ли вы корни многочлена? Если это действительные корни, то вы знаете точки пересечения многочлена с осью x, что дает вам сильную графическую ссылку
• Шаг 3: Если степень полинома нечетная, то конечное поведение будет противоположным для больших отрицательных значений x и больших положительных значений x. Если ведущий коэффициент положительный, то при больших отрицательных значениях x полином будет очень большим и отрицательным, а при больших положительных значениях x полином будет очень большим и положительным. Если ведущий коэффициент отрицательный, то для больших отрицательных значений x полином будет очень большим и положительным, а для больших положительных значений x полином будет очень большим и отрицательным
• Шаг 4: Если степень полинома четная, то конечное поведение будет одинаковым для больших отрицательных значений x и больших положительных значений x. Если ведущий коэффициент положительный, то для больших отрицательных и положительных значений x полином будет очень большим и положительным. Если ведущий коэффициент отрицательный, то для больших отрицательных и положительных значений x полином будет очень большим и отрицательным
• Шаг 5: Если степень многочлена нечетная, то многочлен хотя бы раз пересечет ось x (значит, у него есть хотя бы один вещественный корень), тогда как при четной степени многочлен не обязательно пересечет ось x
• Шаг 6: Многочлен степени n пересекает ось x не более n раз. Например, многочлен степени 4 может пересечь ось х не более 4 раз

Так, например, кубический многочлен может пересечь ось x не более 3 раз, но это не обязательно.

Графический калькулятор

Каковы преимущества использования графического калькулятора? Многие. Но это не значит, что умение точно начертить многочлен с помощью ручки и бумаги не является хорошим навыком.

\[\displaystyle \frac{a}{b} \times \frac{c}{d} = \displaystyle \frac{ac}{bd} \]

• Преимущество 1: Вы убедитесь, что получили точное изображение реального графика многочлена
• Преимущество 2: Вы можете использовать его для проверки собственной работы, чтобы убедиться, что вы следовали правильным шагам
• Преимущество 3: Хороший калькулятор выбирает соответствующее окно для отображения наиболее важных аспектов графика

Хороший график может многое рассказать о свойствах функции, то же самое относится и к многочленам. Построение графика многочлена может помочь вам наглядно представить, какой тип корней имеет многочлен.

Советы и рекомендации

Будьте осторожны с чрезмерным прочтением того, что вы видите на графике полинома. Вы не можете с легкостью определить корни с кратностью, поэтому ничто не заменяет действительную функцию.

Если вы хотите попробовать другие типы функций, попробуйте следующее график функции инструмент.

Пример: построение графиков полиномиальных функций

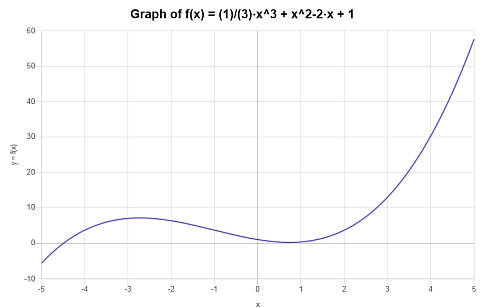
Постройте график следующего многочлена: \(p(x) = \frac{1}{3} x^3 + x^2- 2x +1 \)

Отвечать: Нам дано следующее полиномиальное выражение, которое необходимо вычислить: \(\displaystyle \frac{1}{3} x^3 + x^2- 2x +1\).

Представленное выражение является невыводимым, поэтому упрощать нечего.

Для заданного полиномиального выражения на интервале \([-5, 5]\) получен следующий график:

Пример: график полинома

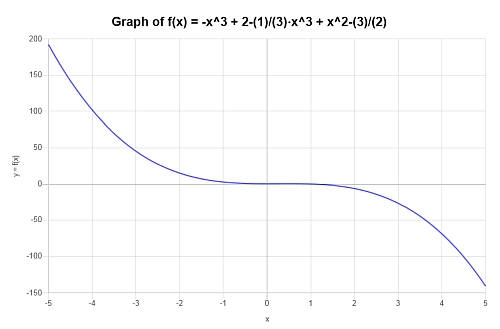
Упростите и постройте график: \(p(x) = x^4 - x^3 + 2 - \frac{1}{3}x^3 + x^2 - \frac{3}{2}\)

Отвечать: Теперь нам нужно работать с: \(\displaystyle -x^3+2-\frac{1}{3}x^3+x^2-\frac{3}{2}\).

Получается следующее упрощение:

что завершает процесс упрощения полинома.

Таким образом, получается следующий график для \(\displaystyle -\frac{4}{3}x^3+x^2+\frac{1}{2}\) на интервале \([-5, 5]\):

Пример: больше полиномиальных графов

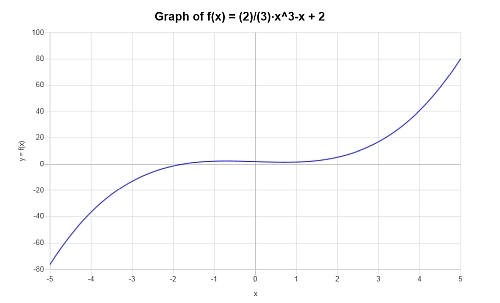
Найдите график следующего многочлена \( p(x) = \frac{2}{3} x^3 - x +2 \).

Отвечать: Для данного примера предоставленный многочлен имеет вид: \(\displaystyle \frac{2}{3} x^3 - x +2 \).

В этом случае полученное выражение является несводимым, поэтому упрощать нечего.

Для заданного полиномиального выражения на интервале \([-5, 5]\) получен следующий график:

Больше калькуляторов полиномов

Построение графиков многочленов чрезвычайно полезно, поскольку показывает нам основные характеристики их поведения в окрестности корней и их конечное поведение. Построение графиков обычно сопровождается определением того, где приблизительно могут находиться корни, что может быть полезно при использовании факторизация многочленов также.

Хотя мы можем многое узнать о многочлене, просто построив его график, нам все равно необходимо пройти через процесс попытки определить находить рациональные корни в качестве отправной точки для решение полиномиальных уравнений со степенью выше 2 (это, которые не являются квадратные уравнения ).

Систематическое угадывание или нахождение рациональных корней, в паре с использованием Длинный дивизион или же Синтетическое подразделение поэтому для использования теорема факторов может привести к успешному поиску полиномиальные корни но такой подход не всегда работает, и часто приходится полагаться на калькулятор для нахождения численных приближений.