Полиномиальные функции

Этот калькулятор полиномиальных функций поможет вам вычислить функции полиномов, вычисляя и упрощая любое полиномиальное выражение, которое вы предоставите.

Вы можете предоставить любое выражение с полиномами, и будет проведено вычисление и необходимые шаги по упрощению, чтобы оставить полиномиальную функцию в ее наиболее компактной форме. Затем будет предоставлен график полинома

Затем, как только будет задано правильное полиномиальное выражение, можно нажать на кнопку ниже, кнопку "Рассчитать", и все необходимые шаги процесса будут показаны.

Алгебра дробей включает в себя преобразование дробей, такое как использование общего знаменателя, и использование основных арифметических правил. В целом, процесс вычисления может быть трудоемким, хотя его можно выполнять систематически, без особых проблем.

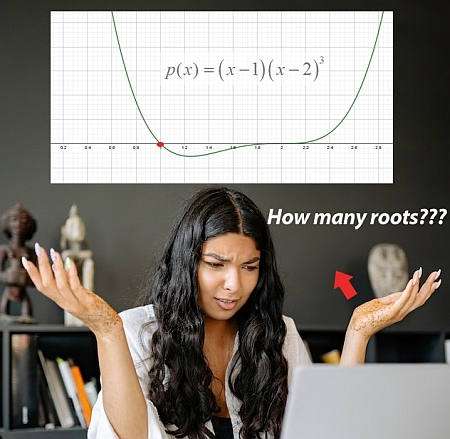
Что такое полиномиальная функция?

Полиномы, в самом простом объяснении, - это функции, которые состоят только из мощностей \(x\), возможно, умноженных на числовые константы, которые складываются (или вычитаются) вместе. Например, \(p(x) = x^3 + 2x^2 + 1\) является полиномиальной функцией, поскольку она состоит из умноженных на константы степеней \(x\), сложенных вместе. В этом случае \(1 = x^0\), так что константа также является мощностью \(x\). ..:

В общем случае полиномиальная функция имеет следующий вид:

\[\displaystyle p(x) = a_0 + a_1 x + a_2 x^2 + .... + a_n x^n \]

с \(a_n \ne 0\). В этом случае мы говорим, что степень полинома (или его порядок) равен \(n\), что является наибольшей мощностью, присутствующей в полиномиальной функции.

Кроме того, коэффициент \(a_n\) называется ведущий коэффициент , а \(a_n x^n\) называется ведущий термин . Ведущий коэффициент и степень полинома определяют его конечное поведение (то есть поведение, когда абсолютное значение x велико).

Каковы этапы работы с полиномиальной функцией?

• Шаг 1: Четко определите выражение, с которым вы хотите работать, расширяйте и упрощайте его
• Шаг 2: Проверьте, соответствуют ли члены, в которых участвует переменная x, только степеням x, иначе вы останавливаетесь, это не многочлен
• Шаг 3: Убедитесь, что все степени x умножаются на константу (которая может быть '1'), и эти члены появляются как слагаемые или вычитаемые в выражении

Важно убедиться, что у вас есть полиномиальная функция, чтобы вы могли применить результаты, которые относятся исключительно к полиномам, например, а теорема факторов , теорема об остатке и Теорема о рациональном нуле которые чрезвычайно полезны для поиска решений полиномиальных уравнений, широко используемых в различных приложениях.

Кроме того, преимущество работы с полиномиальными функциями заключается в том, что вы можете легко проводить деление многочленов либо с помощью Длинный дивизион , или же Синтетическое подразделение в случае, если делитель является линейным.

Существуют ли важные полиномиальные функции?

Действительно. Существуют пресловутые многочлены степени 2, которые мы называем квадратичные многочлены которые широко изучаются в курсе алгебры. Причина этого в том, что их можно полностью проанализировать с помощью точных формул. Например, у вас есть формула для вершины , и знаменитая квадратичная формула используется для нахождения корней для квадратичные многочлены :

\[\displaystyle x = \displaystyle \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]

Существуют также многочлены степени 2, которые мы называем кубические многочлены которые также имеют явные формулы, но которые обычно считаются более сложными и обычно не изучаются в базовых курсах алгебры.

Что я знаю о конечном поведении многочлена?

Конечное поведение полинома в конечном итоге зависит от самого полинома, но несколько вещей можно сказать, основываясь на его степени

• Факт 1: Для квадратичных многочленов график раскрывается вверх (если ведущий коэффициент положителен) или вниз (если ведущий коэффициент отрицателен), и функция сходится к бесконечности или минус бесконечности (в зависимости от знака ведущего коэффициента) с обеих сторон
• Факт 2: Для многочленов со степенью, которая является нечетной (например, со степенью 3), будет хотя бы один вещественный корень, и функция сходится к бесконечности с одной стороны и к минус бесконечности с другой стороны
• Факт 3: Для многочленов с четной степенью (например, со степенью 4) не обязательно будут существовать вещественные корни (точка, которую график пересекает по оси x), а функция сходится к бесконечности или минус бесконечности (в зависимости от знака ведущего коэффициента) с обеих сторон

Итак, полиномы работают в больших пределах при больших значениях x, а будут ли их значения положительными или отрицательными при положительных значениях x (в их конечном поведении), зависит от знака ведущего коэффициента.

Советы: в чем преимущества использования калькулятора полиномиальных функций

Калькуляторы полиномов могут гарантировать, что вы придете к правильному ответу. Действительно, вычисления полиномов не являются сложными, но они могут быть громоздкими, и в них нетрудно допустить ошибки.

Избегайте алгебраических ошибок, проверяя свою работу с помощью этого калькулятора, чтобы убедиться в согласованности окончательного ответа и шагов, использованных для его получения.

Пример: полиномиальная функция

Вычислите следующую полиномиальную функцию \((x-3)(x-1)(x-4)\)

Отвечать: Нам дано следующее полиномиальное выражение, которое необходимо вычислить: \(\displaystyle (x-3)(x-1)(x-4)\).

Получается следующий расчет:

что завершает процесс упрощения полинома.

Следующий график получен для \(\displaystyle x^3-8x^2+19x-12\) на интервале \([-5, 5]\):

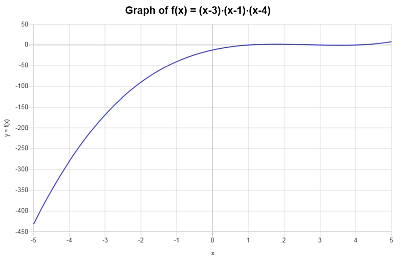
Пример: вычисление полиномиальной функции

Является ли это полиномиальной функцией: \(\frac{1}{3} x^3+ \frac{5}{4}(x-3)(x - \frac{5}{6})\)

Решение:

Нам дано следующее полиномиальное выражение, которое необходимо вычислить: \(\displaystyle \frac{1}{3} x^3+ \frac{5}{4}(x-3)(x - \frac{5}{6})\).

Получается следующий расчет:

что завершает процесс упрощения.

Графически для упрощенной функции \(\displaystyle \frac{1}{3}x^3+\frac{5}{4}x^2-\frac{115}{24}x+\frac{25}{8}\) на интервале \([-5, 5]\) получено следующее:

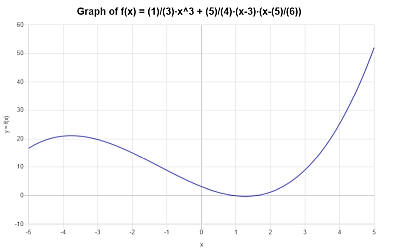
Пример: использование полиномиального калькулятора

Рассчитайте \( x^2 - (2x - 1)x \).

Отвечать: В этом последнем примере у нас есть \(\displaystyle x^2 - (2x - 1)x \), который нам нужно упростить.

Получается следующий расчет:

что завершает упрощение.

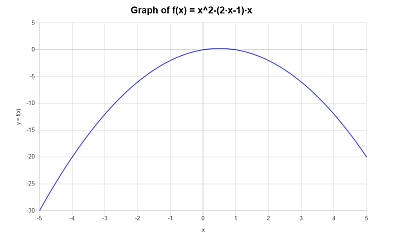
Следующий график получен для \(\displaystyle -x^2+x\) на интервале \([-5, 5]\):

Больше калькуляторов по алгебре

Полиномиальные функции являются буквально центральной частью алгебры. Для базовых приложений, квадратичные многочлены будут играть ключевую роль и экономика, физика и инженерия.

Полиномиальные функции обладают чрезвычайно мощными свойствами, особенно при вычислении полиномиальные корни , которые имеют большое значение в приложениях.