Problema: A seguinte saída foi estabelecida, que retoma os resultados de uma logística regressão realizada em emparelhadas de empresas cotadas publicamente no Reino Unido com e sem falência. As variáveis ​​independentes empregadas são as seguintes:

PBTCL_1 é o lucro antes dos impostos dividido pelo passivo circulante.

CLTA_1 é o passivo circulante para o ativo total.

NCI_1 é o intervalo sem crédito, que é uma medida de quanto tempo (em dias) uma empresa pode continuar a negociar sem geração de receita.

CATL_1 é o ativo circulante para o passivo total.

Todos esses são calculados usando dados retirados das últimas contas publicadas antes da falha.

A variável dependente é dicotômica com empresas falidas sendo atribuídas a 1 e empresas não falidas 0.

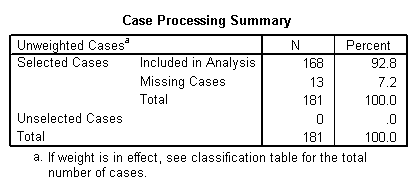
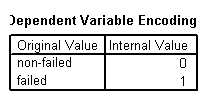
Bloco 0: Bloco inicial

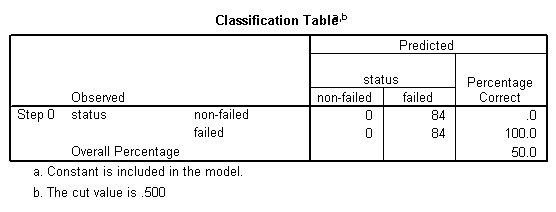
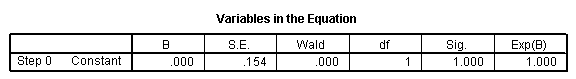
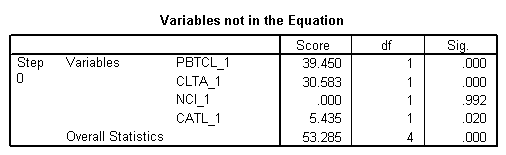
Bloco 1: Método = Enter

Você deve realizar uma avaliação financeira e estatísticas dessas informações.

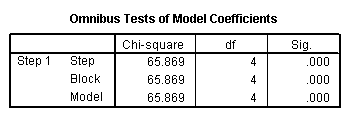
Solução: Observe que o modelo logístico é significativo no geral, p = 0,000. Além disso, foi descoberto que Nagelkerke R Square = 0,432, o que indica uma qualidade de ajuste relativamente aceitável para este modelo.

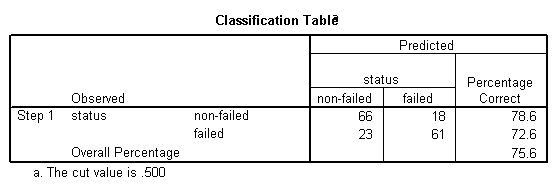
Observa-se que entre as empresas não falidas, 78,6% delas foram classificadas corretamente, enquanto entre as empresas falidas 72,6% delas foram classificadas corretamente, o que representa um total de 75,6% das empresas classificadas corretamente no geral, o que indica uma taxa de classificação relativamente boa.

O modelo logístico é

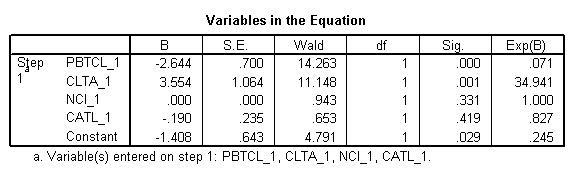
\[\ln \left( \frac{{\hat{p}}}{1-\hat{p}} \right)=-1.408-2.644*PBTCL\_1+3.554*CLTA\_1+0.000*NCI\_1-0.190*CATL\_1\]

onde \(\hat{p}\) corresponde à probabilidade de uma empresa falhe. Do ponto de vista financeiro, seguimos as seguintes condições:

· Para um aumento de 1 ponto no lucro antes de impostos dividido pelo passivo circulante, a chance de insolvência diminui em 92,9%. Esta mudança é significativa, p = 0,000 <0,05

· Para um aumento de 1 ponto no passivo circulante em relação ao ativo total, a chance de insolvência aumenta em 3.294,10%. Essa mudança é significativa, p = 0,001 <0,05

· Para um aumento de um dia no intervalo sem crédito, as chances de falha não mudam. Este coeficiente não é significativo, p = 0,331> 0,05

· Para um aumento de 1 ponto no ativo circulante em relação ao passivo total, a chance de insolvência diminui em 17,3% (essa redução é significativa, p = 0,029 <0,05)