Qual è la radice quadrata di 64?
A volte una semplice domanda come quella che è la radice quadrata di 64 ha una risposta che può confonderne alcuni.In questo caso, dissiberemo un paio di miti.
L'obiettivo principale in questo tutorial è quello di imparare alcune cose sulle radici e sui radicali quadrati, in modo che tu sia in grado di rispondere alle domande su di esso senza esitazione.
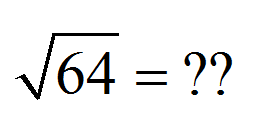
La prima cosa è prima.Scandiamo la definizione della radice quadrata:
La radice quadrata di un dato numero è il positive Numero (o zero) in modo che quando quadrati si traducono in quel dato numero .
Questo è tutto.Quindi, dato un numero \(x\), la sua radice quadrata è un numero \(b\) in modo che \(b \ge 0\) e
\[b^2 = x\]Guardando l'espressione di cui sopra, possiamo vedere che se \(b\) sarà la radice quadrata di \(x\), quindi \(x = b^2\), e poiché un numero quadrato non può essere negativo, \(x\) può essere solo non negativo (se vogliamo essere in grado di essere in grado diTrova la sua radice quadrata).
Conclusione : Possiamo solo calcolare radici quadrate di valori non negativi \(x\).O disse diversamente, il Dominio della Funzione. \(\sqrt x\) è \([0,+\infty)\).
Quindi, rispondendo alla nostra domanda iniziale:
Qual è la radice quadrata di 64?
Sulla base di ciò che abbiamo definito, dobbiamo trovare un valore non negativo \(b\) in modo che \(b^2 = 64\).Qualsiasi numero che soddisfa queste proprietà viene in mente?
Bene, sì, cosa succede se ci avessimo provato con \(b = 8\)?OK, quindi \(b = 8\) non è negativo, e \(b^2 = 8^2 = 64\).
Quindi, abbiamo trovato la radice quadrata di 64, che è 8, perché 8 non è negativa, e \(8^2 = 64\).Scriviamo questo come:
\[ \sqrt{64} = 8 \]Il mito sulla funzione radice quadrata
Ora andiamo all'argomento che ha motivato questo tutorial ... La definizione sopra indicata della radice quadrata ci consente di scartare la dichiarazione comune che "la radice quadrata di 64 è più o meno 8", che è sbagliato.Infatti
\[\sqrt{64} =\not \pm 8\]Ora, possiamo capire perché tale mito continua.Infatti, entrambi 8 e -8 hanno la proprietà che \(8^2 = 64\) e \((-8)^2 = 64\).Quindi, perché -8 non è la radice quadrata di 64?
Poiché per definizione, abbiamo detto che la radice quadrata deve essere quel numero non negativo che ha la proprietà che al quadrato equivale al numero dato.E -8 fallisce la condizione di essere non negativo.
Il grafico della funzione radice quadrata
Guarda il grafico della funzione radice quadrata qui sotto:
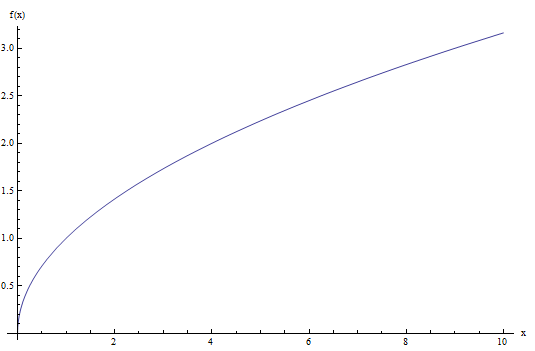
Come puoi vedere, quella funzione richiede solo valori non negativi e trasmette in realtà il test della linea verticale, quindi è una funzione.
Quindi alla fine, la definizione della radice quadrata come il non negativo \(b\) in modo che \(b^2 = x\) rende la radice quadrata una funzione.
Se infatti abbiamo avuto quel \(\sqrt{64} = \pm 8\), allora \(\sqrt x\) non sarebbe una funzione, sarebbe invece una relazione, perché la linea verticale a \(x = 64\) attraverserebbe il grafico due volte (a 8 e -8).
Che dire di altre funzioni radicali?
Esistono altri tipi di funzioni radicali.Ad esempio, la radice cubica \(\sqrt[3] x\).In questo caso, non è necessario effettuare una regola per quale radicale scegliere, perché la radice cubica di un dato numero \(x\) è il numero \(b\) in modo che \(b^3 = x\).
Radice cubica
Per il caso di radice cubica, non è necessario effettuare distinzioni perché per un dato \(x\) ci sarà solo un numero \(b\) tale che \(b^3 = x\).
Per esempio
\[\sqrt[3]{64} = 4\]Semplicemente perché \(4^3 = 64\).o
\[\sqrt[3]{-64} = -4\]Semplicemente perché \((-4)^3 = -64\).Questo è, non c'è ambiguità come nel caso della radice quadrata.
Radice quartica
Per il caso di radice quartico, è simile alla radice quadrata.Avremo quel \(\sqrt[4] x = b\) se \(b \ge 0\) e \(b^4 = x\).
Per esempio
\[\sqrt[4]{16} = 2\]Perché \(2^4 = 16\) e \(2 \ge 0\).Ma
\[\sqrt[4]{16} =\not -2\]Perché sebbene \((-2)^4 = -16\), abbiamo che \(-2 < 0\) quindi la condizione non negatività non è soddisfatta.
Che ne dici di N-th root \(\sqrt[n] x\) in generale ???.
Sono sicuro che tu abbia indovinato.
Per \(n\) Anche, la situazione è come la radice quadrata: \(\sqrt[n] x = b\) se \(b \ge 0\) e \(b^n = x\).
Per \(n\) dispari, la situazione è come la radice quadrata: \(\sqrt[n] x = b\) se \(b^n = x\).
Maggiori informazioni sul calcolo della radice quadrata
Una cosa su cui abbiamo fatto l'accento era che la funzione radice quadrata \(\sqrt x\) ha bisogno di prendere un argomento non negativo \(x\) se volevamo essere in grado di calcolare la radice quadrata.
Abbiamo tradito un po ', perché non abbiamo scritto la frase completa: la funzione radice quadrata \(\sqrt x\) ha bisogno di prendere un argomento non negativo \(x\) se volevamo essere in grado di calcolare la radice quadrata nella linea reale.
Ma, se \(x < 0\), questo è, se \(x\) è negativo, allora \(\sqrt x\) è ancora definito, ma non come un numero reale ma come numero complesso.
L'unità base della radice quadrata complessa è la radice quadrata di -1.Cos'è \(\sqrt{-1}\) ???
Inserisci i numeri complessi: c'è un numero complesso, chiamato \(i\) così
\[\sqrt{-1} = i \]Da quel momento in poi, le proprietà della radice quadrata funzionano tutte le stesse.Per esempio:
\[\sqrt{-4} = \sqrt{4} \sqrt{-1} = 2\sqrt{-1} = 2i \]