Calcolatore della formula del punto medio

Questa calcolatrice ti permetterà di trovare il punto medio tra due punti. Tutto quello che devi fare è fornire le coordinate dei due punti, quindi fare clic su "Calcola" per visualizzare tutti i passaggi.

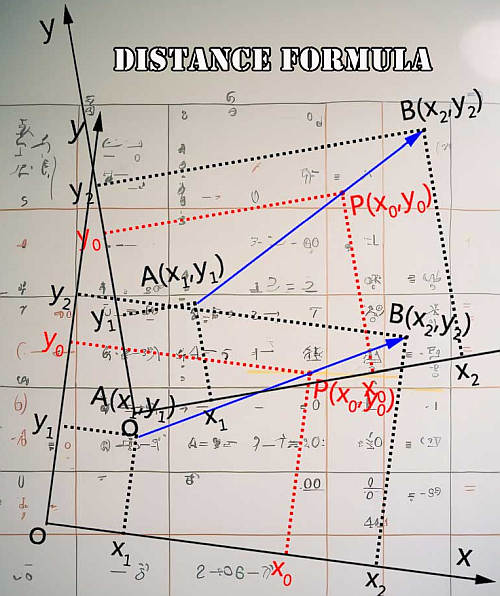
Innanzitutto occorre ricordare che il distanza tra due punti nel piano euclideo si basa sul concetto dei principi geometrici di base che consentono di utilizzare il teorema di Pitagora.

Come si calcola il punto medio?

Concettualmente parlando, il punto medio è il punto che è a metà strada tra i due punti. Questa idea di metà strada è in linea con i teoremi geometrici di proporzionalità.

Il punto medio è una coppia ordinata che si trova a metà strada tra due punti dati. Questa è la prima cosa che devi sapere: alcune persone pensano erroneamente a una quantità come al punto medio, e in realtà quello che stai cercando di ottenere è una coppia ordinata.

Il punto medio dei punti indicati \((x_1, y_1)\) e \((x_2, y_2)\) è dato dalla seguente formula:

\[ \left( x_M, y_M \right) = \displaystyle \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right) \]

Spiegazione della formula del punto medio

Definizione Della Formula: La formula del punto medio sopra è strettamente correlata a formula della distanza . In effetti, ciò che fa la formula sopra è semplicemente prendere la media delle due coordinate corrispondenti.

Cioè, la prima coordinata del punto medio è la media delle prime coordinate dei due punti dati, e la seconda coordinata del punto medio è la media delle seconde coordinate dei due punti dati. Come utilizzare la formula sopra? Si prega di controllare gli esempi seguenti.

Per cosa utilizzo la formula del punto medio?

L'idea di punto medio ci è così familiare perché è strettamente associata all'idea di "metà strada" da un punto all'altro. Tali situazioni sono molto comuni nella vita reale, dove potremmo essere interessati a dividere qualcosa, ad esempio.

Naturalmente, il processo di divisione di qualcosa non deve necessariamente coinvolgere un punto medio, ma di solito lo farà quando si esegue una divisione uguale.

Quindi, la formula del punto medio è così utile in parte perché è un modo per farlo utilizzando la formula della distanza in un caso molto particolare, in cui il punto che stiamo trovando è alla stessa distanza da entrambi i punti indicati.

Esempi di formule del punto medio

Supponiamo di avere due punti \((1, 3)\) e \((4, 8)\), quindi la formula del punto medio viene calcolata come segue:

\[ \left( x_M, y_M \right) = \displaystyle \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right) = \left( \frac{1 + 4}{2}, \frac{3+ 8}{2} \right) = \left( \frac{5}{2}, \frac{11}{2} \right) \]

A volte lasci la risposta come frazione, altre volte ti viene chiesto di calcolare la risposta con i decimali, nel qual caso il punto medio sarebbe (2,5, 5,5) nell'esempio precedente.

Altri esempi di punto medio

Come gestire la formula del punto medio con le frazioni? È la stessa procedura. Supponiamo di avere due punti \((\frac{1}{2}, \frac{1}{4})\) e \((\frac{3}{5}, \frac{3}{4})\), quindi il punto medio viene calcolato come:

\[ \left( x_M, y_M \right) = \displaystyle \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right) = \left( \frac{1/2 + 3/5}{2}, \frac{1/4+ 3/4}{2} \right) = \left( \frac{11/10}{2}, \frac{1}{2} \right) = \left( \frac{11}{20}, \frac{1}{2} \right) \]

Questo ha qualcosa a che fare con pitagora

Quasi tutto ha a che fare con Pitagora . Il punto medio dell'ipotenusa si proietterà al punto medio dei cateti di un triangolo rettangolo. Inoltre, puoi prendere i due punti e calcolare il distanza tra loro , utilizzando la formula pitagorica.